Questions
INSTRUCTIONS TO CANDIDATES
- This paper consists of two sections: Section I and Section II.
- Answer ALL questions in section 1 and ONLY FIVE questions from section II
- All answers and workings must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculation, giving your answer at each stage in the spaces below each question.
- Non – Programmable silent electronic calculators and KNEC mathematical tables may be used, except where stated otherwise.
Section I (50 marks)
Answer All the questions in this section
- Evaluate without using tables or calculator. (3 marks)
¼ of 2 + 3 ¾ ÷ ³/₈ - 4 ½ x 3¹/₃
2 ⁴/₅ x 1³/₇ - 4 ÷ ²/₃ + ³/₅ of 15 - Simplify: . (3 marks)
2 - 10x + 12x²
36x² + 3 - 21x - A tourist arrived in Kenya with US Dollars 3000 which he exchanged into Kenya shillings. He spent Ksh. 75000 on hotel accommodation and Ksh.42500 on travel and other expenses. He changed the remaining money into sterling pounds. Calculate how much money in sterling pounds that he remained with using the following rates. (Leave your answer to the nearest 1£)
(4marks)Buying(Kshs) Selling(Kshs) 1 US dollar($) 78.45 78.95 1 Sterling pound(£) 120.27 121.04 - Solve for y in the equation 8 (2y – 1) x 32y = 16 (y + 1). (3marks)
- Solve the equation: (3marks)
1(x+3)+ x)= 11
x (x+3) 28x - Determine the equation of the normal to the curve y = 3x2 – 4x + 1 at the point (2, 5). (3marks)
- Given that AB =m
and CD =
are parallel, find the value of K and hence evaluate |CD| (3marks)
- Make a the subject of the formula:
x = y +√(x2+ a2) (3marks) - Find the equation of a straight line which is equidistant from the points A(2, 3) and B(6, 1). Express your answer in the form x/a+ y/b = 1 where a and b are constant. (3marks)
- The GCD and LCM of three numbers are 3 and 1008 respectively. If two of the numbers are 48 and 72 respectively, find the least possible value of the third number. (3 marks)
- Kamau salary increased from Ksh 16,800 to 18,800 in the month of April. State the ratio in which it changed. What was the percentage change in his salary? Leave you percentage answer to 4. s. figures. (3marks)
- If tan X = 4/3 , find the value of sin2X + cos X without using tables or calculator. (3marks)
- The area of a rhombus is 60cm2. Given that one of its diagonal is 15cm long. Calculate the perimeter of the rhombus. (3 marks)
- If x is an integer find all the integral values of x given that: (3marks)
-3 < 2x + 4 < -3x + 9 - Solve for x in log3 (4 + 3x) + 3log33 – 2 = log3(x + 6) (3marks)
- The sum of interior angles of two regular polygons of sides, n-1 and n are in the ratio 2:3. Calculate
- The value of n. (2 marks)
- The interior angle of each polygon. (2 marks)
SECTION II (50 MARKS)
Answer any five questions in this section
-
- A train of length 100m travelling at 12 m/s passes a second train of length 140m travelling in the same direction at a speed of 9 m/s. Calculate the time taken for the train to pass completely. (3 marks)
- X and Y cycle to school 10 km away. X cycles at 1.5 km/h faster than Y and arrives 10 minutes before Y. Determine the speeds at which the two cycle. (4 marks)
- A train leaves town A and travels towards B at 48 km/h. At the same time, another train leaves town B and travels towards A at a speed of 52 km/h. If the two towns are 500 km apart, find how far apart the trains are after traveling for 45 minutes. (3 marks)
- A curve whose equation is 2y = 6-12x+9x2- 2x3 turns at points A and B.
- Find the coordinates of A and B (5marks)
- Determine the nature of points A and B (3marks)
- Sketch the curve (2marks)
- Income tax is charged on annual income at the rate shown below.
Mr. Sang earn a basic salary of Ksh.15,000 per month and lives in a company house for which he pays nominal rent of Ksh.1250 per month. He enjoys personal relief of Ksh.1056 per month and insurance relief of Ksh.270 per month.Taxable income K£p.a Rate Ksh/£. 1-2300 2 2301- 4600 3 4601- 6900 5 6901- 9200 7 9201- 11500 9 11501 and over 10
Calculate;- His taxable income in K£.p.a. (3 marks)
- The amount of tax he pays per month in Kenya shillings. (5 marks)
- His net monthly salary in shillings. (2 marks)
- The frequency distribution table below shows the marks scored by 117 form four candidates of Kaptata High School.
Marks 10-19 20-29 30-39 40-49 50-59 60-69 70-79 No. of students 13 14 18 20 23 17 12 - Draw a cumulative frequency curve of the distribution. (5marks)
- Use you graph to determine:
- The median (2 marks)
- Quartile deviation (3 marks)
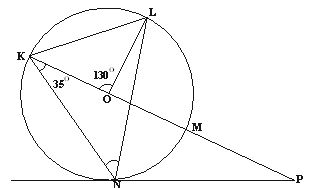
- In the diagram below KNML is a circle centre O. PN is a tangent to the circle at N. KOMP is a straight line, angle NKM = 350 and angle KOL = 1300
Giving reasons find:- Angle MLN (2 marks)
- Angle KLM (2 marks)
- Angle OLN (2 marks)
- Angle LNP (2 marks)
- Angle MPN (2 marks)
- A car whose initial value is Ksh 600,000 depreciates at a rate of 12% p.a. Determine:
- Its value after 5 years. (4 mks)
- Its value of depreciation after 5 years. (2 mks)
- The number of year it will take for the value of the car to be Ksh 300,000 (4 mks
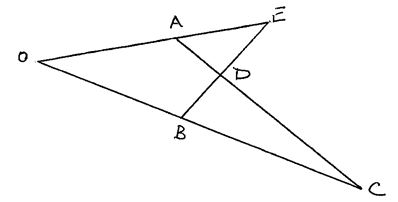
- In the figure below OE = a , OB = b, OA : AE = 2 : 3 and OC : BC = 2 : 1
- Express AC and BE in terms of a and b. (2 marks)
- DC and kAC and BD = hBE. Determine the values of k and h by expressing DC in two ways. (6 marks)
- Find the ratio of AD: DC. (2 marks)
- A theatre has seating capacity of 250 people. The charges are shs. 100 for ordinary seat and shs 160 for special seat. It cost shs 16000 to stage a show and the theatre must make a profit. There are never more than 200 ordinary seats and for a show to take place,at least 50 ordinary seats must be occupied; the number of special seats is always less than twice the number of ordinary seats.
- Taking X to be number of ordinary seats and y to be the number of special seats, write down all the inequalities representing the above information (2 marks)
- On the grid provided, draw a graph to show the inequalities in (a) above (4marks)
- Determine the number of seats of each type that should be booked in order to maximize the profit ( 2 marks)
- Calculate this maximum profit ( 2marks)
Marking Scheme
- Num
4/8 + 15/4 x 8/3 - 9/2 x 10/3
4/8 + 10 - 15
Denom
2 ⁴/₅ x 1³/₇ - 4 ÷ ²/₃ + ³/₅ of 15
14/5 x 10/7 - 4 x 3/2 + 9
4 - 6 + 9
10.5 - 15
7
= 4.5 = 9/14
7 - 2 - 10x + 12x²
36x² + 3 - 21x
Num:
2(3x-1)(2x-1)
3(3x-1)(4x-1)
= 2(2x-1) or 4x-2
3(4x-1) 12x -3 - 3000 USD = Ksh 3000 x 76.45= 235350
reminder = 235350 - (7500 + 4200)
= Ksh 117850
= 117850 = 973.65
121.04
= 974 - 8 (2y – 1) x 32y = 16 (y + 1)
23 (2y – 1) x 25y = 24 (y + 1)
6y - 3 + 5y = 4y + 4
7y=7
y=1 - 1(x+3)+ x)= 11
x (x+3) 28x
2x+ 3 = 11
x2 + 3x 28x
28x(2x+3) = 11(x2 + 3x)
56x2 + 84x = 11x2 + 33x
56x2 - 11x2 + 84x - 33x = 0
45x2 + 51x=0
x(45x + 51)=0
x= 0
45x = -51
x= -51/45
x = - 1 2/15 - dy/dx = 6x-4
M1 = 12-4=8
M2 = -1/8
y-5 = -1
x-2 8
8y -40 = -x + 2
8y = -x + 42 - 5m = 15
m= 3
a= k-1
k=10
CD = √(a2 + 152) = 17.49 - √(x2 + a2)= x -y
x2 + a2 = (x-y)2
a2 = (x-y)2 - x2
a = ± √(x-y)2 - x2 - Mid point (4,2)
m1= 1-3 = -1
6-2 2
m2 = 2
y-2 = 2/7
x-4
x/3 + y/6 = 1 - LCM of 48 and 72
= 24 x 32 = 144
3rd No = 3 x 1008
144
=21 - 16800: 18800
168 : 188
41:47
% exchange = 18800 -16800= 2000
= 2000 x 100
16800
= 11.90% - Sin x = 4/5
Cos x = 3/5
Sin 2 x + Cos x = (4/5)2 + (3/5)
= 31/25 = 1 6/25 - 1/2 x 15 x h x 2 = 60
h=4
x2 = 42 + 7.52
x = 8.5
8.5 x 4= 34 - -3<2x + 4 < -3x + 9
-7<2x
-3.5< x
2x + 4 < -3x + 9
5x < 5
x < 1
Integral Values -3, -2, -1, 0 - Log 3 (4 + 3x)(27) = 2
x + 6
9(x+ 6)= 27(4+3x)
x+6 = 12 + 9x
8x = -6
x = -3/4 -
- (2(n-1) - 4)90 : (2n-4)90 = 2:3
(2n - 6): (2n-4)= 2:3
2n - 6 = 2
2n - 4 3
6n - 18 = 4n - 8
2n = 10
n = 5 - ex = 360/5 = 72
ex = 360/4 = 90
interior angles ⇒ 108°, 90°
- (2(n-1) - 4)90 : (2n-4)90 = 2:3
-
- R.S = 12 - a = 3
240/3 = 80 sec - 10/x - 10/x + 1.5 = 1/6
90 = x2 + 1.5x
x2 + 3x - 180 = 0
x2 + 15x - 12x - 180 = 0
x(x+15) - 12(x + 15)= 0
(x+ 15)(x - 12) = 0
x = -15 or x = 12
x = 12
y= 12 km/hr
x = 13.5km/hr - T1 = 48 x 3/4 = 36
T2 = 52 x 3/4 = 39
D = 500 - (36 + 39)
= 425
- R.S = 12 - a = 3
-
- y = 3 - 6x + 4.5x2 - 1 x 8
dy/dx = -6 + 9x - 3x2 = 0
3x2 - 9x + 6 = 0
(x-1)(x-2)= 0
x=1 or x=2
coordinates of A(1, 0.5) B (2, 1) - d²y = a - 6x ,
dx2
when x = 1
d²y = 3
dx2
A(1, 0.5) minimum
When x = 2 d²y = -3
dx2
B(2, 1)maximum -
- y = 3 - 6x + 4.5x2 - 1 x 8
-
- 115/100 x 15000 - 1250
= 16000 x 12 = 9600
20 - 1st slab = 2300 x 2 = 4600
2nd = 2300 x 3 = 6900
3rd slab = 2300 x 5= 11500
4th slab = 2300 x 7 = 16100
5th slab = 400 x 9 = 3600
Tital tax = 42700
p.m = 42700 ÷ 12 = 3558.30
3558.30 - 1226.00 = 2332.30 - 15000 - 2330. 30
= 12767.70
- 115/100 x 15000 - 1250
-
- CF = 13, 27, 45, 65, 38, 105, 117
Plotting p2
Scale - S1
Curve - C1 -
- From the graph
The reading = 46.5 - a1= 31
a3= 59.5
quartile deviation
59.5 - 31
2
= 14.25
- From the graph
- CF = 13, 27, 45, 65, 38, 105, 117
-
- <MLN = 35°
Angles subtended by the same chord at the circumference - <KLM = 90°
Diameter substend an angle of 90° at the circumference - <OLM=30°
Opposite angles at a cyclic quadrant - <LNP = 60°
Radius and tangent intersect at 90° - <MPN = 60°
Sum of interior angles in a triangle.
- <MLN = 35°
-
- A= 600,000 (1 - 12/100)5
= 600,000(0.85)5
= 316, 620 - 600,000 - 316620 = 283380
- 300,000 = 600,000 (1 - 12/100)h
0.88h = 0.5
n = Log 5
log 0.88
n = 5.422
- A= 600,000 (1 - 12/100)5
-
- AC = a + 2b
BE = -b + 5/3b - DC = K(-a + 2b)
= -Ka + 2Kb
BD = n (-b + 5/3a)
= -hb + 5/3ha
DC = DB + BC
= hb - 5/3ha + b
=b (h+1)- 5/3ha
5/3h = k
1+h = 2k
1+h = 2(5/3h)
10h = 3 + 3h
7h= 3
h = 3/7
k = 5/3 x 3/7 = 5/7
DC= 5/7AC ⇒ DC: AC = 5:7
AD:DC = 2:5
- AC = a + 2b
-
- x + y < 250
x< 200
x> 50
y < 2x
y>0 - From the graph
ordinary 84
Special 166 - Maximum profit
84 x 100 + 166 x 160
= 34960
- x + y < 250
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - 2021 KCSE Eldoret Diocese Mock Exams.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students