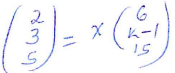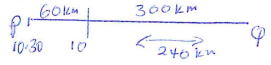- The paper consists of TWO sections: Section I and Section II.
- Answer ALL questions in Section I and ONLY five from Section II.
- All answers and working must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculations, giving your answers at each stage in the spaces below each question
- Marks may be given for correct working even if the answer is wrong.
- Non – programmable silent calculators and KNEC Mathematical tables may be used except where stated otherwise.
SECTION I (50 MARKS)
Answer all the questions in the space provided below each question
- Evaluate without using mathematical tables or calculator (3marks)
−12 ÷ 4 −6 × 3 + 5 × 2
8 + (−5) ÷2 × (−4) - A three-digit number is such that twice the hundreds digit is more than the tens digit by 2.the unit digit is thrice the hundred digit. When the digits are reversed, the number is increased by 594.Find the number. (4marks)
- Simplify (3marks)
x + 4 − 5x + 20
x−4 x2 −16 - The mass of maize flour to the nearest 10 grams is 8. 67kg.Determine the percentage error in this measurement. (3marks)
- Without using a calculator, solve for x in the equation 0.5x x 0.1251−x = 32. (3marks)
- The velocity V m/s of a particle in motion is given by V = 3t2 − 2t + 5.Calculate the distance travelled by the particle between t= 2 seconds and t = 6 seconds. (3 marks)
- Given that, the coordinates of two points P and Q are (2, 3, 5) and (6, k−1, 15) respectively and that their position vectors are parallel, Calculate the value of IPQI. (4marks)
- A dealer sells a mobile phone at a profit of 25%. The customer sells it to a friend at ksh 60,000, making a profit of 20 %. Find the cost prize of the mobile phone. (3 marks)
- A wall clock that gains 20 seconds after every hour was set to read the correct time on Tuesday at 03 25. Determine the time the wall clock will read on Thursday 03 25 h. (3 marks)
- A cylinder of radius 15 cm and height 24 cm is filled with water. A solid hemisphere of radius 7cm is submerged into the cylinder and removed. Find the change in height of water level in the cylinder. (4 marks)
- The average rate of depreciation in value of a laptop is 10% per annum. After three complete years its value was ksh 35,000. Determine its value at the start of the three-year period. (3marks)
- If 3x+2y : 7x − y = 3:2,calculate the ratio x:y (3marks)
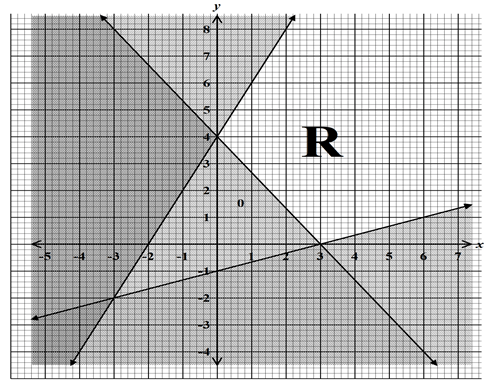
- State the inequalities that satisfy the region defined by R. (3marks)
- Solve for θ in the equation sin(2θ + 30)° = tan45° (3marks)
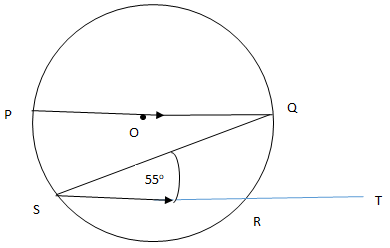
cos(3θ−40)° - The figure below shows a circle PQRS Centre O with SR produced to T.PQ//SR and ∠QSR=55°.Calculate the size of∠QRT. (3 marks)
- The scale of a map is 1: 200.Calculate the actual area of a triangular coffee field whose sides are 6cm, 8cm and 10cm on the map. (3 marks)
SECTION II (50 MARKS)
Answer only five questions from this section.
- A tower is on a bearing of 030° from a point P and a distance of 100m.From P, the angle of elevation of the top of the tower is 15° and the angle of depression of the foot of the tower is 1°.
- Calculate the height of the tower. (4 marks)
- A point Q is on the same horizontal plane as point P. The tower is on a bearing of 330° from Q and a distance of 70 m. Calculate:
- The distance from P to Q. (3 marks)
- The bearing of P from Q. (3 marks)
-
- The diagram below shows a bucket in the shape of a frustum of a cone with diameters 36 cm and 24 cm and a vertical height of 28 cm. The bucket contains water such that the diameter of the water surface is 30cm. Calculate the volume of the bucket. (6 marks)
- If the bucket above has a hole and 1.1 cm3 of water leaks out every 5 seconds and collects in a cylindrical can of base radius and height 10 cm and 25 cm respectively. Calculate how long it takes to fill the cylindrical can. (4 marks)
- The diagram below shows a bucket in the shape of a frustum of a cone with diameters 36 cm and 24 cm and a vertical height of 28 cm. The bucket contains water such that the diameter of the water surface is 30cm. Calculate the volume of the bucket. (6 marks)
- A piece of wire, 18 cm long is cut into two parts. The first part is bent to form the four sides of a rectangle having length x cm and breath 1 cm.
- State two expressions in terms of x only for the perimeter of the square and the rectangle. (2 marks)
- If the sum of the areas of the square and the rectangle is A cm2, show that A = 16 − 3x + x² (2 marks)
4 - If A =8cm2, Solve the equation in (b) above for x, hence find the possible dimensions of the two pieces of wire. (6 marks)
- The distance between two towns P and Q is 300 km. A bus started at P at 10.30 am and travelled towards town Q at 80 km/h. After 45 minutes a car started at Q and travelled to town P at x km/h. The car met the bus after 1hour 20 minutes.
- Determine the value of x. (3 marks)
- Find the distance from P where the car met the bus. (2 marks)
- At what time did the car meet the bus? (2 marks)
- If t a shuttle started at P, 1hour after the car left Q for P. Calculate the speed to the nearest km/h at which the shuttle should be driven in order to arrive at Q at the same time with the bus. (3 marks)
-
- Complete the table of values for the equation y = x2 + 3x − 6, given that −6 ≤ x ≤ 4. (2marks)
x −6 −5 −4 −3 −2 −1 0 1 2 3 4 y 12 −6 −6 22 - Using a scale of 1cm to represent 2 units in both axes, draw the graph of y = x2 +3x − 6 . (3 marks)
- Using the graph drawn above Solve the equation
- x2 + 3x − 6 = 0 (2 marks)
- x2 + 3x − 2 = 0 (3 marks)
- Complete the table of values for the equation y = x2 + 3x − 6, given that −6 ≤ x ≤ 4. (2marks)
- A Business man is paid a commission of 5% on sales of goods worth over ksh 100,000. He is paid a monthly salary of ksh 15,000 but 2% of his total earning is remitted as tax. In a certain month he sold goods worthy khs 500,000.
- Calculate his monthly net earnings that month. (5marks)
- The following month, his monthly salary increased by 20%. His commission was increased to 10% but on goods worth over ksh 200,000. If his total earnings that month was ksh 64,800, Calculate the money received from the sale of goods. (5marks)
- The coordinates of two points A and B are (2, −3) and (−4, 5) and R is the mid-point of AB.
- Determine the coordinates of R. (2 marks)
- Find the equation of a straight line joining A and B, expressing it in the form y = mx + c where m and c are constants. (3 marks)
- The straight line L1 which is a perpendicular bisector of AB meets the X-axis at T. Find the coordinates of T. (3 marks)
- If the straight line L1 is parallel to a line that passes through the point (−1, 6) and (a, 8), find a. (2 marks)
- Two inlet taps P and Q opened at the same time can fill a tank in 2½ h. The two taps were opened together at the same time and after 1 hour 10 minutes tap Q was closed and P continued alone and filled the tank after a further 4 hours. Find:
- The fraction of the tank filled by both taps for 1 hour. (1 marks)
- The fraction of the tank filled by tap P after Q was closed. (2 marks)
- The time which each tap working alone would have taken to fill the tank. (7 marks)

MARKING SCHEME
SECTION I (50 MARKS)
Answer all the questions in the space provided below each question
- Evaluate without using mathematical tables or calculator (3marks)
−12 ÷ 4 −6 × 3 + 5 × 2
8 + (−5) ÷2 × (−4)
Num −3 −18 + 10 = −11
Deno 8 −5 × −4
2
8 + 10 = 18
= −11
18 - A three-digit number is such that twice the hundreds digit is more than the tens digit by 2.the unit digit is thrice the hundred digit. When the digits are reversed, the number is increased by 594.Find the number. (4marks)
xyz = 100x + 10y + z
2x = y + 2
z = 3x
zyx = 100z + 10y + x
100x + 10y + z = 100z + 10y + y − 594
99x − 99z = −594
x − z = −6
z = 3x
2y = y + 2
2x = y+ 2
x − 3x = −6
−2x = −6
x = 3
z = 9
6 = y + 2
4 = y
= 349 - Simplify (3marks)
x + 4 − 5x + 20
x−4 x2 −16
(x + 4)(x+ 4) − 5x − 20
(x−4)(x + 4)
x² + 8x +16 − 5x −20
( x − 4) ( x + 4)
x² + 8x + 16 − 5x −20
(x − 4) (x + 4)
x² + 3x −4
(x − 4)(x + 4)
x² + 4x − x − 4
(x − 4)(x + 4)
x(x + 4) −1(x + 4)
(x−4) (x + 4)
(x−1) (x + 4)
(x−4) (x + 4)
(x − 1)
(x + 4 - The mass of maize flour to the nearest 10 grams is 8. 67kg.Determine the percentage error in this measurement. (3marks)
Error = ½ × 10 = 5gm
= 0.005kg
%error = 0.005 × 100
8.67
= 0.05767% - Without using a calculator, solve for x in the equation 0.5x x 0.1251−x = 32. (3marks)
(½)x + (1/8)1−x = 25
2−x + 2−3(1−x) = 25
−x + −3 + 3x = 5
2x − 3 = 5
2x = 8
x = 4 - The velocity V m/s of a particle in motion is given by V = 3t2 − 2t + 5.Calculate the distance travelled by the particle between t= 2 seconds and t = 6 seconds. (3 marks)
(216 − 36 + 30) − (8 − 4 + 10)
210 − 14
= 196 - Given that, the coordinates of two points P and Q are (2, 3, 5) and (6, k−1, 15) respectively and that their position vectors are parallel, Calculate the value of IPQI. (4marks)
2 = 6x
1/3 = x
3 = 1/3(k − 1)
9 = k − 1
10 = k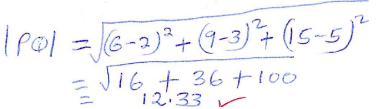
- A dealer sells a mobile phone at a profit of 25%. The customer sells it to a friend at ksh 60,000, making a profit of 20 %. Find the cost prize of the mobile phone. (3 marks)
120% → 60,000
100% → 100 × 60,000
120
= 50,000
125% → 50,000
100% → 100 × 50,000
125
= 40,000 - A wall clock that gains 20 seconds after every hour was set to read the correct time on Tuesday at 03 25. Determine the time the wall clock will read on Thursday 03 25 h. (3 marks)
1hr → 20seconds
48hrs → 48 × 20
= 960seconds
960
60
= 16minutes
3 25
+ 16
3 41
= 0341h - A cylinder of radius 15 cm and height 24 cm is filled with water. A solid hemisphere of radius 7cm is submerged into the cylinder and removed. Find the change in height of water level in the cylinder. (4 marks)
V = 22/7 × 152 × 24
= 16971
4/3 × ½ × 22/7 × 49 × 7
= 718.7
16971 − 718.7
= 16252.3
22/7 × 152 × h = 16252.3
h = 22.98
Change in height
= 24 − 22.98
= 1.017 - The average rate of depreciation in value of a laptop is 10% per annum. After three complete years its value was ksh 35,000. Determine its value at the start of the three-year period. (3marks)
x(1 − 10/100)3 = 35,000
(0.9)3x = 35,000
x = 35,000
0.729
= 48010.97 ≈ 48011 - If 3x+2y : 7x − y = 3:2,calculate the ratio x:y (3marks)
3x+2y = 3/2
7x − y
2(3x + 2y) = 3(7x − y)
6x + 4y = 21x − 3y
7y = 15x
15x = 7y
x/y = 7/15
x:y = 7:15 - State the inequalities that satisfy the region defined by R. (3marks)

x/3 + y/4 = 1
x/3 + y/4 ≥ 1
4x + 3y ≥ 12
x/−2 + y/4 = 1
−2x + y = 4
−2x + y < 4
x/3 + y/−1 = 1
x − 3y ≤ 3 - Solve for θ in the equation sin(2θ + 30)° = tan 45° (3marks)
cos(3θ−40)°
sin(2θ + 30)° = cos(3θ − 40)°
2θ + 30 = 90 − (3θ − 40)
2θ + 30 = 90 − 3θ − 40
5θ = 100
θ = 20° - The figure below shows a circle PQRS Centre O with SR produced to T.PQ//SR and ∠QSR=55°.Calculate the size of∠QRT. (3 marks)
∠ PQS = ∠ QSR alternate angles are equal
∠ PSQ = 90° Diameter subtends 90° at circumference
∠ QPS = 90 − 55 = 35°
∠ QPS = ∠QRT = 35° exterior angle is equal to interior opposite angle in a cyclic quadrilateral - The scale of a map is 1: 200.Calculate the actual area of a triangular coffee field whose sides are 6cm, 8cm and 10cm on the map. (3 marks)
1cm rep 2m
1cm2 rep 4m2
½ × 6 × 8 = 24cm2
1cm2 rep 4m2
24cm2 rep 24 × 4
1
= 96
SECTION II (50 MARKS)
Answer only five questions from this section.
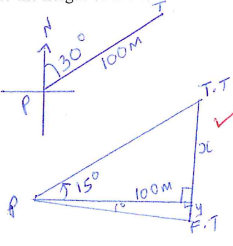
- A tower is on a bearing of 030° from a point P and a distance of 100m.From P, the angle of elevation of the top of the tower is 15° and the angle of depression of the foot of the tower is 1°.
- Calculate the height of the tower. (4 marks)
tan 15 = x/100
x = 26.79m
tan 1° = y/100
y = 1.746m
26.79 + 1.746
= 28.536 ≈ 28.54 - A point Q is on the same horizontal plane as point P. The tower is on a bearing of 330° from Q and a distance of 70 m. Calculate:
- The distance from P to Q. (3 marks)
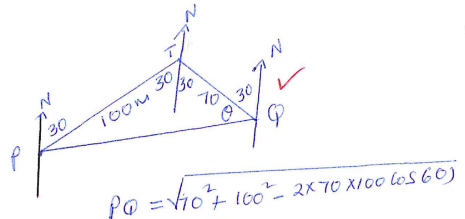
= √7900
= 88.88 - The bearing of P from Q. (3 marks)
100 = 88.88
sinθ sin 60
sin θ = 100 × sin 60
88.88
sin θ = 0.9744
θ = 77.00°
360 − (30+77)
360 − 107
= 253°
- The distance from P to Q. (3 marks)
- Calculate the height of the tower. (4 marks)
-
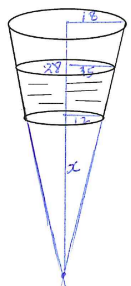
- The diagram below shows a bucket in the shape of a frustum of a cone with diameters 36 cm and 24 cm and a vertical height of 28 cm. The bucket contains water such that the diameter of the water surface is 30cm. Calculate the volume of the bucket. (6 marks)
28 + x = 18
x 12
28 + x = 1.5
x 1
1.5x = 28 + x
0.5x = 28
x = 56
1/3 × 22/7 ×182 × 84 − 1/3 × 22/7 ×122 × 56
28,512 − 8,448
= 20,064 - If the bucket above has a hole and 1.1 cm3 of water leaks out every 5 seconds and collects in a cylindrical can of base radius and height 10 cm and 25 cm respectively. Calculate how long it takes to fill the cylindrical can. (4 marks)
22/7 × 102 × 25
= 7857
5 second → 1.1cm3
? → 7857
7857 × 5
1.1
35713.6 seconds
35713.6
3600
= 9.920
9hrs 55minutes
- The diagram below shows a bucket in the shape of a frustum of a cone with diameters 36 cm and 24 cm and a vertical height of 28 cm. The bucket contains water such that the diameter of the water surface is 30cm. Calculate the volume of the bucket. (6 marks)
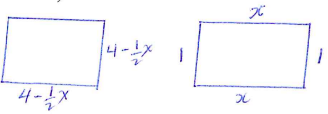
- A piece of wire, 18 cm long is cut into two parts. The first part is bent to form the four sides of a rectangle having length x cm and breath 1 cm.
- State two expressions in terms of x only for the perimeter of the square and the rectangle. (2 marks)
P = (4−½x)4
P = 16 − 2x
P = 2x + 2 - If the sum of the areas of the square and the rectangle is A cm2, show that A = 16 − 3x + x² (2 marks)
4
A = (4 − ½x) (4 − ½x + x
A = 16 − 4x + ¼x2 + x
A = 16 − 3x + ¼x2 - If A =8cm2, Solve the equation in (b) above for x, hence find the possible dimensions of the two pieces of wire. (6 marks)
16 − 3x + ¼x2 = 8
8 − 3x + ¼x2 = 0
x2 − 12x + 32 = 0
x = 12 ± √(144 − 128)
2
x = 12 ± 4
2
x = 8 or 4
x = 4, 8 impossible
16−8 2×4+2
8 10
- State two expressions in terms of x only for the perimeter of the square and the rectangle. (2 marks)
- The distance between two towns P and Q is 300 km. A bus started at P at 10.30 am and travelled towards town Q at 80 km/h. After 45 minutes a car started at Q and travelled to town P at x km/h. The car met the bus after 1hour 20 minutes.
- Determine the value of x. (3 marks)
45/60 × 80 = 60km
R.S = x + 80
240 = 4
x+60 3
720 = 4x + 240
4x = 480
x = 120 - Find the distance from P where the car met the bus. (2 marks)
4/3 × 120 = 160km
300 − 160 = 140km - At what time did the car meet the bus? (2 marks)
10.30
+ 45
11.15
+ 1.20
12.35p.m - If t a shuttle started at P, 1hour after the car left Q for P. Calculate the speed to the nearest km/h at which the shuttle should be driven in order to arrive at Q at the same time with the bus. (3 marks)
45/60 × 80 + 1 × 80
60 + 80 = 140
160 = 300
80 y
160y = 300 × 80
y = 300 × 80
160
= 150 km/h
- Determine the value of x. (3 marks)
-
- Complete the table of values for the equation y = x2 + 3x − 6, given that −6 ≤ x ≤ 4. (2marks)
x −6 −5 −4 −3 −2 −1 0 1 2 3 4 y 12 4 −2 −6 −8 −8 −6 −2 4 12 22 - Using a scale of 1cm to represent 2 units in both axes, draw the graph of y = x2 +3x − 6 . (3 marks)

- Using the graph drawn above Solve the equation
- x2 + 3x − 6 = 0 (2 marks)
x = 1.4 or −4.4 - x2 + 3x − 2 = 0 (3 marks)
x2 + 3x − 6 = y
−4 = y
at point of intersection
x = −3.5 or 0.6
- x2 + 3x − 6 = 0 (2 marks)
- Complete the table of values for the equation y = x2 + 3x − 6, given that −6 ≤ x ≤ 4. (2marks)
- A Business man is paid a commission of 5% on sales of goods worth over ksh 100,000. He is paid a monthly salary of ksh 15,000 but 2% of his total earning is remitted as tax. In a certain month he sold goods worthy khs 500,000.
- Calculate his monthly net earnings that month. (5marks)
5/100 × 400,000 = 25,000
Total earnings = 15000+25000
= 40,000
tax = 2/100 × 40000
= 800
Net earnings = 40000 − 800
= 39,200 - The following month, his monthly salary increased by 20%. His commission was increased to 10% but on goods worth over ksh 200,000. If his total earnings that month was ksh 64,800, Calculate the money received from the sale of goods. (5marks)
120/100 × 15000 = 18000
10/100 × x = 0.1x
2/100(10/100x + 18000)
0.02 (0.1x + 18000)
0.002x + 360
(0.1x + 18,000) − (0.002x + 360) = 64800
0.098x + 17640 = 64800
0.098x = 47160
x = 481,224
Total = 481,224 + 200,000
= 681,224
- Calculate his monthly net earnings that month. (5marks)
- The coordinates of two points A and B are (2, −3) and (−4, 5) and R is the mid-point of AB.
- Determine the coordinates of R. (2 marks)
(2+−4 , −3+5)
2 2
R(−1, 1) - Find the equation of a straight line joining A and B, expressing it in the form y = mx + c where m and c are constants. (3 marks)
Grad = 5−−3 = 8 = −4
−4−2 −6 3
y − 5 = −4
x + 4 3
3(y−5) = −4(x+4)
3y − 15 = −4x −16
3y = −4x + 1
y = −4x + 1
3 3 - The straight line L1 which is a perpendicular bisector of AB meets the X-axis at T. Find the coordinates of T. (3 marks)
G1 = −4/3
G2 = 3/4
y−1 = ¾
x+1
3(x+1) = 4(y−1)
3x + 3 = 4y − 4
3x + 7 = 4y
4y = 3x + 7
T(k,0)
4y = 7
y = 7/4
y = 1¾
T(1¾,0) - If the straight line L1 is parallel to a line that passes through the point (−1, 6) and (a, 8), find a. (2 marks)
G1 = 3/4
¾ = 8−6
a+1
3/4 = 2
a+1
8 = 3(a+1)
8 = 3a + 3
5 = 3a
a = 5/3
=12/3
- Determine the coordinates of R. (2 marks)
- Two inlet taps P and Q opened at the same time can fill a tank in 2½ h. The two taps were opened together at the same time and after 1 hour 10 minutes tap Q was closed and P continued alone and filled the tank after a further 4 hours. Find:
- The fraction of the tank filled by both taps for 1 hour. (1 marks)
5/2hrs → full tank
1hr → 1 × 1/1 ÷ 5/2 = 1 × 1 × 2/5 = 2/5 - The fraction of the tank filled by tap P after Q was closed. (2 marks)
1hr → 2/5
11/6hrs → 2/5 × 7/6 × 1 = 7/15
Remaining 1 − 7/15 = 8/15 - The time which each tap working alone would have taken to fill the tank. (7 marks)
P
4hrs → 8/15
1hr → 8/15
1hr → 2/15
→ 15/15
15/15 × 1 ÷ 2/15
15/15 × 1 × 15/2 = 7.5hrs
let rate of working for Q be y
2/15 + y = 2/5
y = 2/5 − 2/15
y = 6 − 2
15
y = 4/15
1hr → 4/15
? → 15/15
15/15 × 1 × 15/4
= 15/4
= 3¾hrs
- The fraction of the tank filled by both taps for 1 hour. (1 marks)
Download Mathematics Paper 1 Questions and Answers - Baringo North Joint Evaluation Mock Exams 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students