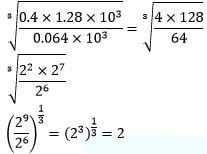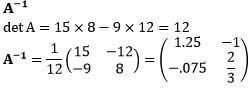INSTRUCTIONS TO CANDIDATES
- Write your name and index number in the spaces provided at the top of this page.
- Write your school name, sign and write the date of the examination in the spaces provided above.
- This paper consists of Two sections: Section I and Section II
- Answer ALL questions in Section I and any five questions from Section II
- Show all the steps in your calculations, giving your answers at each stage in the spaces provided below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non-Programmable silent electronic calculators and KNEC Mathematical Tables may be used.
- Candidates should check the question paper to ensure that all the pages are printed as indicated and no questions are missing.
- Candidates should answer the questions in English.
For Examiners’ Use Only
SECTION I
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Total |
SECTION II
|
|
|
|
|
|
|
Total |
Grand Total |
||||
|
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
QUESTIONS
SECTION I (50 Marks)
Answer all the questions in this section
- Without using mathematical tables or a calculator, evaluate: (3 marks)
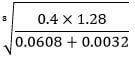
- Find the exact value of 2.3 ̇4 ̇-1.9 ̇1 ̇ (4 marks)
- The HCF and GCD of three numbers are 7920 and 12 respectively. Two of the numbers are 48 and 264. Using factor notation, find the third number if one of its factors is 32. (3 marks)
- The graph below (not drawn to scale) is a plot for the function y=ax2+bx+k where a, b and k are constants.
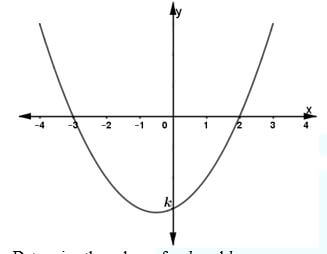
Determine the values of a, b and k. (3 marks) - Three camps, P, Q and R shared 875 bags of beans donated by a charitable organization such that the ratio of P to Q was 2: 3 and that of R to Q was 5: 4. Find the number of bags of beans received by camp Q. (3 marks)
- Find the number of revolutions made by cylindrical roller of diameter 1.02 m and thickness 1.3 m if it rolls over a surface area of 291.72 m2. Use π = 22/7 (3 marks)
- Dr. June needs to import a car from Japan that costs US dollars (USD) 5 000 outside Kenya. He intends to buy the car through an agent who deals in Japanese Yen (JPY). The agent charges a 20% commission on the price of the car and a further 80 325 JPY for shipping the car to Kenya. Find the amount in Kenya shillings that Dr. June will need to send to the agent to get the car given that: (3 marks)
1 USD = Ksh 120
1 USD = 135 JPY - The figure below shows a vertical mast AB. The angles of elevation of the top of the mast from two points C and D on the level ground are 400 and 320 respectively. The distance CD is 50 metres.
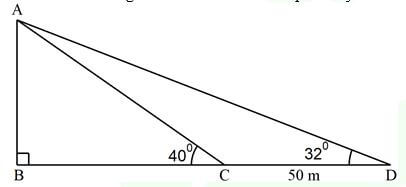
Calculate the distance BC, of the tower correct to 1 decimal place (3 marks) - The figure below shows a solid with the given dimensions.
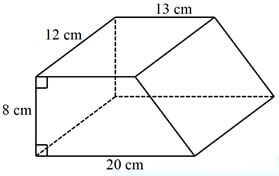
Calculate the mass of the solid to in kilograms given that its density is 3.5 g/cm3. (3 marks) - Solve for x in the equation (3 marks)
9x+1+32x=810 - A lampshade is in the shape of a frustum of a cone such that its slanting height is 30 cm while the top and bottom radii of the lampshade are 10 cm and 17.5 cm respectively. Calculate the surface area of the material used to make the lampshade. (4 marks)
-
- Find the range of values of x which satisfies the following inequalities simultaneously (2 marks)
4x-9≤x+6
4+x≥8-3x - Represent the range of values of x in (a) above on a number line. (1 mark)
- Find the range of values of x which satisfies the following inequalities simultaneously (2 marks)
- The graph below is a histogram showing the marks scored by students in a Mathematics contest.
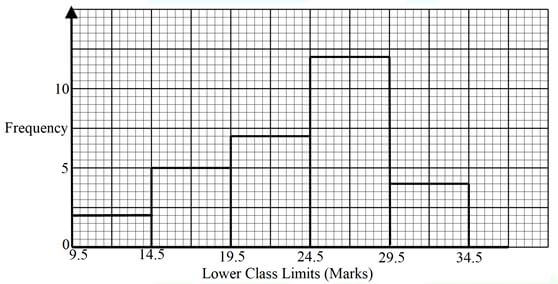
Prepare a frequency distribution table for the above data, hence determine the total number of students who did the contest. (3 marks) - Use logarithms only to evaluate (4 marks)
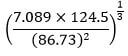
- A sales lady earns a basic salary of Ksh 12 400 per month. In addition, she gets a 2% commission on the first Ksh 80 000 worth of good and a further 3% commission on goods worth over Ksh 80 000. In a certain month, she earned a total of Ksh 20 000. Calculate the value of the goods sold that month. (3 marks)
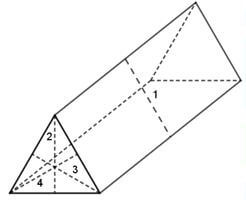
- The figure below shows a triangular prism whose cross-section is an equilateral triangle
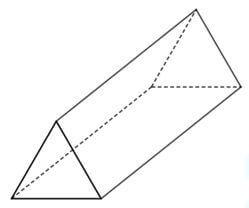
- On the prism, show the positions of the lines of symmetry. (1 mark)
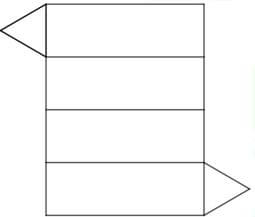
- Draw the net of the prism. (1 mark)
SECTION II (50 Marks)
Answer any five questions in this section
- A straight line L1 has a gradient -1/2 and passes through the point P(-1,3). Another line L2 passes through the points Q(1,-3) and R(4,5)
Find:-
- The equation of L1 in the form y=mx+c, where m and c are constants (2 marks)
- Hence find k given that S(0,k) (1 mark)
-
- The gradient of L2 (1 mark)
- The equation of L2 in the form ax+by=c, where a,b and c are integral values. (2 marks)
- The equation of a line L3 passing through a point T(0,5) and perpendicular to L2. (3 marks)
- Calculate the acute angle that L3 makes with the x-axis. (1 mark)
-
- Water flows through a cylindrical pipe of diameter 7 cm at a rate of 15 m per minute.
- Calculate the capacity of water delivered by the pipe in one minute in litres. Use π=22/7. (3 marks)
- A storage tank that has a circular base and depth 12 m is filled with water from this pipe and at the same rate of flow. Water begins flowing into the empty storage tank at 6.30 a.m. and is full at 1310 hours. Calculate the area of the cross-section of this tank in square metres. (4 marks)
- A school consumes the capacity of this tank in one month. The cost of water is Ksh. 100 for every 1 000 litres and a standing charge of Ksh 1 950. Calculate the cost of the school’s water bill for one month. (3 marks)
-
- Find A-1 given that
 (1 mark)
(1 mark) - An ICT firm bought 8 printers and 12 copiers for a total of Ksh 294 000. Had the firm bought 1 more printer and 3 more copiers, it would have spent Ksh 43 500 more.
- Form two equations to represent the information above. (2 marks)
- Hence, using A-1 in (a) above, calculate the cost of each item. (4 marks)
- A two-digit number is such the that difference between tens and ones digit is 1. If the digits are reversed, the sum of the two numbers is 165. Find the original number (3 marks)
- Find A-1 given that
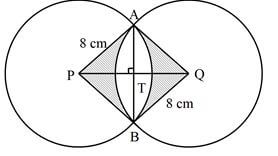
- Two equal circles with centres P and Q and radius 8 cm intersect at points A and B as shown below.

Given that the distance between their centres is 12 cm, find, correct to 4 significant figures;- The length of chord AB (2 marks)
- The area of the shaded region . Use π = 3.142 (8 marks)
- In the figure below, P, Q, R, S and T lie on the circumference of a circle centre O. Line UPV is a tangent to the circle at P. Chord ST of the circle is produced to intersect with the tangent at U. Angles UPT, RST and ORQ are 28º, 100º and 50º respectively.

- Determine the sizes of the following angles;
- RTP (3 marks)
- QTP (3 marks)
- Given that PQ = 6 cm, calculate correct to 1 decimal place, the radius of the circle. (4 marks)
- Determine the sizes of the following angles;
-
- Two trains, A and B are such that they are 40 m long and 160 m long respectively. Their speeds are 60 km/hr and 40 km/hr respectively. The two trains are 100 m apart and moving towards the same direction in a pair of parallel tracks. Calculate the time in seconds it takes train B to completely overtake train A. (4 marks)
- The figure below (not drawn to scale) shows a velocity time graph for a robot in a robotic challenge.

- If the distance covered by the robot in the first 15 seconds was 180 metres, calculate the value of m (3 marks)
- Describe the movement of the robot between the 15th and 45th seconds. (1 mark)
- Calculate the deceleration of the particle in the last 20 seconds. (2 mark)
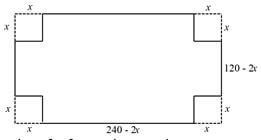
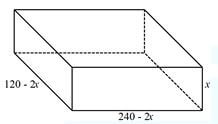
- A farmer wanted to make a trough for cows to drink water. He had a metal sheet of dimensions 240 cm by 120 cm and 1 cm thick. The density of the metal sheet is 2.5 g/cm3. A square of sides x cm is removed from each corner of the rectangle and the remaining part folded to form an open cuboid.
- Sketch the sheet after removing the squares from the four corners, showing all the dimensions. (2 marks)
- Calculate
- the value of x, to the nearest whole number, that maximizes the volume of the cuboid (5 marks)
- hence calculate the maximum volume of the box . (3 marks)
-
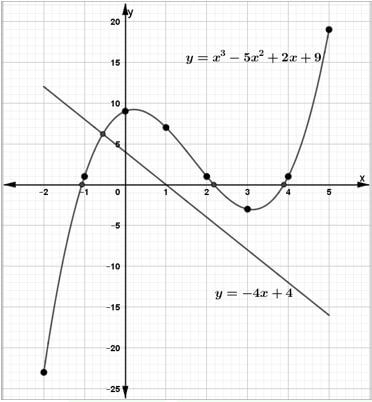
- Complete the table below for the curve y=x3-5x2+2x+9 for -2≤x≤5. (2 marks)
x -2 -1 0 1 2 3 4 5 y 9 - On the grid provided, draw the graph of y=x3-5x2+2x+9 for -2≤x≤5. (3 marks)

- Use the graph in (b) above to find the roots to the following equations:
- x3-5x2+2x+9=0 (2 marks)
- x3-5x2+6x=-5 (3 marks)
- Complete the table below for the curve y=x3-5x2+2x+9 for -2≤x≤5. (2 marks)
MARKING SCHEME
|
NO. |
WORKING |
REMARKS |
||||||||||||||||||
|
1. |
|
Removal of decimal places Expressing as product of prime factors |
||||||||||||||||||
|
|
Total |
|
||||||||||||||||||
|
2. |
2.34 = 2.343434343....... = r Also 1.91 = 1.919191 .. q Hence 232 - 190 |
Expressing 2.34 as a fraction Expressing 1.91 as a fraction Difference between the 2 fractions |
||||||||||||||||||
|
|
Total |
|
||||||||||||||||||
|
3. |
HCF -> 7920 = 24 x 32 x 5 x 11 Other number -> 22 x 32 x 5 = 180 |
Expressing HCF, GCD and the 2 given numbers in power form |
||||||||||||||||||
|
|
Total |
|
||||||||||||||||||
|
4. |
From the graph, x = -3 -> x + 3 = 0 and x = 2 -> x - 2 = 0 |
Factorization by grouping |
||||||||||||||||||
|
|
Total |
|
||||||||||||||||||
| 5. | P:Q = 2:3 ... x 4 = 8:12 R : Q = 5: 4 ... x 3 = 15:12 Hence P:Q:R = 8:12:15 Q --> 12 x 875 8 + 12 + 15 Q --> 12 x 875 = 300 bags 35 |
|||||||||||||||||||
| Total | 3 | |||||||||||||||||||
| 6. | curved surface area of cylinder C.S.A = 22/7 x 1.02 x 1.3 Number of revolutions = 291.72 22/7 x 1.02 x 1.3 = 70 |
|||||||||||||||||||
| Total | 3 | |||||||||||||||||||
| 7. | cost --> 120/100 x 5000 = USD 6000 Shipping --> 80325 = JPY USD 135 Total --> 6000 + 595 = 6595 TOTAL COST --. 6595 X 120 = Ksh 791, 400 |
Total cost in USD Conversion of USD to Ksh |
||||||||||||||||||
| Total | 3 | |||||||||||||||||||
| 8. |
Let BC = x |
Expressing AB in terms of Equating AB to AB 145.9 seen |
||||||||||||||||||
| Total | 3 | |||||||||||||||||||
| 9. | v = {1/2 x 8(13 + 20)} x 12 V = 1584 mass = 3.5 x 1584 1000 = 5.544 kg |
|||||||||||||||||||
| Total | 3 | |||||||||||||||||||
| 10. | 32x + 2 + 32x = 810 32 x 32x + 32x = 810 9(32x) + 32x = 810 10(32x) = 810 --> 32x = 81 32x = 34 2x = 4 --> x = 2 |
Expressing right hand side in terms of base 3 | ||||||||||||||||||
| Total | 3 | |||||||||||||||||||
| 11. | Let the slant length of the smaller cone be L L = 10 L + 30 17.5 17.5L = 10L + 300 L = 300/7.5 = 40 C.S.A = 3.142{(17.5 x 70) - (10 x 40)} C.S.A = 2 592.15 cm2 |
|||||||||||||||||||
| Total | 4 | |||||||||||||||||||
| 12. | 4x - x ≤ 6 + 9 3x ≤ 15 -> x ≤ 5 x + 3x ≥ 8 - 4 4x ≥ 4 -> x ≥ 1 1 ≤ x ≤ 5 |
For x ≤ 5 and x ≥ 1 Compound inequality shown Number line drawn |
||||||||||||||||||
| Total | 3 | |||||||||||||||||||
| 13. |
Frequency distribution table
∑f = 2 + 5 + 7 + 12 + 4 = 30 |
All classes/class boundaries
All frequencies
Total frequency30 seen |
||||||||||||||||||
| Total | 3 | |||||||||||||||||||
| 14. |
Logarithms
|
All logs Correct +/- of logs Correct multiplication by 2 and division by 3 Accuracy |
||||||||||||||||||
| Total | 4 | |||||||||||||||||||
| 15. | Commission -> 20000 - 12400 = 7600 2/100 x 80 000 = 1600 7600 - 1600 = 6000 6 000 = 3/100 x A A = 6 000 x 100/3 = 200 000 Total value 200 000 + 80 000 = 280 000 |
Amount from commission Expression for excess of 80 000 |
||||||||||||||||||
| Total | 3 | |||||||||||||||||||
| 16. |
a) Lines of symmetry
b) Net
|
For all the 4 lines of symmetry drawn
Correct net drawn
Correct measurements transferred from the solid |
||||||||||||||||||
| Total | 2 | |||||||||||||||||||
| 17. |
|
Substituting (-1,3) in y=mx+c y=-1/2 x+5/2 seen 2.5 or equivalent seen 8/3 seen |
||||||||||||||||||
| Total | 10 | |||||||||||||||||||
| 18. |
|
Time difference
Capacity in 400 minutes
Expression for base area |
||||||||||||||||||
| Total | 10 | |||||||||||||||||||
| 19. |
|
Accept if all elements as fractions
Matrix equation
Premultiplying by A^(-1)
Both values
Forming 2 equations in a and b Solution for a and b using any method |
||||||||||||||||||
| Total | 10 | |||||||||||||||||||
| 20. |
|
Angle APT
Area of sector, area of ΔAPB
Area of both segments Shaded Area |
||||||||||||||||||
| Total | 10 | |||||||||||||||||||
| 21. |
|
∠RQT ∠RQP ∠RTP ∠ROQ ∠RTQ ∠QTP Sine Rule applied Half of QT Attempt to get radius |
||||||||||||||||||
| Total | 10 | |||||||||||||||||||
| 22. |
|
Total length
Equation distance to area of trapezium Collecting like terms |
||||||||||||||||||
| Total | 10 | |||||||||||||||||||
| 23. |
|
Correct sketch
Dimensions shown on the sketch
Expression for volume
Equating volume to 0 at maximum volume
Both values of x
Value of x
Internal and external dimensions |
||||||||||||||||||
| Total | 10 | |||||||||||||||||||
| 24. |
|
All the y values (B1 for at least 5 y values )
Linear scales used on both axes – accommodates all table values
All points plotted within the graph paper
Smooth curve drawn
y=0 shown or implied in the roots
All the values of x
attempt to get y=-4x+4 Line y=-4x+4 drawn value of x |
||||||||||||||||||
| Total | 10 |
Download Mathematics Paper 1 Questions and Answers - KCSE 2022 Mock Exams Set 1.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students