Instructions to candidates
- Write your name and index number in the spaces provided above.
- Sign and write the date of examination in the spaces provided above.
- This paper consists of TWO sections: Section I and Section II.
- Answer ALL the questions in Section I and only five questions from Section II.
- Show all the steps in your calculations, giving your answers at each stage in the spaces provided below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.
- Candidates should check the question paper to ascertain that all the pages are printed as indicated and that no questions are missing.
- Candidates should answer the questions in English.
For examiner’s use only
Section I
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Total |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Section II
17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | Total |
|
|
|
|
|
|
|
|
|
QUESTIONS
- Without using a calculator evaluate (3 marks)
-
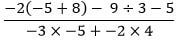
- use mathematical tables to find the:
- The square of 86.46 (1 mark)
- The reciprocal of 27.56 (1 mark)
- Hence or otherwise calculate the value of; (2 marks)
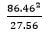
- use mathematical tables to find the:
- The image of a point K (1,2) after translation is K1 (-1,2). What is the coordinate of the point R whose image is R1 (-3,3) after undergoing the same translation? (3 marks)
- A triangle ABC is such that AB = 12cm, and AC = 17cm. if its area is 512cm2, find the size of angle BAC (3 marks)
-
- Find the greatest common divisor of the terms 9x3 y2 and 4xy4 (1 mark)
- Hence factorize completely the expression (2 marks) 9x3 y2-4xy4
- Solve the following inequality and state the integral solutions. (3 marks)
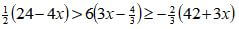
- Find the value of x if. (3 marks)
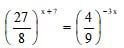
- Security light poles have been erected along both sides of a street in Bahati town. The poles are 50m apart along the left-hand side of the road while they are 80m apart along the right-hand side. At one end of the road the poles are directly opposite each other. How many poles will be erected by time the poles are directly opposite each other at end of the road? (3 marks)
- Using trapezoid rule, estimate the area under the curve y=1/2 x2-2 bounded by lines, x =2 and x=8 and x –axis use six strips. (3marks)
- The marked price of a car in a dealer’s shop was Ksh.450 000. Kawira bought the car at 7% discount. The dealer still made a profit of 13%. Calculate the amount of money the dealer had paid for the car to the nearest shillings. (3marks)
- Kassim has a money box containing 100 mixed shs 5 and shs 10 coins with a total value of shs 600. How many of each type of coin does the box contain. (3 marks)
- A boy walk directly from point Q towards the foot of a vertical flag post 200m away. After covering a distance of 140m, he observes the angle of elevation of the top of the flag post as 75°. Calculate the angle of depression of point Q from the top of the flag post. (3 marks)
- A liquid spray of mass 384g is packed in a cylindrical container of internal radius 3.2cm. Given that the density of the liquid is 0.6g/cm3, calculate to 2dp the height of the liquid in the container. (3 marks)
- The table below shows height of 50 students
Height (cm) Frequency 140 - 144 3 145 - 149 16 150 - 154 20 155 - 159 10 160 - 164 1 - State the modal class (1 mark)
- Calculate the median height. (3 marks)
- Each exterior angle of a regular polygon is a fifth of the interior angle.
- Find the size of the exterior angle (2 marks)
- Find the number of sides of the polygon (1 mark)
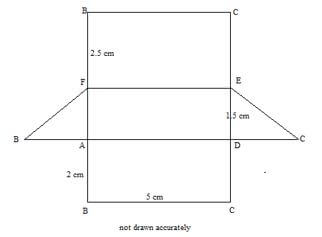
- The diagram below represents a prism whose Cross-section is a right-angled triangle. Draw the net of the solid. (3 marks)
SECTION II
- A straight line y= 2/3 x- 2/3 meets the x – axis at point T.
- Determine the coordinates of T. (2 marks)
- A second line L2 is perpendicular to line L1 at T. Find the equation of line L2 in the form ax+by=c where a, b and c are constants. (3 marks)
- A third line L3 passes through (-4,1) and is parallel to L1. Find; The equation of line L3 in the form y=mx+ c (2 marks)
- The coordinates of point S at which L3 intersects L2. (3 marks)
- Nakuru county government is to construct a floor of an open wholesale market whose area is 800m2. The floor is to be covered with a slab of uniform thickness of 200mm. In order to make the slab, sand, cement and ballast are to be mixed such that their masses are in the ratio 3:2:3 respectively. The mass of dry mass of dry slab of volume 1m3 is 200kg.
- Calculate
- The volume of the slab. (2 marks)
- The mass of the dry slab. (2 marks)
- The mass of cement to be used. (2 marks)
- If one bag of cement is 50kg, find the number of bags to be purchased. (1 mark)
- If a lorry carries 10 tonnes of ballast, calculate the number of lories of ballast to be purchased. (3 marks)
- Calculate
- The vertices of a triangle ABC are A (2,5) B (4,3) and C (2,3). It rotates half-turn about the origin.
- Draw triangle ABC and A1B1C1 under it. (4 marks)
- The image A’B’C is mapped onto A’’B’’C’’ under a reflection R in the line x=0 followed by a translation
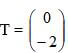. Find the coordinates of A’’B’’ and C’’ and A’’’B’’’C’’’. Hence draw triangle A’’’B’’’C’’’. (4 marks) - Find the area of the triangle A’’B’’C’’. (2 marks)
- A trader bought 2 cows and 9 goats for a total of Ksh. 98,200. If she had bought 3 cows and 4 goats, she would have spent Ksh. 2, 200 less.
- Form two equations to represents the above information. (2marks)
- Use the matrix method to determine the cost of a cow and that of a goat. (4marks)
- The trader later sold the animals she had bought making a profit of 30% per cow and 40% per goats. Calculate the total amount of money she received. (2marks)
- Determine corrects to 4 significant figures the percentage profit the trader made from the sale of animals. (2marks)
- In the figure below OAB is a triangle in which M divides OA in the ratio 2:3 and N divides OB in the ratio 4:1. AN and BM intersects at X.
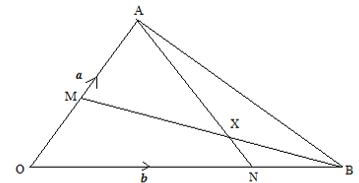
Given that OA = a andOB=b express in terms of a and b.- AN (1 mark)
- BM (1mark)
- AB (1mark)
- If AX= sAN and BX = tBMwheres and t are constants. Write two expressing for OX in terms of a, b, s and t. (2marks)
- Find the value of s and t, and hence express OX in terms of a and b. (5marks)
- Town B is 20km N600W from village A. Town B is 25km 0400 from town C. Village D is due East of town C and dues South of village A
- Using a scale 1:500,000 draw a diagram showing a relative position of town B, town C, village A and village D (4 marks)
- Determine;
- Distance between village A and town C (1 mark)
- Distance between town C and village D (1 mark)
- Compass bearing of town C from village A (1 mark)
- Compass bearing of village D from town B (1 mark)
- Determine the area enclosed by the diagram in (a) above in hectares (2 marks)
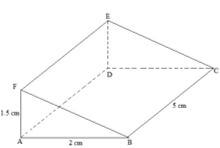
- The figure below shows a frustrum made from a right pyramid, such that AB=DC=16cm, BC=AD=10cm, FG=EH=18cm, GH=FE=7.5cm, CH=BG=AF=DE=15cm. If the altitude of the frustrum is 14.6cm, find:
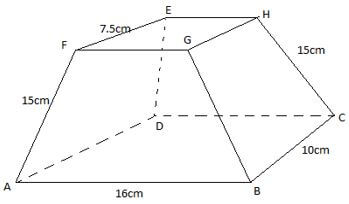
- The altitude of the pyramid made from the frustrum. (2 marks)
- The surface area of the frustrum. (5 marks)
- The volume of the frustrum. (3 marks)
- The distance S meters from a fixed point O, covered by a particle after t seconds B given by the equation S = t3 – 6t2 + 9t + 5
- Calculate the gradient of the curve at t = 0.5 seconds (3 marks)
- Determine the values of S at the turning points of the curve (3 marks)
- Sketch the curve in the space provided. (4 marks)
. Find the coordinates of A’’B’’ and C’’ and A’’’B’’’C’’’. Hence draw triangle A’’’B’’’C’’’. (4 marks)
MARKING SCHEME
- Without using a calculator evaluate (3 marks)
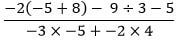
Numerator
-2 (-5 + 8) - 9 ÷ 3 - 5
-6 - 9 ÷3 +5
-6 - 3 - 5 = -14
Denominator
-3 x -5 + -2 x 4
15 - 8 = 7
Quotient
-14/7 = -2 -
- use mathematical tables to find the:
- The square of 86.46 (1 mark)
86.462=7475 - The reciprocal of 27.56 (1 mark)
1/27.56 = 1/2.756 x 102 = 0.03628
86.462 = 7475 x 0.03628
27.56
= 271.2
- The square of 86.46 (1 mark)
- Hence or otherwise calculate the value of; (2 marks)
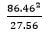
- use mathematical tables to find the:
- The image of a point K (1,2) after translation is K1 (-1,2). What is the coordinate of the point R whose image is R1 (-3,3) after undergoing the same translation? (3 marks)
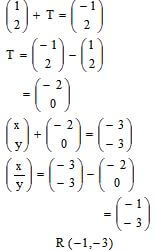
- A triangle ABC is such that AB = 12cm, and AC = 17cm. if its area is 512cm2, find the size of angle BAC (3 marks)
Area = 1/2 ab sin θ
51 = 1/2 x 12 x 17 sin θ
51 = 6 x 17 sin θ
6 x 1 6 x 1
sin θ = 0.5
θ = 30º -
- Find the greatest common divisor of the terms 9x3 y2 and 4xy4 (1 mark)
GCD is xy2
xy2(9x2 - 4y2)
xy2(3x - 2y)(3x + 2y) - Hence factorize completely the expression (2 marks) 9x3 y2-4xy4
- Find the greatest common divisor of the terms 9x3 y2 and 4xy4 (1 mark)
- Solve the following inequality and state the integral solutions. (3 marks)
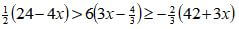
12 - 2x > 18x - 8
= 20x > -20
x < 1
18x - 8 ≥ -28 - 2x
20x ≥ -20
x ≥ -1
-1 ≤ x < 1 - Find the value of x if. (3 marks)
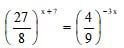
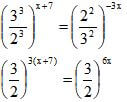
3(x + 7) = 6x
3x + 21 = 6x
3x = 21
x = 7 - Security light poles have been erected along both sides of a street in Bahati town. The poles are 50m apart along the left-hand side of the road while they are 80m apart along the right-hand side. At one end of the road the poles are directly opposite each other. How many poles will be erected by time the poles are directly opposite each other at end of the road? (3 marks)
LCM of 50 and 80
= 400
Number of poles = 400 + 400
50 8
= 13 - Using trapezoid rule, estimate the area under the curve y=1/2 x2-2 bounded by lines, x =2 and x=8 and x –axis use six strips. (3marks)
Coordinates: 0,2.5,6.0,10.5,16.0,22.5,30
A= ½ x1 (6+30) +2(2.5+6.0+10.5+16.0+22.5)
= 72.5 - The marked price of a car in a dealer’s shop was Ksh.450 000. Kawira bought the car at 7% discount. The dealer still made a profit of 13%. Calculate the amount of money the dealer had paid for the car to the nearest shillings. (3marks)
93 x 450 000
100
418 500
418500 x 100
113
370,353.98
= 370, 354 - Kassim has a money box containing 100 mixed shs 5 and shs 10 coins with a total value of shs 600. How many of each type of coin does the box contain. (3 marks)
x +y = 100
5x + 10y = 600
5x + 5y = 500
5x + 10y = 600
-5y = -100
y = 20
x = 80
20 sh 10 coins
80 shs 5 coins - A boy walk directly from point Q towards the foot of a vertical flag post 200m away. After covering a distance of 140m, he observes the angle of elevation of the top of the flag post as 75°. Calculate the angle of depression of point Q from the top of the flag post. (3 marks)
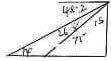
tan 75 = h/60
h = 60 tan 75 = 223.42
tan x = 223.92/200
x = 48.2
Angle of depression = 48.2 - A liquid spray of mass 384g is packed in a cylindrical container of internal radius 3.2cm. Given that the density of the liquid is 0.6g/cm3, calculate to 2dp the height of the liquid in the container. (3 marks)
D = m/v
0.6 = 384/0.6 => 22/7 x 3.2 x 3.2 x h
640 = 32.18h
h = 19.89 - The table below shows height of 50 students
Height (cm) Frequency 140 - 144 3 145 - 149 16 150 - 154 20 155 - 159 10 160 - 164 1 - State the modal class (1 mark)
M = L + n/2 - c x i
f
= 149.5 + 25 - 19 x 5
20
= 151 - Calculate the median height. (3 marks)
- State the modal class (1 mark)
- Each exterior angle of a regular polygon is a fifth of the interior angle.
- Find the size of the exterior angle (2 marks)
x + 1/5x = 180
x = 150
180 - 150 = 30 - Find the number of sides of the polygon (1 mark)
360/30 = 12 sides
- Find the size of the exterior angle (2 marks)
- The diagram below represents a prism whose Cross-section is a right-angled triangle. Draw the net of the solid. (3 marks)
SECTION II
- A straight line y= 2/3 x- 2/3 meets the x – axis at point T.
- Determine the coordinates of T. (2 marks)
At the x-axis, y = 0
0 = 2/3x - 2/3
2/3x = 2/3
x = 1
T(1,0) - A second line L2 is perpendicular to line L1 at T. Find the equation of line L2 in the form ax+by=c where a, b and c are constants. (3 marks)
y = 2/3x - 2/3
m1 = 2/3 m2 = -3/2
y - 0 = -3
x - 1 2
2y = -3x + 3 - A third line L3 passes through (-4,1) and is parallel to L1. Find; The equation of line L3 in the form y=mx+ c (2 marks)
i) . m1 = m3 = 2/3point(-4,1)
y - 1 = 2
x + 4 3
y - 1 = 2/3x + 8/3
y = 2/3x + 11/3
ii). y = 2/3x + 11/3
(2y + 3x = 3)3
(3y - 2x = 11) 2
6y + 9x = 9
6y - 4x = 22
13x = -13
x = -1
y = 3
S(-1, 3) - The coordinates of point S at which L3 intersects L2. (3 marks)
- Determine the coordinates of T. (2 marks)
- Nakuru county government is to construct a floor of an open wholesale market whose area is 800m2. The floor is to be covered with a slab of uniform thickness of 200mm. In order to make the slab, sand, cement and ballast are to be mixed such that their masses are in the ratio 3:2:3 respectively. The mass of dry mass of dry slab of volume 1m3 is 200kg.
- Calculate
- The volume of the slab. (2 marks)
800 x 0.2
= 160cm3 - The mass of the dry slab. (2 marks)
160 x 2000
= 320, 000 - The mass of cement to be used. (2 marks)
cement = 2/8 x 32000
= 80,000
- The volume of the slab. (2 marks)
- If one bag of cement is 50kg, find the number of bags to be purchased. (1 mark)
Bags = 80000
50
= 1600 - If a lorry carries 10 tonnes of ballast, calculate the number of lories of ballast to be purchased. (3 marks)
Ballast = 3/8 x 320000
= 120 000 tonnes
= 120 lorries
- Calculate
- The vertices of a triangle ABC are A (2,5) B (4,3) and C (2,3). It rotates half-turn about the origin.
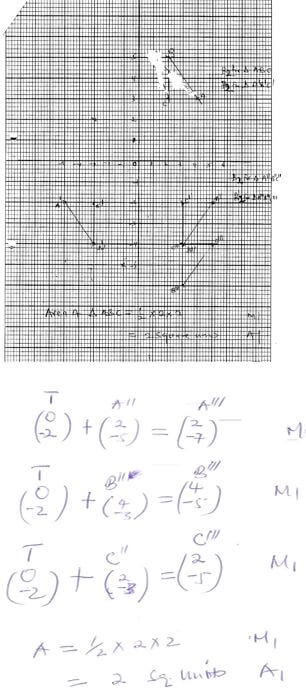
- Draw triangle ABC and A1B1C1 under it. (4 marks)
- The image A’B’C is mapped onto A’’B’’C’’ under a reflection R in the line x=0 followed by a translation 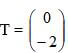. Find the coordinates of A’’B’’ and C’’ and A’’’B’’’C’’’. Hence draw triangle A’’’B’’’C’’’. (4 marks)
- Find the area of the triangle A’’B’’C’’. (2 marks)
- A trader bought 2 cows and 9 goats for a total of Ksh. 98,200. If she had bought 3 cows and 4 goats, she would have spent Ksh. 2, 200 less.
- Form two equations to represents the above information. (2marks)
2c +9g = 98200
3c + 4g= 96000 - Use the matrix method to determine the cost of a cow and that of a goat. (4marks)
(2 9)c = (98200)
3 4 9 96000
2 9 =1 ( 4 -9)
3 4 19 -3 2
-1 (4 -9) (2 9) (c)=-1 (4 -9)(98200)
19 -3 2 3 4 19 -3 2 96000
(c = -1 (-471200)
G 19 -102600)
(c=(24800)
G 54000)Cows = Ksh 24800
Goats = Ksh. 5400 - The trader later sold the animals she had bought making a profit of 30% per cow and 40% per goats. Calculate the total amount of money she received. (2marks)
Cows = Ksh 24800
Goats = Ksh. 5400
Selling price = 2 x 24800 x 1.3 + 9 x 5400 x 1.4
= 132 520 - Determine corrects to 4 significant figures the percentage profit the trader made from the sale of animals. (2marks)
132520 – 98200 x 100%
98200
34.95%
- Form two equations to represents the above information. (2marks)
- In the figure below OAB is a triangle in which M divides OA in the ratio 2:3 and N divides OB in the ratio 4:1. AN and BM intersects at X.
Given that OA = a andOB=b express in terms of a and b.- AN (1 mark) AN= 2/3B – A
- BM (1mark) BM= 2/5 a – b
- AB (1mark) AB = B-A
- If AX= sAN and BX = tBMwheres and t are constants. Write two expressing for OX in terms of a, b, s and t. (2marks)
- Find the value of s and t, and hence express OX in terms of a and b. (5marks)
OX = OB+BX
= B+K (2A-B)
= 2/5 KA +(i-k) b
OX = OA + AX
= (i-h)a+2/3 hb
2/5 ka +(1-k)b)= (1-h)a +2/3 b
2/5k=1-h……..(i)
1-k=2/3h……..(2)
From (1)h=1-2/5k
1-k=2/3(1-2/5k)
K=5/11
h= 1- 2/11
= 9/11
OX=2/5 X 5/11a+b (1-5/11)
=2/11a+6/11b
- Town B is 20km N600W from village A. Town B is 25km 0400 from town C. Village D is due East of town C and dues South of village A
- Using a scale 1:500,000 draw a diagram showing a relative position of town B, town C, village A and village D (4 marks)
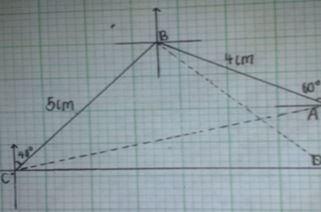
- Determine;
- Distance between village A and town C (1 mark) 35 km
- Distance between town C and village D (1 mark) 33.5 km
- Compass bearing of town C from village A (1 mark) S75ºW
- Compass bearing of village D from town B (1 mark) S42ºE
- Determine the area enclosed by the diagram in (a) above in hectares (2 marks)
Area of ADC=1/2×6.7cm×1.8cm=6.03cm2
Area of ABC =s=1/2 (7+4+5)=8
√(8(8-7)(8-4)(8-5))= √96
9.7980 cm2
Total area 6.03 cm2+9.7980 cm2=15.828 cm2
Area of the scale 1cm2= 25km2
15.828cm2×25km2=395.7 km2
395.7 km2×100=39570hectares
- Using a scale 1:500,000 draw a diagram showing a relative position of town B, town C, village A and village D (4 marks)
- The figure below shows a frustrum made from a right pyramid, such that AB=DC=16cm, BC=AD=10cm, FG=EH=18cm, GH=FE=7.5cm, CH=BG=AF=DE=15cm. If the altitude of the frustrum is 14.6cm, find:
- The altitude of the pyramid made from the frustrum. (2 marks)
L.S.F= =
24x=18x+262.8
6x=262.8
X=43.8
Hence H=43.8+14.6
=58.4cm - The surface area of the frustrum. (5 marks)
18x7.5=135
24x10=240
0.5x2x14.69693846x42=617.2714
0.5x2x14.94782593x17.5=261.5869538
ATOTAL=135+240+617.27+261.59
=1,253.858354cm2 - The volume of the frustrum. (3 marks)
V=VB.P-VS.P
=( X 240 X 58.4)+( X 135X 43.93)
=4672-1976.85
=2695.15 cm3
- The altitude of the pyramid made from the frustrum. (2 marks)
- The distance S meters from a fixed point O, covered by a particle after t seconds B given by the equation S = t3 – 6t2 + 9t + 5
- Calculate the gradient of the curve at t = 0.5 seconds (3 marks)
At t =0.5seconds.
Gradient =
=3.75mwhen
(t-1) (t-3) = 0t= 1 or 3 seconds
when t=1b, S=1-6+9+5
=9m
When t = 3s, S=
=5m.
At t = 1b,max turning point
At t =
At (3,5) Min. turning point. - Determine the values of S at the turning points of the curve (3 marks)
- Sketch the curve in the space provided. (4 marks)
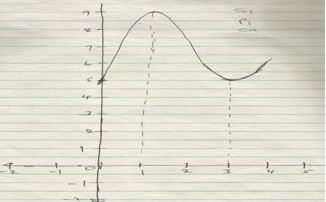
- Calculate the gradient of the curve at t = 0.5 seconds (3 marks)
Download Mathematics Paper 1 Questions and Answers - Sunrise 2 Evaluation Mock Exams 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students
Join our whatsapp group for latest updates