Mathematics Paper 1 Questions and Answers - Achievers Joint Mock Exams 2023

Next Topic »
Mathematics Paper 2 Questions and Answers - Achievers Joint Mock Exams 2023

Download PDF for future reference Get on Whatsapp for 50/-

Instructions to candidates

This paper consists of two sections I, II.
Answer all the questions in section 1 and any five questions from section II.
Show all steps in your calculations, giving answers at each stage in the spaces provided below each question.
Marks may be given for correct working even if the answer is wrong.
Non-programmable silent electronic calculators and KNEC mathematical tables may be used.

For Examiner’s Use Only.
SECTION I

Questions	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	Total
marks

SECTION II

Questions	17	18	19	20	21	22	23	24	Total
Marks

QUESTIONS

Evaluate 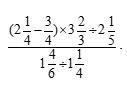$maths 1 1$ (3mks)
Use square roots, reciprocal and square tables to evaluate to 4 significant figures the expression 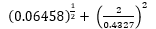$2 adad$ (4mks)
Three similar 21-inch television sets and five similar 17-inch television cost Ksh.129, 250. The difference between the cost of two 21-inch television sets and four 17-inch television sets is Ksh. 22,000. Calculate the price of a 21-inch television set and that of 17-inch television set. (3mks)
Three numbers, 1400, 1960 and n, have a G.C.D and L.C.M of 70 and 2² x 5² x 7² x 1¹ respectively. Find the least possible value of n (3mks)
Find the equation of a straight line which is equidistant from the points A (2,3) and B (6,1) (3mks)
Solve for x in the equation. (3mks)
9^(2x-1) x 3^(2x+1) = 243
An open rectangular box measures externally 32cm long, 27cm wide and 15cm deep. The box is made up of metal 1cm thick. If it has a mass of 1.5kg, what is the density of the box to 4 significant figures? (3mks)
Using the three quadratic identities only factorize and simplify: (3mks)
(x-y)²- (x+y)²
(x²+ y²)²- (x²- y² )²
An airplane leaves point A (60⁰S, 10⁰W) and travels due East for a distance of 960 nautical miles to point B. determine the position of B and the time difference between points A and B. (3mks)
A salesman earns 3% commission for selling a chair and 4% commission for selling a table. A chair fetches K£ 75. One time, he sold ten more chairs than tables and earned seven thousand, two hundred Kenya shillings as commission. Find the number of tables and chairs sold. (3mks)
A Kenyan company received US Dollars 200,000. The money was converted into Kenya shillings in a bank which buys and sells foreign currencies as follows:
      Buying Selling
   (in Kenya shillings) (in Kenya shillings)
1 US Dollar 77.24 77.44
Sterling Pound 121.93    122.27
1. Calculate the amount of money, in Kenya shillings, the company received. (1 marks)
2. The company exchanged the Kenya shillings calculated in (a) above, into sterling pounds to buy a car from Britain. Calculate the cost of the car to the nearest sterling pound. (2 marks)
Tap A fills a tank in 6 hours, tap B fills it in 8 hours and tap C empties it in10 hours. Starting with an empty tank and all the three taps are opened at the same time, how long will it take to fill the tank? (3 marks)
The length of a rectangle is increased by 20% while the width is decreased by 10% . Find the percentage change in area. (3 marks)
In the figure below, AC is an arc of a circle centre D. Angle ADC = 600, AD = DC = 7cm and CB = 5cm.

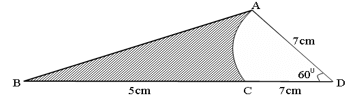
Calculate
1. The area of triangle ADB (2 marks)
2. The area of the shaded region. (2 marks)
Solve 4 ≤ 3x – 2 < 9 + x , hence list the integral values that satisfies the inequality. (3 marks)
A transformation whose matrix is given by (2x-1 - 32x) maps a triangle with area 8 cm2 onto another triangle with area 72 cm2, calculate the value of x (3 marks )

SECTION II

The distance between two towns A and B is 760 km. A minibus left town A at 8:15a.m and traveled towards B at an average speed of 90km/h. A matatu left B at 10:35a.m and on the same day and travelled towards A at an average speed of 110km/h.
1. 1. How far from A did they meet? (4mks)
  2. At what time did they meet? (2mks)
2. A motorist starts from his home at 10:30 a.m on the same day and traveled at an average speed of 100km/h. He arrived at B at the same time as the minibus. Calculate the distance from B to his home. (4mks)
The income tax rates in a certain year are as shown below.

Income (k₤ – p.a

Rate (KSh. per ₤)

1 – 4200

2

4201 – 8000

3

8001 – 12600

5

12601 – 16800

6

16801 and above

7

Omar pays Sh. 4000 as P.A.Y.E per month. He has a monthly house allowance of KSh.10800 and is entitled to a personal relief of KSh. 1,100 per month. Determine:
1. his gross tax per annum in Kshs (2 Marks)
2. his taxable income in K₤ per annum (2 marks)
3. his basic salary in Ksh. per month (2marks)
4. his net salary per month (2 mark
The parents of a certain mixed secondary school decided to buy a school van worth Ksh. 900,000. Each student was to contribute the same amount of money. 50 students were transferred from the school; as a result, each if the remaining students had to pay Ksh. 600 more.
1. Find the original number of the students in the school. (5mks)
2. Find the percentage change in contributions per student. (3mks)
3. If the ratio of boys to girl in the school was 11: 7 find the amount money contributed by boys alone. (2mks)
Using a ruler and a pair of compasses only construct triangle ABC such that angle BAC= 90⁰, AC= 5 cm and BC = 10 cm. (3 marks)
1. Circumscribe a circle on the triangle ABC constructed above (3 marks)
2. Measure the radius of the circle (1 mark)
3. Find the difference in the area of the circumcircle and the triangle. (3 marks)
The coordinates of a triangle ABC are A(1, 1) B(3, 1) and C (1, 3).
1. Plot the triangle ABC. (1 mark)
2. Triangle ABC undergoes a translation vector (2 , 2 ). Obtain the image of A' B' C ' under the transformation, write the coordinates of A' B' C'. (2 marks)
3. A' B' C' undergoes a reflection along the line X = 0, obtain the coordinates and plot on the graph points A" B" C", under the transformation (2 marks)
4. The triangle A" B" C" , undergoes an enlargement scale factor -1, centre origin. Obtain the coordinates of the image A'" B"' C"'. (2 marks)
5. The triangle A"' B"' C"' undergoes a rotation centre (1, -2) angle 1200. Obtain the coordinates of the image Aiv Biv Civ. (2 marks)
6. Which triangles are directly congruent. (1 mark)
The figure below shows triangle OPQ in which OS = ¹/₃ OP and OR = ¹/₃ OQ. T is a point on QS such that QT = ³/₄ QS
1. Given that OP = p and OQ = q, express the following vectors in terms of p and q.
  1. SR (1 Mark)
  2. QS (2 Marks)
  3. PT (2 Marks)
  4. TR (2 Marks)
  5. show that point PTR are collinear. (3mks)

Fill the table below for the function.
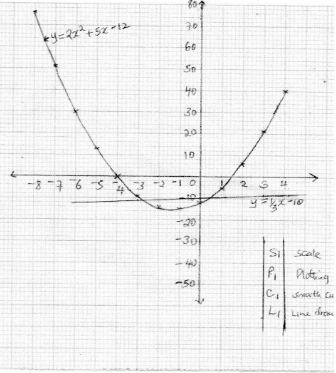
y = 2x² + 5x – 12 for -8 ≤ x ≤ 4 (2 marks)

X	-8	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4
2x²	128					18				2			32
5x	-40					-15				5			20
-12	-12					-12				-12			-12
Y	76					-9				-5			40

Using the table, draw the graph of the function y = 2x2 + 5x – 12. Use the scale 1cm to 1 unit on the x-axis and 1cm for 10 units for the y – axis (4 mark

Use the graph drawn above to solve the following equations.
1. 2x² + 5x – 12 = 0 (2 marks)
2. 3 – 7x – 3x² = 0 (2 marks)

The displacement, S meters of a moving particle after t seconds is given by S=2t³-5t²+4t+3
Determine:
1. The velocity of the particle when t=4 seconds (3marks)
2. The value of t when the particle is momentarily at rest (3 marks)
3. The displacement when the particle is momentarily at rest (2 marks)
4. The acceleration of the particle when t=10 seconds (2 marks)

MARKING SCHEME

N: 2¹/₄ - ³/₄ = 9 - 3 = 6 = 3
4 4 2
³/₂ x ¹¹/₃ ÷ ¹¹/₅ = ³/₂ x ¹¹/₃ x⁵/₁₁ = ⁵/₂

D: ¹⁰/₆ ÷ ⁵/₄ = ¹⁰/₆ x ⁴/₅ = ⁴/₃

^5/₂ / _⁴/3 = ⁵/₂ x ³/₄ = ¹⁵/₈ = 1⁷/₈
(0.06458)1/2 = √6.458 x 10^-2 = 2.5413 x 10^-1
(2/0.4327)² = [2(¹/_4.327 x 10^-1]² = {2(0.2311 x 10)}²
= (2 x 2.311)² = 4

0.25413 + 21.363 = 21.61713
= 21.62
3x + 5y = 129250
2x - 4y = 22000

6x + 10y = 258500
6x - 12y = 66000
22y = 192500
y = 8750

2x - 4(8750) = 22000
2x - 35000 = 22000
2x = 57000
x = 28500
17 inch TV = sh 8750 ; 21 inch tv = sh 28500
gcd = 70 = 2 x 5 x 7
l.c.m = 23 x 52 x 7
1960 = 23 x 5 x 72
oter number = 2 x 5 x 7 x11
= 770
midpoint = (2 + 6 , 3 + 1) = (4, 2)
2 2
m¹ = 1 - 3 = -2 = -1
6 - 2 4 2
m² = 2

y - 2 = 2
x - 4
y - 2 = 2x - 8
y = 2x - 6
32(2x - 1) x 3(2x+1) = 3⁵
34x - 2 + 2x + 1 = 3⁵
36x - 1 = 3⁵
6x - 1 = 5
6x = 6
x = 1
volume of materias ofte box = external - internal volume
= (32 x 27 x 15) - (30 x 25 x 14) = 2460cm³
mass of te box = 1.5 = 1.5 = 1500
density = mass/volume = 1500/2460
=0.6098 g/cm³
= (2x)(-2y) = -4xy = -1
(2x²)(2y²) 4x²y² xy
didstance = ∅ x 60 cos 60
∅ x 60 x 0.5 = 960
∅ = 960/30 = 32 - lonitude difference
B(60ºS, 22ºE)
total difference in time = 32 x 4 min = 128 minutes
= 2 hours 8 minutes
a chair = 30 = 30 x 20 = 600
a table = 75 = 75 x 20 = 1500

no of chairs = x
no of tables = x - 10

3/100 x 600x + 4/100 x 1500(x - 10) = 7200

18x + 60(x - 10) = 7200
18x + 60x - 600

78x = 7800

x = 100 chairs
x - 10 = 90 tables
1. 200000 us dollars
  1 US dollars = s 7724
  
  200000 = 200000 x 77.24 = 15 448 000
  1
2. 1 sterling pound = ks 122.27
  ? = 15448000
  1 x 15448000 = 126343
  122.27
new lengths = 120%L = 1.2L
new month = 90%W = 0.9W

New area = 1.2L x 0.9W = 1.08LW

Original area = LW

% change = 1.08LW - LW x 100
LW
= 8% increase
1. area of a triangle = 1/2 ab sin
  1/2 x 7 x 12 sin 60°
  1/2 x 7 x 12 x 0.866 = 36.372 cm²
2. shaded area = area of triangle - area of sector
  = 36.372 - (60/360 x 22/7 x 7 x 7)
  = 36.372 - 25.667 = 10.705 cm²
4 ≤ 3x - 2 3x - 2 < 9 + x
6 ≤ 3x 2x < 11
2 ≤ x x < 5.5

2 ≤ x < 5.5
integral values 2,3,4,5
ASF = determinant of transformation matrix
72/8 = (2x - 1)x - 2(-3)
9 = 2x² - x + 6
2x² - x - 3 = 0
(2x - 3) (x + 1) = 0
x = 1.5 or x = -1
1. 1. 10.35
    8.15
    2.20 = 2 hours 20 minutes = 2¹/₃ hrs
    distance covered in that time = 2¹/₃ x 90 210 km
    distance remainin = 760 - 210 = 550km
    relative speed = 90 + 110 = 200km/h
    time taken to meet D/R.S = 550/200 = 2.75hr
    distance covered by minibus in 2.75 hr
    = 2.7 x 9 = 247.5k
    
    distance from A = 210 + 247.5 = 457.5 km
    1. 10.35 am + 2 hours 45 min
      
      10:35
      2:45
      13.20
      -12:00
      1.20 pm
2. time taken by minibus from A to B = 760/90 = 8⁴/₉ hrs
  time A arrived at B
  8:15 am + 8:27 min
  8:15
  8:27
  -16:42
  -12:00
  4:42 pm
  
  time taaaken by motorist from ome to B
  1642
  -10:30
  6:12
  
  6¹/₅ hrs
  
  distance covered by motorists from home to B
  
  100 x 6¹/₅ = 100 x 6.2 = 620 km
1. his ross tax p.a in ksh
  (4000 x 12) + (1100 x 12)
  48000 + 13200 = 61200
2. 1 slab = 4200 x 2
  2 slab = 3800 x 3
  3 slab = 4600 x 5
  4 slab = y x 6 = 61200 - 42800
  y = kf 3066.67
  
  taxable income = (12600 + 3066.67) = kf 15 666.67
3. 15666.67 x 20 - 10800 = 15311.12
  1.2
  26111.12 - 10800
4. 26111.12 - 4000 = 22111.12
900000 - 900000 = 600
x - 50 x
1. 900000x - (900000)(x - 50) = 60 (x² - 50x)
  45000000 = 600x² - 30000x
  ans = 300 students
2. 900000/300 = 3000
  600 x 100
  3000
  = 20%
3. total ratio = 18
  11/18 x 900000
  = 550000
1. $20 dfd 1$
2. R - 50 cm
3. (22/7 x 5²) - (1/2 x 5 x 8.6)
  - 78.5714 - 21.5 = 57.0714 cm ²
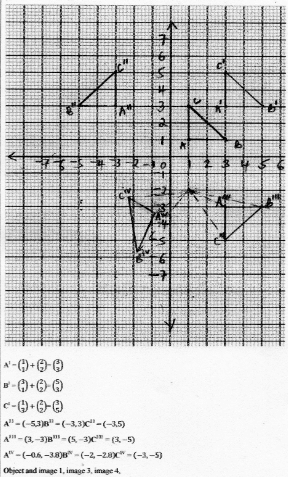
$21 adad 1$
1. $23 ssfs 1$
2. 1. 2x² + 5x - 12 = y
    2x² + 5x - 12 = 0
    0 = y
    x = -4 or 1.5
  2. 2x² + 5x - 12 = y³
    y = 1/3x - 10 x = -2.8 or o.4
1. v = ds/dt
  v = 64² - 104 + 4
  v at 4
  v = 6(4)² - 10(4) + 4
  = 96 - 40 + 4
  = 60 m/s
2. at rest
  6t² - 10t + 4 = 0
  6t² - 6t - 4t + 4 = 0
  6t(t - 1) - 4(t - 1) = 0
  6t = 4
  t = 4/6s = 2/5 (S)
  t = 1s
3. displacement of t = 1
  ans = 2²⁵/₂₇ m
4. a = dv/dt
  = 12t - 10
  a at t = 10
  120 - 10
  = 110 m/s²