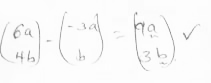Mathematics Paper 1 Questions and Answers - Bunamfan Cluster Pre Mock Exam 2022

Share via Whatsapp

Next Topic »
Mathematics Paper 2 Questions and Answers - Bunamfan Cluster Pre Mock Exam 2022

Download PDF for future reference Get on Whatsapp for 50/-

INSTRUCTIONS TO CANDIDATES

The paper contains TWO sections; section I and section II
Answer all the questions in section I and ANY FIVE questions from section II
Show all the steps in your calculations; giving your answers at each stage in the spaces provided below each question.
Marks may be given for correct working even if the answer is wrong.
Non-programmable silent electronic calculators and KNEC mathematical tables maybe used.

Questions

SECTION I (50 MARKS)
Answer all the questions in this section

Use mathematical tables to evaluate; (3mks)
2 + 4
(3.432)^½ √0.0684
A wholesaler sold a cell phone to a retailer making a profit of 20%. The retailer later sold the cell phone for Ksh.3120 making a profit of 30% calculate the amount of money the wholesaler had paid for the cell phone. (3 mks)
A piece of plot in Gilgil measuring 27m by 16m is to be divided into smaller rectangular units leaving no remainder. Calculate the highest number of smaller units whose dimensions are each greater than 1m that can be obtained from the plot. (3mks)
A Kenyan bank buys and sells foreign currencies as shown below.

Buying Selling

1 US Dollar 76.38 75.19

1 UK Pound 132.92 132.95

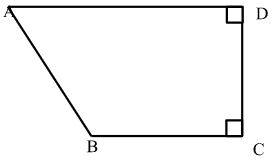
A tourist arrived in Kenya from Britain with 126,000 UK sterling pounds. He converted the pounds into Kenyan shillings. While in Kenya he spent 45 of the money. He changed the balance to US dollars. Calculate to the nearest Dollar, the amount he received. (3 mks)
The figure below shows quadrilateral ABCD in which AB = 6cm. BC = 12CD, CD = DA and angle ADC = angle BCD = 900.

Calculate the area of the quadrilateral ABCD. (4 Mks)
The exterior angle of a regular polygon is (χ - 50)° and the interior angle is (2χ + 20)°. Find the number of sides of the polygon. (3 mks)
simplify: (3 mks)
12x² + ax - 6a²
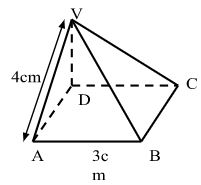
9x² - 4a²
The diagram below represents a right pyramid on a square base of side 3cm. The slant edge of the pyramid is 4cm.
1. Draw a labelled net of the pyramid. (2 Mks)
2. On the net drawn, measure the height of a triangular face from the top of the pyramid. (1 Mk)
The mass of two similar solids are 324g and 768g. Find
1. height of the smaller solid if the height of the bigger solid is 20cm. (2 mks)
2. the surface area of the smaller solid if the surface area of the bigger solid is 40cm². (2 mks)
State all the integral values which satisfy the inequality (3mks)
3a + 2< 2a + 3 < 4a + 15
4 5 6
The length of a rectangle is (3x+1)cm, its width is 3cm shorter than its length. Given that the area of the rectangle is 28cm2, find its length. ` (3marks)
The curved surface area of a cylindrical container is 1980cm2.if the radius of the container is 21cm, calculate to one decimal place the capacity of the container. (take π=227) (4 marks)
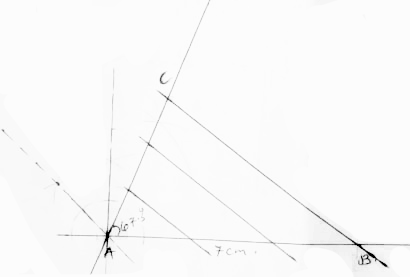
Using a ruler and a pair of compasses only, draw a line AB = 7cm long. Construct < BAC = 67.50. Use line AC to divide AB into 3 equal parts. (2 mks)
Given that Sin (x + 4°) = Cos (3x)°. Find tan (x + 40°) to 4 s.f. (3 mks)
Given that log₁₀7=0.8451 and log₁₀6=0.7782. find log₁₀25.2 (3 mks)
1. The position vector OA = - 3a i + b j, OB = 6a i + 4b j and OC = 15a i + 7b j, where a and b are scalars. Find in column form;
  1. AB (1 mk)
  2. AC (1 mk)
2. Hence show that A,B and C are collinear. (1 mk)

SECTION II (50 MARKS)
Answer any five questions in this section

A straight line passes through the points (8, -2) and (4, -4)
1. Write its equation in the form ax + by + c = 0 where a, b and c are integers. (3 Mks)
2. If the line in (a) above cuts the x-axis at point p, determine the coordinates of P. (2 Mks)
3. Another line which is perpendicular to the line in (a) above passes through point P and cuts the y-axis at the point Q. Determine the coordinates of point Q. ( 3 Mks)
4. Find the length of QP (2 Mks)
A group of people planned to contribute equally towards buying land at a price of Shs 180,000. However 3 members of the group withdrew from the project. As a result, each of the remaining members were to contribute KShs. 3000 more.
1. Find the original number of members in the group. (6 Mks)
2. How much would each person have contributed if the 3 people had not withdrawn.(2 Mks)
3. Calculate the percentage increase in the contribution per person caused by the withdrawal. (2 Mks)
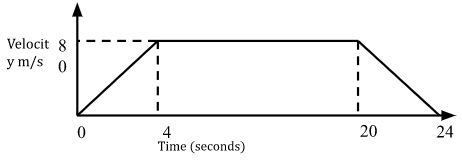
1. The figure below is a velocity time graph for a car.
  1. Find the total distance travelled by the car. (2 Mks)
  2. Calculate the deceleration of the car. (2 Mks)
2. A car left Nairobi towards Eldoret at 7.12 a.m. at an average speed of 90km/h. At 8.22 a.m, a bus left Eldoret for Nairobi at an average speed of 72km/hr. The distance between the two towns is 348km. Calculate
  1. the time when the two vehicles met. (4 Mks)
  2. the distance from Nairobi to the meeting place. (2 Mks)
Triangle PQR has vertices at P (2,3), Q(1,2) and R(4,1), while triangle PIQIRI has vertices PI(-2,3),QI(-1,2), RI(-4,1)
1. 1. Draw triangle PQR and PIQIRI on the grid provided. (2 Mks)
  2. Describe fully a single transformation which maps triangle PQR onto triangle PIQIRI. (2 Mks)
2. 1. On the same grid, draw triangle PIIQIIRII the image of PQR under a reflection on the line y + x = 0 (2 Mks)
  2. Describe fully a single transformation which maps triangle PIIQIIRII onto triangle PIQIRI. (2 Mks)
3. On the same grid, draw triangle PIIIQIIIRIII the image of PIIQIIRII under a reflection on the line x = 0 (2 Mks)
A trader bought 8 cows and 12 goats for a total of Ksh.294,000. If he had bought 1 more cow and 3 more goats he would have spend Ksh.337,500.
1. Form two equations to represent the above information. (2 mks)
2. Use matrix method to determine the cost of a cow and that of a goat. (4 mks)
3. The trader sold the animals he had bought making a profit of 40% per low and 45% per goat.
  1. Calculate the total amount of money he received. (2 mks)
  2. Determine his profit in Kenya shillings. (2 mks)
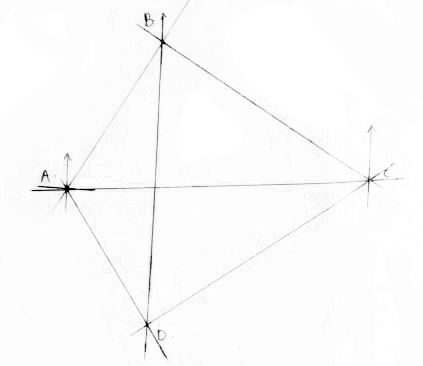
Three warships A,B and C are at the sea such that ship B is 500km on a bearing N30E from ship A. Ship C is 700km from ship B on a bearing of 120o.An enemy ship D is sighted 800km due south of ship B.
1. Taking a scale of 1cm to represent 100km, locate the positions of ships A, B, C and D.(4 mks)
2. Find the bearing of:
  1. Ship A from D (1 mk)
  2. Ship D from C (1 mk)
3. Use scale drawing to determine the distance between
  1. D and A (1 mk)
  2. C and D. (1 mk)
4. Measure angle DAC and angle BCD (2 mks)
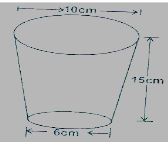
The figure below shows a tumbler with diameters 6cm and 10cm and height 15cm.
1. If it is filled with water, what area is in contact with water? (7 Mks)
2. Find the volume of the tumbler. (3 Mks)
The following are masses of 25 people taken in a clinic.

20 35 29 45 60

66 56 29 48 37

59 64 24 28 32

35 45 48 52 55

54 55 36 39 35
1. Using a class width of 8 and starting with the lowest mass of the people. Make a frequency distribution table for the data. (3 Mks)
2. Calculate the mean mass of the people. (2 Mks)
3. On the grid provided, draw a histogram and a frequency polygonto represent the information. (5 Mks)

Marking Scheme

2 + 4
1.8525 0.26153
2 (0.5396) + 4(0.3826) x 10
1.0792 + 15.304
= 16.3836
130% = 3120
100% = 100 x 3120
130
=Ksh 2400

120% = 2400
100% = 100 x 2400
120
= Ksh 2000
27 = 3 x 3 x 3
16 = 2 x 2 x 2 x 2
Area = (27 x 16)
n = 432
3 + 2
= 72 units
126 000 x 132.92
= Sh 16, 747 920
4/5 x 16, 747, 920
= 136, 398, 336
Balance
(16747920 - 136, 398, 336)
= 3,349,584
75.19
= 44548.2644 US dollars
44 548 US Dollars
x² + 4x² = 36
5x² = 36
5 5
x² = 7.2
x = 2.683281573
A= 1/2 x 8.049844719 x 5.366563146
= 21.6cm²
(x - 50) + 2x + 20 = 180
x - 50 + 2x + 20 = 180
3x - 30 = 180
3x = 180 + 30
3x = 210
3 3
x = 70°
p exterior
(70 - 50) = 20°
n = ³⁶⁰/₂₀
n = 18 sides
12x² + 9xa - 8xa - 6a²
(3x - 2a)(3x + 2a)
3x (4x + 3a) - 2a (4x + 3a)
(3x - 2a)(3x + 2a)
4x + 3a
3x + 2a
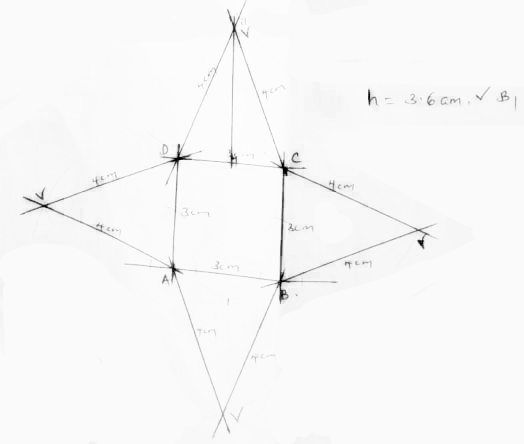
2. h = 3.6cm
1. v.s.f = ⁷⁶⁸/₃₂₄ = ⁶⁴/₂₇
  l.s.f = √(⁶⁴/₂₇) = 4/3 = 20/h
  h = 20 x 3 = 15cm
  4
2. a.s.f= (4/3)2 = 16/9
  16/9 = 40/A
  A = 40 x 9 = 23.0625cm²
  16
3a + 2 < 2a + 3
4 5
15a + 10 < 8a + 12
7d < 2
7 7
a <²/₇
2a + 3 < 4a + 15
5 6
12a + 18 < 20a + 75
-8a < 57
8 8
-a < 7.125
a= -7.125
-7.125 <a<0.2857
(-7, -6, -5,-4, -3, -2, -1, 0)
(3x + 1)(3x - 2)= 28
9x2 - 6x + 3x -2 = 28
9x2 - 3x - 30 = 0
3x2 - x - 10 = 0
3x2 - 6x + 5x - 10 = 0
3x (x-2)+ 5(x - 2)=0
(3x + 5)(x-2)=0
3x + 5 = 0
3x = 5
3 3
x = ^-5/₃
a = 2
length = (3x + 1)
(3(2) + 1)
6 + 1 = 7cm
2πrh = 1980
2 x 22/7 x 21 x h = 1980
h = 1980 = 15cm
132
V = πr²h = 22/7 x 21² x 15
20790
1000
20.81= 20.8
(x + 4) + 3x = 90
4x + 4 = 90
4x = 86
4 4
x= 21.5°
tan (x + 40°) = tan (21.5 + 40°)
tan 61.5° = 1.841770886 = 1.842
Log1025.2 = Log10(6 x 6 x 7)
10
= 2(0.7782) + (0.845) - 1
= 2.4015 - 1
=1.4015
2.521 x 10 = 25.2
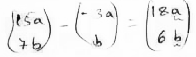
2. AC = kAB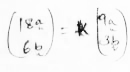
  
  K = 18a
  9a
  K= 2
  AC = 2AB
  A- common point
  Hence collinear
1. y = -4+2 = -2 = -½
  8-4 4
  y+2 = -½
  x - 8
  2y + 4 = -x+8
  2y + x - 4 =0
  x + 2y - 4 = 0
2. p(x,0)
  x + 2y - 4 = 0
  x - 4=0
  x = 4
  P(4, 0)
3. g = 2 (4, 0)
  y - 0 = 2
  x - 4
  y = 2x - 8
  Q(0,y)
  when x = 0
  y = -8
  Q (0, -8)
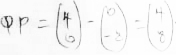
4. |QP| = √(4²+ 8²)
  = 16 + 64
  =√80
  = 8.94427191
1. original
  180,000
  n
  new
  180,000
  n-3
  180000 - 180000 = 3000
  n-3 n
  180000n - 180000n + 540000 = 3000
  n(n-3)
  540000 = 3000n² - 9000n
  n² - 3n - 180 = 0
  n² - 15n + 12n - 180 = 0
  n(n-15) + 12(n-15)= 0
  (n+12)(n -15)= 0
  n=-12 and 15
  n=15
2. 15000 - 12000 x 100%
  12000
  3000 x 100 = 25%
  12000
1. 1. A= 1/2 x 40 x 80 = 1600m
  2. a= 0-80
    4
    ^-80/₄ = 20m/s²
2. 1. Car:
    D = 90 x ⁷/₆ = 105km
    t = D/S = ^x /₉₀ = 243 - x
    72
    162x = 21870
    162 162
    x = 135
    t = 135/90 = 1.5hrs
    The time they met 7:12 + 2 hrs= 9:52am
  2. 105 + 135 = 240km
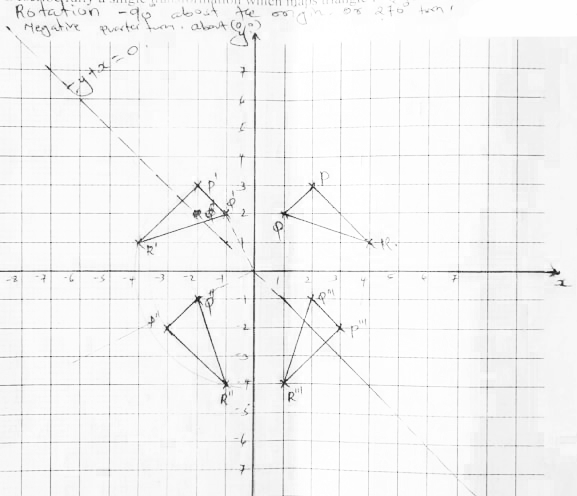
1. 2. Reflection in the x = 0/ y axis
2. 2. Rotation -90° about the origin or 270° town. Negative quarter turn about (0,0)
1. 8a + 12g = 294, 000
  9c + 15g = 337, 500
  2c + 3g = 73, 500
  3c + 5g = 112, 500
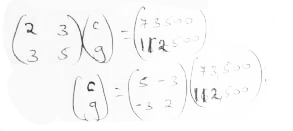
2. C = 5 (73, 500) - 3(112500)
  367500 - 337500
  C= 30,000
  g = -3(73500) + 2(112500)
  = -220, 500 + 225, 000
  = 4,500
  Cow = Sh. 30, 000
  Goat = Sh. 4, 500
3. 1. 140/160 x 30,000 = 42, 000
    145/100 x 4500 = 6525
    Total amount = 8(42000) + 12(6525)
    = (336000 + 78300) = 414300
  2. profit = 414300 - 294000 = 120,300
2. 1. 327° ± 1°
  2. 234° ± 1°
3. 1. 4.4cm ± 1= 440km
  2. 7.6 ± 1 = 760km
4. 1. <DAC = 61° ± 1°
    <BCD = 66° ± 1°
1. h + 15 = h
  5 3
  3h + 45 = 5h
  h = 22.5
  A = πRL - πrl
  L² = 37.5² + 5²
  = 1406.25 + 25
  L = 37.832
  L² = 22.5² + 3²
  = 506.25 + 9
  L= 22.699
  A= πRL - πrl
  =π (5 x 37.832 - 3 x 22.699)
  =π (189.16 - 68.097)
  = π(121.063)
  = 380.331cm²
  Area of the lower circle
  22/7 x 9 = 28.274
  Total Area = 380.331 + 28. 274 = 408.61cm²
1. Class f x fx
  
  20 - 27
  28 - 35
  36 - 43
  44 - 51
  52 - 59
  60 - 67 2
  7
  3
  4
  6
  3 23.5
  31.5
  39.5
  47.5
  55.5
  63.5 47
  220.5
  118.5
  190
  333
  190.5
  
  Σf = 25 Σfx = 1099.5
2. mean = ^Σfx/_Σf
  = ^1099.5/₂₅
  = 43.98
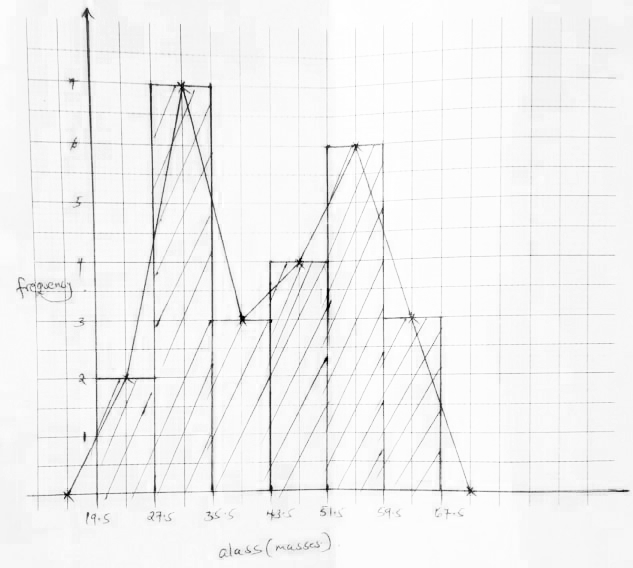
3. B1 - for correct scale and variable x and y
  B2 - for all correct bars
  B2 - for correct frequency polygon