Physics Paper 3 Questions and Answers - MECS Pre Mock Exams 2023

Instructions to Candidates

• Answer ALL questions
• You are supposed to spend the first 15 minutes of the 2 1/2 hours allowed for this paper reading the whole paper carefully before commencing the work.
• Marks are given for a clear record of the observations actually made, their suitability, accuracy and the use made of them.
• Candidates are advised to record their observation as soon as they are made.
• Non programmable silent electronic calculators may be used.
• Candidates should answer the questions in English.

For Examiner’s Use Only
Question 1

Question 2

QUESTIONS

QUESTION 1 (20 marks)
You are provided with the following apparatus;

• One dry cell and a cell holder
• One milliammeter
• A resistor labelled K
• A chain of six resistors
• A switch
• Connecting wire

Proceed as follows:
Set up the circuit as shown in Figure 1

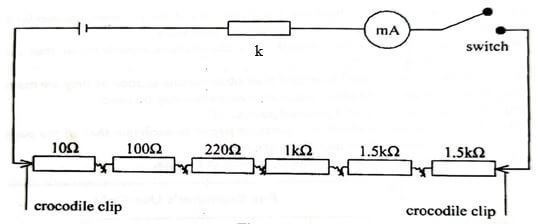
1. Switch on the circuit to obtain a positive deflection in the milliammeter. Record the reading I1 of the milliammeter. (1mk)
   I1 = ……………………………………mA
2. Remove the crocodile clips from the ends of the chains of resistors and connect them across two resistors in the resistance chain that adds up to 3.0 kΩ. Record the reading of the milliammeter, I2. (1mk)
   I2 = ……………………………………mA 

b. Repeat the procedure in (a) ii) for other values of resistance R shown in Table 1 and complete it. (6mks)
(The values of R may be obtained by combining two or more resistors in the chain)

c. Plot graph of volume, 1/I (y-axis) against R (5mks)

d. Determine the slope, S of the graph (3mks)

e. Given that the graph obeys the relationship provided in the equation
E=I(R+k)

1. Determine the value of E (2mks)
2. Determine the value of k (2mks)

QUESTION 2 (20 marks)
You are provided with the following apparatus:

• A Metre rule.
• A retort stand, boss and clamp.
• A stop watch
• An overflow can (about 180ml)
• Two 50 ml beakers labelled X and Y
• A 25ml measuring cylinder
• Two pieces of sewing thread; 30cm and100cm
• Mass labelled M
• A 250ml beaker containing about 200ml of liquid L
• A 250ml beaker with water
• Electric beam balance
• Tissue paper

PART A
Proceed as follows:

1. Using the beam balance, measure the mass of M and the mass of beaker X (2mks)
   1. Mass, M = ………………………………….
   2. Mass of beaker X, Mx = ………….……
2. Fill the overflow can with water and until overflow through the spout stops. Place the beaker X below the spout. Tie mass M with a 30 cm thread and gently immerse it into the overflow can. Wait for about one minute.
   
   
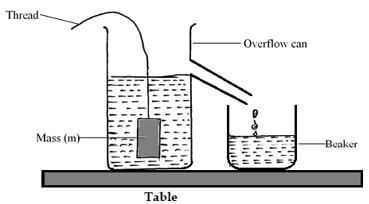
   1. Measure the mass of beaker with water and record it as M1. (1mk)
      M1 = ………………………………..
   2. Find the mass of the overflowed water in the beaker X, Mw (1mk)
      Mw = ……………………………..
   3. Pour the water in beaker X into the measuring cylinder and determine its volume. (1mk)
      V = ……………………………..
3. Remove mass M from water and empty the overflow can. Wipe to the dryness, the mass M, beaker X and the overflow can using a tissue paper. Now, place beaker Y below the spout and fill the can with liquid L until it overflows. Wait until the flow stops. Replace beaker Y with the empty beaker X, and gently immerse mass M into the liquid.
   1. After one minute, measure the mass, M2 of the beaker with liquid L. (1mk)
      M2 = ……………………………..
   2. Determine the overflowed mass ML, of the liquid L. (1mk)
      ML = ……………………………………………..
4. Determine quantity R given by (2mks)
   R=ML/Mw
   Hence, find the density of Liquid L (density of water = 1000 kgm³) (1mk)
5. Determine the density of the mass, M (2mks) 
   PART B
6. Set up the apparatus as shown in the figure below
   
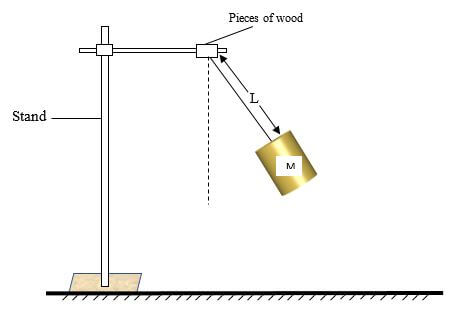
   Adjust the length L, of the thread so that L = 70cm. Displace mass M slightly so that length L makes small angle of about 100 from the vertical axis and then release it.
7. Measure and record time t, for twenty (20) oscillations. (1mk)
   t = ………………………………….
8. Repeat (g) above for 15 oscillations and 10 oscillations respectively. Record the time in the table below (3mks)
   

   Number of oscillations (n)	20	15	10
   Time, t (s)
   Periodic time, T = t/n (s)

9. Find the average periodic time, T_av (2mks)
10. Find the value of β given the equation below (2mks)
    1/(f_av )² = (4π² L)/β

MARKING SCHEME

QUESTION 1 (20 marks)
You are provided with the following apparatus;

• One dry cell and a cell holder
• One milliammeter
• A resistor labelled K
• A chain of six resistors
• A switch
• Connecting wire

Proceed as follows:
Set up the circuit as shown in Figure 1

1. Switch on the circuit to obtain a positive deflection in the milliammeter. Record the reading I1 of the milliammeter. (1mk)
   I1 = 0.27 mA
2. Remove the crocodile clips from the ends of the chains of resistors and connect them across two resistors in the resistance chain that adds up to 3.0 kΩ. Record the reading of the milliammeter, I2. (1mk)
   I2 = 0.36 mA 

b. Repeat the procedure in (a) ii) for other values of resistance R shown in Table 1 and complete it. (6mks)
(The values of R may be obtained by combining two or more resistors in the chain)

c. Plot graph of volume, 1/I (y-axis) against R (5mks)

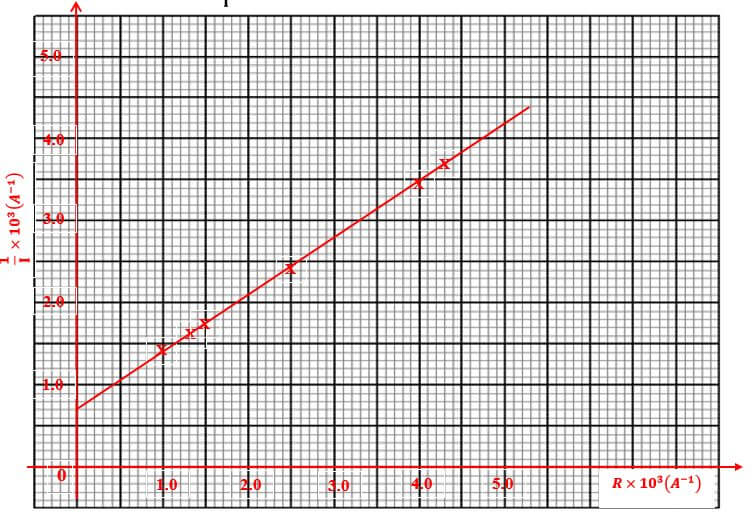
d. Determine the slope, S of the graph (3mks)

S = Δ(1/I) = (3.1 - 1.1) x 10³A^-1
       ΔR      (3.5 - 0.5) x 10³10^-1
= 2/3Ω^-1A^-1
= 0.6667Ω^-1A^-1

e. Given that the graph obeys the relationship provided in the equation
E=I(R+k)

1. Determine the value of E (2mks)
   • S = 1/E = 0.6667Ω^-1A^-1
     E =                1                 = 1.499925 AΩ
           0.6667Ω^-1A^-1
     E = 1.5 V
2. Determine the value of k (2mks)
   • 1/I-intercept=k/E
     0.7 ×10³=k/1.5
     K=1.5×700=1050 Ω

QUESTION 2 (20 marks)
You are provided with the following apparatus:

• A Metre rule.
• A retort stand, boss and clamp.
• A stop watch
• An overflow can (about 180ml)
• Two 50 ml beakers labelled X and Y
• A 25ml measuring cylinder
• Two pieces of sewing thread; 30cm and100cm
• Mass labelled M
• A 250ml beaker containing about 200ml of liquid L
• A 250ml beaker with water
• Electric beam balance
• Tissue paper

PART A
Proceed as follows:

1. Using the beam balance, measure the mass of M and the mass of beaker X (2mks)
   1. Mass, M = 100.00 g
   2. Mass of beaker X, Mx = 20.65 g
2. Fill the overflow can with water and until overflow through the spout stops. Place the beaker X below the spout. Tie mass M with a 30 cm thread and gently immerse it into the overflow can. Wait for about one minute.
   
   
   1. Measure the mass of beaker with water and record it as M1. (1mk)
      M1 = 32.63 g
   2. Find the mass of the overflowed water in the beaker X, Mw (1mk)
      Mw =

      = 32.63 – 20.65
      = 11.98 g

   3. Pour the water in beaker X into the measuring cylinder and determine its volume. (1mk)
      V =16cm³
3. Remove mass M from water and empty the overflow can. Wipe to the dryness, the mass M, beaker X and the overflow can using a tissue paper. Now, place beaker Y below the spout and fill the can with liquid L until it overflows. Wait until the flow stops. Replace beaker Y with the empty beaker X, and gently immerse mass M into the liquid.
   1. After one minute, measure the mass, M2 of the beaker with liquid L. (1mk)
      M2 = 34.95 g
   2. Determine the overflowed mass ML, of the liquid L. (1mk)
      ML = 

      = 34.95 – 20.65
      = 14.30 g

4. Determine quantity R given by (2mks)
   R=ML/Mw
   = 14.30g / 11.98 g
   = 1.194
   Hence, find the density of Liquid L (density of water = 1000 kgm³) (1mk)
   1.194 =       PL
                1000 kgm^-3
   = 1194 Kgm^-3
5. Determine the density of the mass, M (2mks) 
   • Pm = Mm = 100g
               Vm    16cm³
     = 6.25 gcm^-3 or 6250kgm^-3
     PART B
6. Set up the apparatus as shown in the figure below
   
   Adjust the length L, of the thread so that L = 70cm. Displace mass M slightly so that length L makes small angle of about 100 from the vertical axis and then release it.
7. Measure and record time t, for twenty (20) oscillations. (1mk)
   t = 33.92 s
8. Repeat (g) above for 15 oscillations and 10 oscillations respectively. Record the time in the table below (3mks)
   

   Number of oscillations (n)	20	15	10
   Time, t (s)	33.92	25.06	17.04
   Periodic time, T = t/n  (s)	1.696	1.671	1.704

9. Find the average periodic time, T_av (2mks)
   • Tav = 1.696 + 1.671 + 1.704
                               3
     = 1.690 s
10. Find the value of β given the equation below (2mks)
    1/(f_av )² = (4π² L)/β
    • 1.69 = 4 x 3.142 x 0.7
                         β
      β = 9.678 ms^-2

CONFIDENTIAL

QUESTION 1
You are provided with:

• One dry cell and a cell holder
• One milliammeter (0 - 1 mA)
• A resistor labelled k (resistance of k =1 k Ω)
• A chain of six resistors arranged as shown below.
  
• A switch
• Connecting wire 

• A metre rule.
• A retort stand, boss and clamp.
• A stop watch
• An overflow can
  (volume <180 ml. To be shared if the volume greater than 180 ml)
• Two 50 ml beakers labelled X and Y
• A 25 ml measuring cylinder
• two pieces of thread; 30cm and 100cm
• Mass labelled M
• A 250ml beaker containing 200 ml of liquid L
• A 250ml beaker with water
• Electric beam balance
• Tissue paper