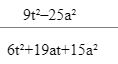Mathematics Paper 2 Questions and Answers - Form 3 Mid Term 1 Exams 2021

Share via Whatsapp

« Previous Topic
Mathematics Paper 1 Questions and Answers - Form 3 Mid Term 1 Exams 2021

Next Topic »
English Paper 1 Questions and Answers - Form 3 Mid Term 1 Exams 2021

Download PDF for future reference Get on Whatsapp for 50/-

INSTRUCTIONS

This paper consists of two sections. Answer all the questions in section 1 and any 5 questions in section 2.
KNEC mathematical tables and non-programmable calculators may be used when necessary

SECTION 1

Answer all the questions in this section

Evaluate 36 –8×–4 –15÷ –3 (3mk)
–3×–3–8(–6+ –2)
Simplify a+b – 2a–b (3mk)
2 3
Find the greatest number which divides 181 and 236 and leaves a remainder of 5 in each case (2mk)
A rectangle measures 20cm by 15cm.If each dimension is increased by 2.5cm, by what percentage is
1. the perimeter of the rectangle increased (2mk)
2. the area of the rectangle is increased (2mk)
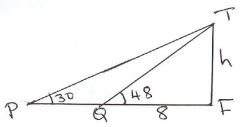
The angle of elevation of the top of a tree from a point P on horizontal ground is 30º. From another point Q 8 metres from the base of the tree, the angle of elevation of the top of the tree is 48º.
1. Calculate to one decimal place the height of the tree. (1mk)
2. Calculate the distance between P and Q (2mk)
Given that cos θ= –0.8070 , find θ for 0≤θ≤720 (3mk)
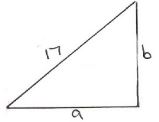
A piece of wire 40cm is bent to form a right-angled triangle whose hypotenuse is 17cm long. Find the lengths of the other two sides of the triangle (4mk)
Solve for x in log 5–2+log(2x+10)=log(x–4) (3mk)
Solve the quadratic equation by completing of squares giving your answer to 3sf (4mk)
11x² –13x+3=0
Rationalize the denominator and simplify (4mk)
4√5+3√2
2√2–√5
Use a calculator to work out
1. (1mk)
2. (1mk)
A tourist from Kenya left for Ethiopia. He exchanged sh 9898 into Ethiopian Birr at the rate of 1 Eth.Birr=ksh7.95. He spent ¾ of the money he got and converted the balance back to Kenyan money at the rate of 1Eth.Birr=ksh7.98 Calculate what he finally got to 2dp (3mk)
Simplify the expression (3mks)
Three types of tea costing sh203,sh146 and sh197 per kg are blended in the ratio of 2:5:k. Find the value of k,if the blend when sold at sh221 per kg gives 30% profit (3mk)
A two digit number is such that 4 times the units digit exceeds the tens digit by1. If the digits are reversed, the number formed is decreased by 45. Find the number. (3mk)
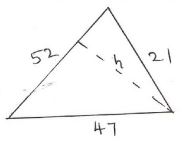
A triangular field has dimensions 21m by 52m by 47m.
1. calculate the area of the field to the nearest m². (2mk)
2. calculate the length of a straight ditch dug from the largest angle meeting the opposite side at right angles. (1mk)

SECTION 2

Answer any 5 questions in this section

A bookseller bought a number of cartons of books at a cost of ksh 57600 from Kagumo bookstore. Had he bought the same books from Kerugoya bookstore, it would have cost him ksh 480 less per carton. This would have enabled him to buy 4 extra cartons of books for the same amount of money. By taking x to be the number of cartons of books he actually bought;
1. write an expression in x
  1. for the cost of each carton he bought at Kagumo bookstore (1mk)
  2. for the cost of each carton had he bought from Kerugoya bookstore (1mk)
2. find the value of x (6mk)
3. The bookseller later sold all the books he had bought each carton at ksh 720 more than he had paid for it. Determine the percentage profit he made (2mk)
A cylindrical metal bar of diameter 14cm and length 2m is melted and moulded into spherical balls. In the process, 5% by volume of metal is lost and what remains makes balls of radius 3.5cm.
1. calculate the volume of metal used to make the balls. (3mk)
2. find to the nearest whole number the number of balls made (3mk)
3. find the total surface area of the metal bar (2mk)
4. find the total surface area of the balls made (2mk)
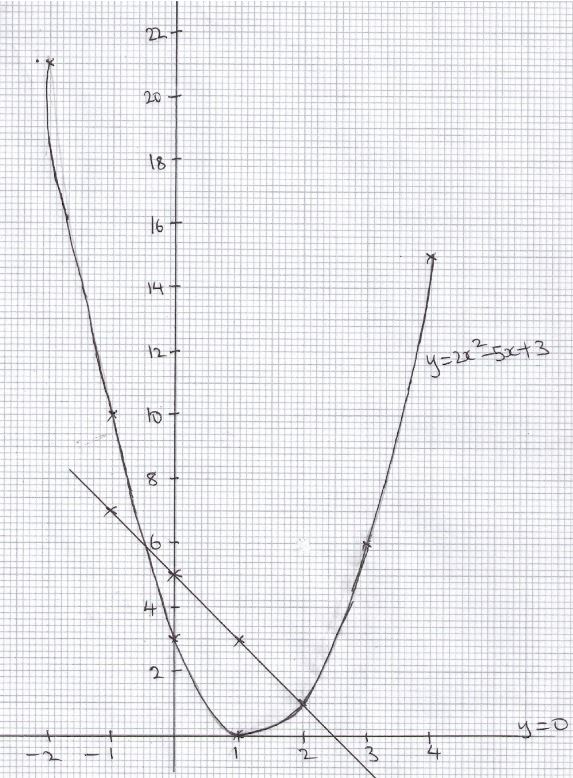
1. Draw the graph of y=(2x–3)(x–1) for the interval –2 ≤ x ≤ 4 (6mk)
2. use your graph to solve
  1. 2x²–5x+3=0 (1mk)
  2. 2x²=3x+2 (3mk)
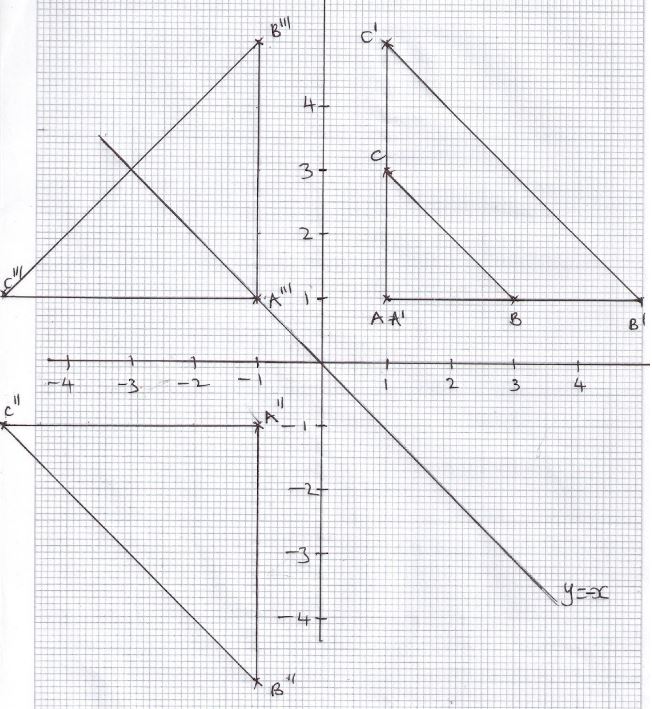
1. Plot triangle ABC with coordinates A(1, 1), B(3, 1) and C(1,3 ) (1mk)
2. Plot A′B′C′ the image of ABC under an enlargement scale factor 2 centre A and write down it’s coordinates (2mk)
3. Plot A′′B′′C′′ the image of A′B′C′ under a reflection in the line x+y=0 and write down it’s coordinates (3mk)
4. A′′B′′C′′ is then reflected in the line y=0 to give A′′′B′′′C′′′.Give the coordinates of A′′′B′′′C′′′ (2mk)
5. Describe fully a rotation that maps A′′′B′′′C′′′ onto A′B′C′ (2mk)
Three businessladies Wanjiku, Muthoni and Njoki decided to buy a lorry. The .marked price of the lorry was 2.8million shillings. The dealer agreed that the ladies could pay a deposit of 60% of the marked price and the rest to be paid within a year.The ladies raised the deposit in the ratio of 3:2:5 respectively. At the end of the year the lorry had realized 2.08million shillings which the three shared in the ratio of their contribution. However, they were required to contribute for the balance of the lorry from these earnings again in the ratio of their original contributions.
1. calculate amount to be paid as deposit (1mk)
2. how much did each contribute to pay for the deposit? (3mk)
3. how much did Njoki receive at the end of the year? (1mk)
4. calculate the total amount Muthoni and Njoki contributed to pay for the balance. (3mk)
5. how much money did Wanjiku remain with after paying her share of the balance? (2mk)
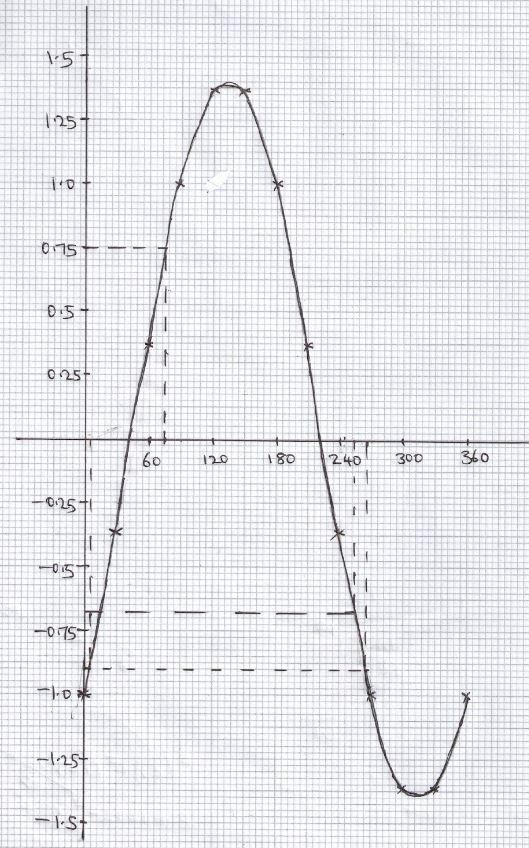
1. Make a table and draw the graph of y= sinx–cosx for x in the range 0°≤x≤360°, with y values to 2dp and x intervals of 30° (6mk)
2. use the graph to find the value of y when
  1. x=75° (1mk)
  2. x=255° (1mk)
3. find the values of x for which y= –0.9 (2mk)
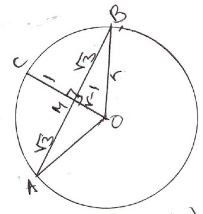
The figure below is a segment of a circle centre O radius r units.CM is the perpendicular bisector of AB.

Given that CM=1cm and AB=2√3cm,
1. calculate the radius of the circle centre O from which the segment was cut (3mk)
2. calculate the angle that chord AB subtends at the centre of the circle (2mk)
3. hence calculate
  1. the length of arc ACB (2mk)
  2. the area of the segment AMBC (3mk)
A rectangular sheet of metal which measures 120cm by 0.8m is 1.5mm thick and is made of material whose density is 2.2 g/cm³. From each of the four corners of the rectangle, a square of side 10cm is cut off and the remaining part folded to form an open cuboid.
1. calculate
  1. the capacity of the cuboid in cm³ to the nearest whole number (3mk)
  2. the mass of the empty cuboid in kg to the nearest whole number (3mk)
2. the cuboid is filled with a liquid whose density is 0.75g/cm³. Calculate the mass in kg of the cuboid when full of the liquid (2mk)
3. calculate the mass of metal lost in kg (2mk)

Marking Scheme

SECTION 1

Answer all the questions in this section

Evaluate 36 –8×–4 –15÷ –3 (3mk)
–3×–3–8(–6+ –2)
numerator 36 + 32 + 5 = 73 M1
denominator 9 − 8(−) = 9+64=73 M1
Ans ⁷³/₇₃ =1 A1
Simplify a+b – 2a–b (3mk)
2 3
3(a+b) −2(2a−b) M1
6
3a + 3b − 4a +2b M1
6
=5b − a or −a+5b A1
6 6
Find the greatest number which divides 181 and 236 and leaves a remainder of 5 in each case (2mk)
GCD of 181−5 and 236−5
= M1
The number is 11 A1
A rectangle measures 20cm by 15cm.If each dimension is increased by 2.5cm, by what percentage is
1. the perimeter of the rectangle increased (2mk)
  Original perimeter = 2(20+15) =70
  Increase = 4 × 2.5 =10 M1
  %Inc = ¹⁰/₇₀ × 100 =14.29% A1
2. the area of the rectangle is increased (2mk)
  Original area =20×15=300
  Area with increase =(2.5 +20) (2.5 + 15) = 393.75
  Increase= 93.75 M1
  %inc= 93.75 ×100 =31.25% A1
  300
The angle of elevation of the top of a tree from a point P on horizontal ground is 30º. From another point Q 8 metres from the base of the tree, the angle of elevation of the top of the tree is 48º.
1. Calculate to one decimal place the height of the tree. (1mk)
  
  Tan 48 = ^h/₈
  h = 8 tan 48 =8.885 B1
2. Calculate the distance between P and Q (2mk)
  Tan 30 = 8.885 M1
  PF
  PF = 8.885 = 15.39
  tan30
  PQ = 15.39 − 8 =7.389 A1
Given that cos θ= –0.8070 , find θ for 0≤θ≤720 (3mk)
θ = cos⁻¹ (−0.8070)
Acute θ =36.20°
2^nd & 3^rd quad
θ = 180 − 36.20 = 143.8°
θ = 180 + 36.20 =216.2°
Beyond 360° θ = 143.8 + 360 = 503.8°
θ = 216.2 + 360 = 576.2°
A piece of wire 40cm is bent to form a right-angled triangle whose hypotenuse is 17cm long. Find the lengths of the other two sides of the triangle (4mk)

a+b = 23.....(i)
a² + b² =289....(ii) M1
Substitute (i) in (ii)
a² + (23 − a)² =289
a² + 529 − 46a + a² =289
2a² − 46a + 240 =0
a² − 23a +120 =0 M1
a² − 8a − 15a + 120 = 0 M1 -Attempt to solve correctly
a(a − 8) −15(a−8) = 0
a=15 or 8
b=8 or 15 A1
Solve for x in log 5–2+log(2x+10)=log(x–4) (3mk)
log 5 − 2 log10 + log(2x+10) = log(x−4)
Log (⁵/_10²× (2x +10) ) =log(x−4)
^x/₁₀ + ½ = x − 4
⁻⁹/₁₀x = ⁻⁹/₂
x = −9 × 10
2 −9
=5
Solve the quadratic equation by completing of squares giving your answer to 3sf (4mk)
11x² –13x+3=0
x² − ¹³/₁₁ = ⁻³/₁₁x² −¹³/₁₁ + (⁻¹³/₁₁)² = ⁻³/₁₁ + (⁻¹³/₁₁)²
(x − ¹³/₁₁)² = ⁻³/₁₁+ ¹⁶⁹/₁₂₁
=¹³⁶/₁₂₁
x − ¹³/₁₁ =±√¹³⁶/₁₂₁
either x = √¹³⁶/₁₂₁ + ¹³/₁₁
=11.66 +13 =2.242
11 11
Or x = −√¹³⁶/₁₂₁+ ¹³/₁₁
=−11.66 +13 = 0.1218
11
Rationalize the denominator and simplify (4mk)
4√5+3√2
2√2–√5
(4√5+3√2)(2√2+√5)
(2√2–√5) (2√2+√5)
Num
8√10+20+12+3√10
=32+11√10
den
8+2√10 − 2√10 − 5
=3
Ans = 32+11√10
3
Use a calculator to work out
1. (1mk)
  =0.6816 B1
2. (1mk)
  =0.2030 B1
A tourist from Kenya left for Ethiopia. He exchanged sh 9898 into Ethiopian Birr at the rate of 1 Eth.Birr=ksh7.95. He spent ¾ of the money he got and converted the balance back to Kenyan money at the rate of 1Eth.Birr=ksh7.98 Calculate what he finally got to 2dp (3mk)
1 Eth. Birr =sh 7.95
? =sh 9898
=Birr 1245.03 M1
Bal after spending
=¼ × 1245.03 = 311.26 M1
1 Eth. Birr =sh7.98
311.26 = ?
=311.26 × 7.98
=sh 2483.80 A1
Simplify the expression (3mks)

num (3t−5a)(3t+5a) M1
den 6t² +9at+10at+15a²
=3t(2t+3a) +5a(2t+3a)
=(3t+5a)(2t+3a) M1
(3t−5a)(3t+5a) = 3t−5a
(3t+5a)(2t+3a) 2t+3a A1
Three types of tea costing sh203,sh146 and sh197 per kg are blended in the ratio of 2:5:k. Find the value of k,if the blend when sold at sh221 per kg gives 30% profit (3mk)
130% =221
100% = ?
=22100 =sh 170
130
2 (203) + 5 (146) + K (197) =170
7+k 7+k 7+k
406+730+197k =170(7+k)
1136+197k =1190+170k
27k = 54
k=2
A two digit number is such that 4 times the units digit exceeds the tens digit by 1. If the digits are reversed, the number formed is decreased by 45. Find the number. (3mk)
let the number be xy
4y − x =1......(i)
10x+y−(10y+x) =45
10x+y−10y−x =45
9x−9y =45......(ii) M1
From (i) x=4y−1, subst in (ii)
9(4y−1)−9y =45
36y−9−9y =45
27y = 54
y=2 M1
x = 4 × 2−1
=8−1 =7
The no. is 72 A1
A triangular field has dimensions 21m by 52m by 47m.
1. calculate the area of the field to the nearest m². (2mk)
  
  Area
  S=½(47+21+52) =60
  A= √(60(60−52)(60−47)(60−21))
  = √(60×8×13×39) =493.3m²
  =493m²
2. calculate the length of a straight ditch dug from the largest angle meeting the opposite side at right angles. (1mk)
  ½ × 52 ×h =493
  h= 493 × 2 = 18.96m
  52

SECTION 2

Answer any 5 questions in this section

A bookseller bought a number of cartons of books at a cost of ksh 57600 from Kagumo bookstore. Had he bought the same books from Kerugoya bookstore, it would have cost him ksh 480 less per carton. This would have enabled him to buy 4 extra cartons of books for the same amount of money. By taking x to be the number of cartons of books he actually bought;
1. write an expression in x
  1. for the cost of each carton he bought at Kagumo bookstore (1mk)
    57600 B1
    x
  2. for the cost of each carton had he bought from Kerugoya bookstore (1mk)
    57600 − 480 B1
    x
2. find the value of x (6mk)
  No. of cartons bought from Kerugoya bookstore = x + 4 M1
  (x + 4) ( 57600 − 480) = 57600 M1
  ( x )
  57600 − 480x + 230400 − 1920 = 57600 M1
  x
  55680x − 480x² + 230400 =57600x M1
  −1920x −480x² +230400 =0
  x² + 4x − 480 =0 M1
  x² − 20x+ 24x − 480 =0
  x( x−20) + 24(x−20) =0
  x=20
  x=−24 A1
  No of cartons = 20 B1
3. the bookseller later sold all the books he had bought each carton at ksh 720 more than he had paid for it. Determine the percentage profit he made (2mk)
  720 × 20 × 100 =25%
  57600
A cylindrical metal bar of diameter 14cm and length 2m is melted and moulded into spherical balls. In the process, 5% by volume of metal is lost and what remains makes balls of radius 3.5cm.
1. calculate the volume of metal used to make the balls. (3mk)
  ²²/₇ × 7 ×7 × 200 =30,800cm³ M1
  Remaining = ⁹⁵/₁₀₀ × 30800 M1
  = 29,260cm³ A1
2. find to the nearest whole number the number of balls made (3mk)
  ⁴/₃ × ²²/₇ × 3.5³ = volume of 1 ball
  No. of balls = 29260 × 21 M1
  4×22×3.5³
  =162.86 A1
  =162 balls B1
3. find the total surface area of the metal bar (2mk)
  2 × ²²/₇ × 7² =308
  C.S = 2× ²²/₇ × 7 ×200 =8800 M1
  T.S.A =8800 + 308
  =9108cm² A1
4. find the total surface area of the balls made (2mk)
  162 × 4 × ²²/₇ × 3.5² M1
  =24948cm² A1

Draw the graph of y=(2x–3)(x–1) for the interval –2 ≤ x ≤ 4 (6mk)
y=2x² − 2x − 3x +3
y=2x² − 5x +3

x	−2	−1	0	1	2	3	4
2x²	8	2	0	2	8	18	32
−5x	10	5	0	−5	−10	−15	−20
3	3	3	3	3	3	3	3
y	21	10	3	0	1	6	15

B1 B1 B1 S1 P1 C1

use your graph to solve
1. 2x²–5x+3=0 (1mk)
  y=0
  x=0
2. 2x²=3x+2 (3mk)
  y=2x² − 2x − 3x +3 B1
  −y=2x² − 5x +3
  0=2x² − 3x −2
  y =−2x +5
  
  x 0 −1 1
  
  y 5 7 3
  
  x=2
  y=−0.45

1. Plot triangle ABC with coordinates A(1, 1), B(3, 1) and C(1,3 ) (1mk)
2. Plot A′B′C′ the image of ABC under an enlargement scale factor 2 centre A and write down it’s coordinates (2mk)
  A′(1,1) B′(5,1) C′(1,5)
  B1 B1 B1
3. Plot A′′B′′C′′ the image of A′B′C′ under a reflection in the line x+y=0 and write down it’s coordinates (3mk)
  A′′(−1,−1) B′′(−1,−5) C′′(−5,−1)
  L1 B1 B1
4. A′′B′′C′′ is then reflected in the line y=0 to give A′′′B′′′C′′′.Give the coordinates of A′′′B′′′C′′′ (2mk)
  A′′′(−1,−1) B′′′(−1,5) C′′′(−5,−1)
  B1 B1
5. Describe fully a rotation that maps A′′′B′′′C′′′ onto A′B′C′ (2mk)
  Rotation −90° about (0,0)
  B1 B1
Three businessladies Wanjiku, Muthoni and Njoki decided to buy a lorry. The .marked price of the lorry was 2.8million shillings. The dealer agreed that the ladies could pay a deposit of 60% of the marked price and the rest to be paid within a year.The ladies raised the deposit in the ratio of 3:2:5 respectively. At the end of the year the lorry had realized 2.08million shillings which the three shared in the ratio of their contribution. However, they were required to contribute for the balance of the lorry from these earnings again in the ratio of their original contributions.
1. calculate amount to be paid as deposit (1mk)
  ⁶⁰/₁₀₀ × 2800000 = sh. 1,680,000 B1
2. how much did each contribute to pay for the deposit? (3mk)
  Wanjiku = ³/₁₀ × 1680000 =504,000 B1
  Muthoni = ²/₁₀ × 1680000 =336,000 B1
  Njoki = ⁵/₁₀ × 1680000 =840,000 B1
3. how much did Njoki receive at the end of the year? (1mk)
  ⁵/₁₀ × 2080000 = 1,040,000 B1
4. calculate the total amount Muthoni and Njoki contributed to pay for the balance. (3mk)
  bal = ⁴⁰/₁₀₀ × 2800000 = 1,120,000 M1
  ⁷/₁₀ × 1,120,000 = 784,000 M1 A1
5. how much money did Wanjiku remain with after paying her share of the balance? (2mk)
  Received = ³/₁₀ × 2080000 = 624,000
  Paid ³/₁₀ × 1120000 = 336,000 M1
  remained = 288,000 A1

Make a table and draw the graph of y= sinx−cosx for x in the range 0°≤x≤360°, with y values to 2dp and x intervals of 30° (6mk)

x	0	30	60	90	120	150	180	210	240	270	300	330	360
Sin x	0	0.5	0.87	1	0.87	0.5	0	−0.5	−0.87	−1	−0.87	−0.5	0
Cos x	1	0.87	0.5	0	−0.5	−0.87	−1	−0.87	−0.5	0	0.5	0.87	1
y	−1	−0.37	0.37	1	1.37	1.37	1	0.37	−0.37	−1	−1.37	−1.37	−1

B1 B1 B1 S1 P1 C1

use the graph to find the value of y when
1. x=75° (1mk)
  0.75 ± 0.05 B1
2. x=255° (1mk)
  0.675 ± 0.05 B1
find the values of x for which y= –0.9 (2mk)
6°, 264° ±6° B1 B1

The figure below is a segment of a circle centre O radius r units.CM is the perpendicular bisector of AB.

Given that CM=1cm and AB=2√3cm,
1. calculate the radius of the circle centre O from which the segment was cut (3mk)
  
  r²=(r − 1)² + (√3)² M1
  r² =r² − 2r + 1 + 3 M1
  2r = 4
  r=2cm A1
2. calculate the angle that chord AB subtends at the centre of the circle (2mk)
  Cos θ = ½ = 0.5
  θ =60º M1
  Angle at centre =120° A1
3. hence calculate
  1. the length of arc ACB (2mk)
    ¹²⁰/₃₆₀ × 2 × ²²/₇ ×2 =4.190 M1 A1
  2. the area of the segment AMBC (3mk)
    ¹²⁰/₃₆₀ × ²²/₇ × 2² − ½ ×2² sin 120 M1 M1
    =4.190 − 1.7321 = 2.4579 A1
A rectangular sheet of metal which measures 120cm by 0.8m is 1.5mm thick and is made of material whose density is 2.2 g/cm³. From each of the four corners of the rectangle, a square of side 10cm is cut off and the remaining part folded to form an open cuboid.
1. calculate
  B1
  1. the capacity of the cuboid in cm³ to the nearest whole number (3mk)
    99.7 × 59.7 × 9.85 M1
    =58628cm³ A1
  2. the mass of the empty cuboid in kg to the nearest whole number (3mk)
    Outer volume = 100 × 60 × 10
    = 60,000
    Inner volume =−58,628 M1
    Volume of material 1372cm³ M1
    Mass = 1372 × 2.2 =3kg A1
    1000
2. the cuboid is filled with a liquid whose density is 0.75g/cm³. Calculate the mass in kg of the cuboid when full of the liquid (2mk)
  Mass of liquid
  =0.75 × 58628 = 43.971kg M1
  1000
  Total mass = 46.971kg A1
3. calculate the mass of metal lost in kg (2mk)
  Volume = 4 × 10 × 10 × 0.15 M1
  =60cm³
  Mass = 60 × 2.2 =132g A1