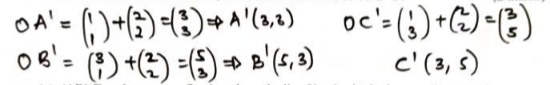Mathematics Questions and Answers - Form 3 Term 1 Opener Exams 2023

Instructions To Candidates   

• This paper has two sections: Section 1 and Section II
• Answer all questions in section I and any three questions in section II
• All answers and working must be written on the question paper in the spaces provided below each question.
• Show all the steps in your calculations, giving your answer at each stage in the space below each question.
• Marks may be awarded for correct working even if the answer is wrong.
• Non-Programmable silent electronic calculators and KNEC Mathematical Tables may be used except where stated otherwise.

SECTION I (40MKS)   
(Answer all questions from this section)

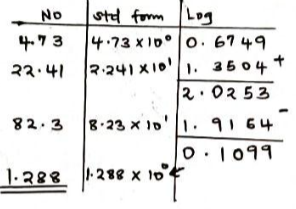
1. Use logarithms to evaluate (3mks)
   4.73×22.41
         82.3
2. Solve for x in log₃81 = x (3mks)
3. Use tables of cubes and reciprocals to evaluate (4mks)
   ²√0.498 +   0.1    
                    0.0351
4. When a number is divided by 8, 9 and 6 the remainders are 7, 8 and 5 respectively. Find the number.    (3mks)
5. A line with gradient -3 passes through (3, k) and (k, 8). Find the value of k and hence the equation of the line, where a, b and c are constants. (4mks)
6. In a fundraising committee of 45 people, the ratio of men to women is 7: 2. Find the number of women required to join the committee so that the ratio of men to women is changed to 5: 4. (3mks).
7. The marked price of a car in a dealer’s shop was Ksh. 450 000. Simiyu bought the car at 7% discount. The dealer still made a profit of 13%. Calculate the amount of money the dealer had paid for the car to the nearest thousands. (4mks)
8. The size of an interior angle of a regular polygon is 3x0 while that of exterior is (x-20)0. Find the number of sides of the polygon. (3mks)
9. The GCD and LCM of three numbers are 3 and 1008 respectively. If two of the numbers are 48 and 72, find the least possible value of the third number. (3mks)
10. A straight line through A(2, 1) and B(4, m) is perpendicular to the line whose equation is 3y = 5 − 2x. Determine the value of m. (3mks)
11. Two similar solids have surface areas of 48cm² and 108cm² respectively. Find the volume of the smaller solid if the bigger one has a volume of 162cm³. (3mks)
12. Given that cos⁡(x-20)° = sin⁡(2x+32)° and that x is an acute angle, find tan⁡(x-4)° (4mks)

SECTION II (30MKS)   
(Answer any 3 questions from this section)

13. The coordinates of a triangle ABC are A(1, 1) B(3, 1) and C (1, 3).
    1. Plot the triangle ABC. (1 mark)
    2. Triangle ABC undergoes a translation vector Obtain the image of A' B' C ' under the transformation, write the coordinates of A' B' C'. (2marks)
    3. A' B' C' undergoes a reflection along the line X = 0, obtain the coordinates and plot on the graph points A" B" C", under the transformation
       (2 marks)
    4. The triangle A" B" C" , undergoes an enlargement scale factor -1, centre origin. Obtain the coordinates of the image A'" B"' C"'. (2 marks)
    5. The triangle A"' B"' C"' undergoes a rotation centre (1, −2) angle 1200. Obtain the coordinates of the image Aiv Biv Civ. (2 marks)
    6. Which triangles are directly congruent. (1 mark)
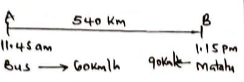
14. A country bus left town A at 11.45 am and travelled towards town B at an average speed of 60km/hr. A matatu left town B at 1.15 pm on the same day and travelled towards town A along the same road at an average speed of 90km/hr. The distance between the two towns is 540 km. Determine
    1. The time of the day the two vehicles met. (4marks)
    2. How far from town A they met. (2marks)
    3. How far from town B the bus was when the matatu reached town A (4marks)
15. The table below shows the mass to the nearest gram, of 101 mango seeds in a research station.
    

    Mass (gram)	10-14	15-19	20-24	25-29	30-34	35-39
    Frequency	2	14	33	35	14	3

    1. State the modal class. (1mark)
    2. Calculate to 2 decimal places:
       1. The mean mass (4marks)
       2. The difference between the median mass and the mean mass. (5marks)
16. A helicopter is stationed at an airport H on a bearing of 060° and 800km from another airport P. A third airport J is on a bearing of 140° and 120km from H.
    1. Using a scale of 1cm represents 100km;
       1. Show the relative positions of P, H and J (3mks)
       2. Determine the distance between P and J (2mks)
       3. State the bearing of P from J (2mks)
    2. A jet flying at a speed of 103km/h left J towards P. The helicopter at H also took off towards P at the same time. Find the speed at which the helicopter will fly so as to arrive at P 12 minutes later than the jet. (3mks)
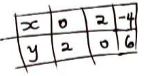
17. Given that y = 2x² + 3x − 7 for −4 ≤ x ≤ 3
    1. Complete the table below (2mks)
       

       x	−4	−3	−2	−1	0	1	2	3
       2x2	32	18				2		18
       3x		−9		−3		3	6
       −7	−7	−7	−7	−7	−7		−7	−7
       y		4	−5		−7		7

    2. Draw the graph y = 2x² + 3x − 7 for −4 ≤ x ≤ 3 (3mks)
    3. Use the graph to find the roots of the equation
       1. 2x² + 3x − 7 = 0 (2mks)
       2. 2x² + 4x − 9 = 0 (3mks)

MARKING SCHEME

SECTION I (40MKS)   
(Answer all questions from this section)

1. Use logarithms to evaluate (3mks)
   4.73×22.41
         82.3
   
2. Solve for x in log₃81 = x (3mks)
   
   3x = 81
   3x = 3⁴
   x = 4
3. Use tables of cubes and reciprocals to evaluate (4mks)
   ²√0.498 +   0.1    
                    0.0351
   (49.8 × ¹/₁₀₀)^½ +    1    
                               0.351
   7.0569 ×  1   +    1    ×     1    
                   10     3.51     10⁻¹
   0.70569 + 0.2849 ×  10
   0.70569 + 2.849
   = 3.55469
4. When a number is divided by 8, 9 and 6 the remainders are 7, 8 and 5 respectively. Find the number.    (3mks)
   Let the number be N
   ^N/₈, rem = 7
   ^N/₉, rem = 8
   ^N/₆, rem = 5
   N is given by the L.C.M of 8, 9, and 6 and subtracting 1 from it
   
   2⁸ × 3² = 72
   N = 72 − 1
       = 71
5. A line with gradient -3 passes through (3, k) and (k, 8). Find the value of k and hence the equation of the line, where a, b and c are constants. (4mks)
   8 − k = −3
   k − 3     1
   8 − k = −3k + 9
   3k - k = 9 − 8
   2k = 1
   k = ½ or 0.5
   y − ½ = − 3
   x − 3      1
   y − ½ = −3x + 9
   2y − 1 = − 6x + 18
   2y = −6x + 19
   y = −3x + ¹⁹/₂
6. In a fundraising committee of 45 people, the ratio of men to women is 7: 2. Find the number of women required to join the committee so that the ratio of men to women is changed to 5: 4. (3mks).
   Let # of wmen joining be x
   Initial # of  men
      = ⁷/₉ × 45 = 35
   Initial # of women
     = ²/₉ × 45 = 10
   After x women joined, the ratio changed to 5:4
     35    =  5 
   10+x      4
   50 + 5x = 140
      5x = 90
       x = ⁹⁰/₅
        x = 18 women 
7. The marked price of a car in a dealer’s shop was Ksh. 450 000. Simiyu bought the car at 7% discount. The dealer still made a profit of 13%. Calculate the amount of money the dealer had paid for the car to the nearest thousands. (4mks)
   ⁹³/₁₀₀ × 450000
    = 418500/=
   113% = 418500
   100% = ?
   100 × 418500
          113
    = Sh. 370000
8. The size of an interior angle of a regular polygon is 3x0 while that of exterior is (x-20)0. Find the number of sides of the polygon. (3mks)
   3x° + (x − 20°) = 180°
   4x = 180 + 20
   4x = 200°
   x = 50°
   size of exterior angle 
   = 50° − 20° = 30° 
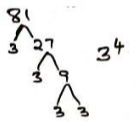
   No. of sides of polygon
9. The GCD and LCM of three numbers are 3 and 1008 respectively. If two of the numbers are 48 and 72, find the least possible value of the third number. (3mks)
   G.C.D = 3
   L.C.M = 1008
              = 2⁴ × 3² × 7
   1^st No: 48 = 2⁴ × 3
   2^nd No: 72 = 2² × 3²
   3^rd No: = 3 × 7
                = 21
   or
   3^rd No: = 3² × 7
                = 63
   Least possible # 
   = 21
10. A straight line through A(2, 1) and B(4, m) is perpendicular to the line whose equation is 3y = 5 − 2x. Determine the value of m. (3mks)
    3y − 5 − 2x
    y = ⁻²/₃x + ⁵/₃
    For  lines, m₁m₂ = −1
    m₂ = ⁻²/₃
    m₁ = ³/₂
    m − 1 = ³/₂
     4 − 2
    2m − 2 = 6
    2m = 8
     m = 4
11. Two similar solids have surface areas of 48cm² and 108cm² respectively. Find the volume of the smaller solid if the bigger one has a volume of 162cm³. (3mks)
    A.S.F = ¹⁰⁸/₄₈ = ⁹/₄
    L.S.F = √(⁹/₄) = ³/₂
    V.S.F = (L.S.F)³
    =(3/2)³
    = ²⁷/₈
    ²⁷/₈ = ¹⁶²/_x
    x = 162 × 8
               27
    x = 48cm³
12. Given that cos⁡(x-20)° = sin⁡(2x+32)° and that x is an acute angle, find tan⁡(x-4)° (4mks)
    (x − 20)° + (2x + 32)° = 90
    3x = 78
    x = ⁷⁸/₃ = 26°
    tan (x − 4)° = tan(26 − 4)°
                       = tan 22°
                      = 0.4040

SECTION II (30 MKS)   
(Answer any 3 questions from this section)

13. The coordinates of a triangle ABC are A(1, 1) B(3, 1) and C (1, 3).
    1. Plot the triangle ABC. (1 mark)
       
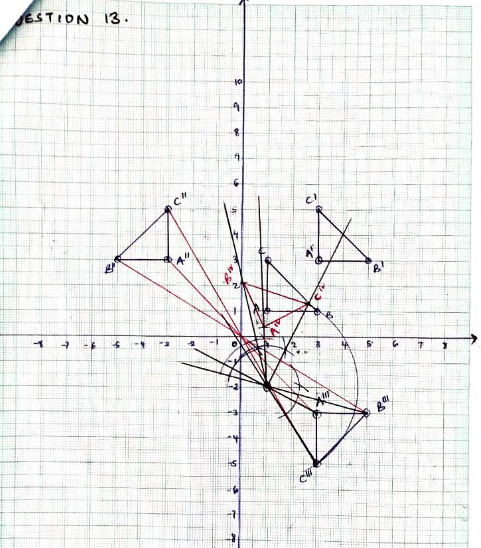
    2. Triangle ABC undergoes a translation vector Obtain the image of A' B' C ' under the transformation, write the coordinates of A' B' C'. (2marks)
       
    3. A' B' C' undergoes a reflection along the line X = 0, obtain the coordinates and plot on the graph points A" B" C", under the transformation
       (2 marks)
       A''(−3,3)          B''(−5,3)            C"(−3, 5)
    4. The triangle A" B" C" , undergoes an enlargement scale factor -1, centre origin. Obtain the coordinates of the image A'" B"' C"'. (2 marks)
       A'''(3,−3)         B'''(5, −3)          C'''(−3, 5)
    5. The triangle A"' B"' C"' undergoes a rotation centre (1, −2) angle 1200. Obtain the coordinates of the image Aiv Biv Civ. (2 marks)
       A^iv(0.9, 0.4)      B^iv(0, 2.1)          C^iv(2.6, 1.3)
    6. Which triangles are directly congruent. (1 mark)
       ABC and A'B'C'
       A'''B'''C''' and A^ivB^ivC^iv
14. A country bus left town A at 11.45 am and travelled towards town B at an average speed of 60km/hr. A matatu left town B at 1.15 pm on the same day and travelled towards town A along the same road at an average speed of 90km/hr. The distance between the two towns is 540 km. Determine
    1. The time of the day the two vehicles met. (4marks)
       
         1315
       −1145
          1.30
       Distance travelled by bus:
       60 × 1.5 = 90km
       Distnace left = 540 − 90
                            = 450km
       R.speed = 90 + 60 = 150km/h
       Time taken to meet:
       450 = 3hrs
       150
       Time of the day of meeting:
          1.15
       + 3.00     
          4.15pm
    2. How far from town A they met. (2marks)
       Bus distance: from 1.15pm
       = 60km/h × 3 hours
       = 180km
       Distance from A
       90 + 180 = 270km
    3. How far from town B the bus was when the matatu reached town A (4marks)
       Time taken by matatu
        540km  = 6 hours
        90km/h
       Distance travelled by bus from 1.15pm
         = 450km
       Distance covered in 6hrs:
       60kmk/h × 6 = 360km
       Distance of Bus from B when matatu reached A 
       450km − 360km
       = 90km
15. The table below shows the mass to the nearest gram, of 101 mango seeds in a research station.
    

    Mass (gram)	10-14	15-19	20-24	25-29	30-34	35-39
    Frequency	2	14	33	35	14	3

    1. State the modal class. (1mark)
       25 - 29
    2. Calculate to 2 decimal places:
       1. The mean mass (4marks)
          

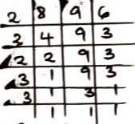
          Mass	Midpoint x	f	c.f	fx
          10-14  15-19  20-24  25-29  30-34  35-39	12   17  22  27  32  37	2  14  33  35  14   3	2   16  49  84  98  101	24  238  726  945  448  111
          		Σf = 101		Σfx = 2492

          Mean, x̄ = Σfx
                            Σf
                        = 2492
                            101
                        = 24.67g
       2. The difference between the median mass and the mean mass. (5marks)
          Median = 24.5 + (²/₃₅)5
                       = 24.5 + 0.2857
                       = 24.7857g
                       ≅ 24.76g
          Difference = 24.79 − 24.67
                           = 0.12g
16. A helicopter is stationed at an airport H on a bearing of 060° and 800km from another airport P. A third airport J is on a bearing of 140° and 120km from H.
    1. Using a scale of 1cm represents 100km;
       1. Show the relative positions of P, H and J (3mks)
          
       2. Determine the distance between P and J (2mks)
          • 8.7 ± 0.1 = 870km
       3. State the bearing of P from J (2mks)
          
          • 267°
    2. A jet flying at a speed of 103km/h left J towards P. The helicopter at H also took off towards P at the same time. Find the speed at which the helicopter will fly so as to arrive at P 12 minutes later than the jet. (3mks)
       Time taken by jet =  Distance =  870km   = 8hrs 27min
                                         speed       103km/h
       Time taken by Helicopter = 8h 27min + 12 = 8hr 39min
       S = ^D/_T 
         =    800   
             8³⁹/₆₀
         = 800 × ²⁰/₁₇₃
         = 92.5 km/h
17. Given that y = 2x² + 3x − 7 for −4 ≤ x ≤ 3
    1. Complete the table below (2mks)
       

       x	−4	−3	−2	−1	0	1	2	3
       2x2	32	18	8	2	0	2	8	18
       3x	−12	−9	−6	−3	0	3	6	9
       −7	−7	−7	−7	−7	−7	−7	−7	−7
       y	13	4	−5	−8	−7	−2	7	20

    2. Draw the graph y = 2x² + 3x − 7 for −4 ≤ x ≤ 3 (3mks)
       
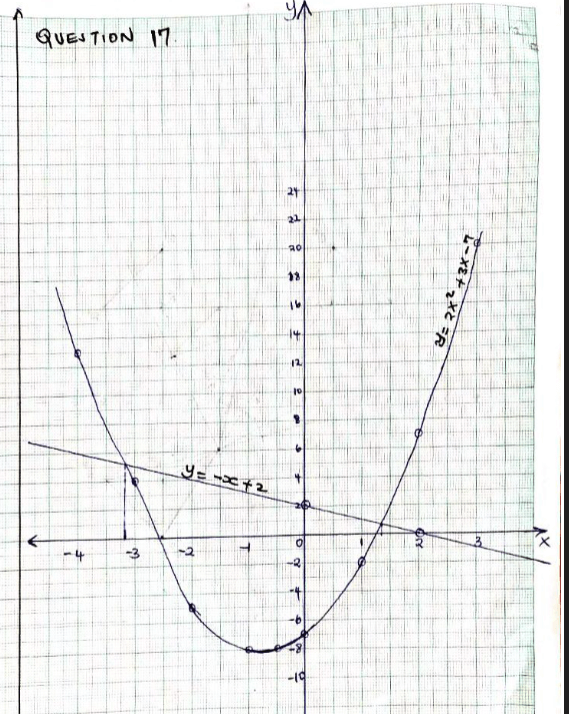
    3. Use the graph to find the roots of the equation
       1. 2x² + 3x − 7 = 0 (2mks)
          y = 2x² + 3x − 7
          0 = 2x² + 3x − 7
          y = 0
          x = −2.60 or x = 1.25
       2. 2x² + 4x − 9 = 0 (3mks)
            y = 2x² + 3x − 7
          −0 = 2x² + 4x − 9
           y =         −x + 2
          
          x = −3.2  or x = 1.3