GRADIENT AND EQUATIONS OF STRAIGHT LINES - Mathematics Form 2 Notes

• Gradient
• Equation of a Straight Line.
  • Given Two Points
  • Given the Gradient and One Point on the Line
• Perpendicular Lines
• Parallel Lines
• Past KCSE Questions on the Topic

Gradient

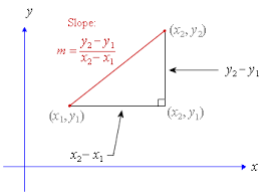
• The steepness or slope of an area is called the gradient. Gradient is the change in y axis over the change in x axis.
  
  change in y co-ordinates   =  y₂ − y₁
  change in x co-ordinates       x₂−x₁
  
  
  Note:
• If an increase in the x co-ordinates also causes an increase in the y co-ordinates the gradient is positive.
• If an increase in the x co-ordinates causes a decrease in the value of the y co-ordinate, the gradient is negative.
• If, for an increase in the x co-ordinate, there is no change in the value of the y co-ordinate, the gradient is zero.
• For vertical line, the gradient is not defined.

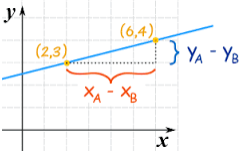
Example

Find the gradient.

Solution

Gradient = change in y axis
                 change in x axis
= 4 − 3
   6 − 2
=¹/₄

Equation of a Straight Line.

Given Two Points

Example.

Find the equation of the line through the points A (1, 3) and B (2, 8)

Solution

The gradient of the required line is 8 − 3 = 5
                                                   2 − 1
Take any point p (x, y) on the line. Using... points P and A, the gradient is y − 3
                                                                                                           x − 1
Therefore y − 3 =5
               x − 1
Hence y = 5x − 2

Given the Gradient and One Point on the Line

Example

Determine the equation of a line with gradient 3, passing through the point (1, 5).

Solution

Let the line pass through a general point (x, y).The gradient of the line is y − 5 = 3
                                                                                                          x − 1
Hence the equation of the line is y = 3x + 2

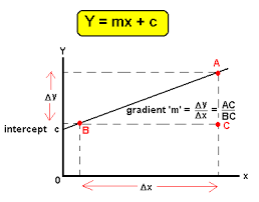
We can express linear equation in the form y = mx + c.

Illustrations.

• For example 4x + 3 y = −8 is equivalent to y= −⁴/₃x − ⁸/₃.
• In the linear equation below gradient is equal to m while c is the y intercept.
  
  
• Using the above statement we can easily get the gradient.

Example

Find the gradient of the line whose equation is 3y − 6 x + 7 =0

Solution

Write the equation in the form of y = mx + c
3y = 6x − 7
y = 2x − ⁷/₃
m = 2 and also gradient is 2.

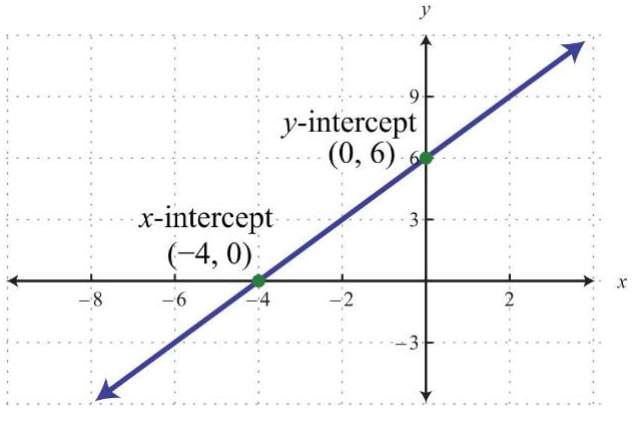
The y - intercept

• The y – intercept of a line is the value of y at the point where the line crosses the y axis. Which is C in the above figure.
• The x –intercept of a graph is that value of x where the graph crosses the x axis.
• To find the x intercept we must find the value of x when y = 0 because at every point on the x axis y = 0 .The same is true for y intercept.

Example

Find the x intercept y = 2x + 1 0 on putting y = 0 we have to solve this equation.

Solution

2x + 10 = 0
2x= −10
x =− 5
x intercept is equal to – 5.

Perpendicular Lines

• If the products of the gradient of the two lines is equal to – 1, then the two lines are perpendicular to each other.

Example

Find if the two lines are perpendicular
y = ¹/₃x +1;           y = −3x − 2

Solution

The gradients are
M= ¹/₃ and M = −3
The product is
¹/₃×−3 = − 1
The answer is -1 hence they are perpendicular.

Example

Y = 2x + 7
Y = −2x + 5
The products of their gradients is 2 × − 2 = - 4 hence the two lines are not perpendicular.

Parallel Lines

• Parallel lines have the same gradients e.g.
  y = 2x + 7
  y = 2x − 9
  Both lines have the same gradient which is 2 hence they are parallel

Past KCSE Questions on the Topic

1. The coordinates of the points P and Q are (1, −2) and (4, 10) respectively.
   A point T divides the line PQ in the ratio 2: 1
   1. Determine the coordinates of T
   2.  
      1. Find the gradient of a line perpendicular to PQ
      2. Hence determine the equation of the line perpendicular PQ and passing through T
         
      3. If the line meets the y - axis at R, calculate the distance TR, to three significant figures
2. A line L₁ passes though point (1, 2) and has a gradient of 5. Another line L₂, is perpendicular to L₁ and meets it at a point where x = 4. Find the equation for L₂ in the form of y = mx + c
3. P (5, −4) and Q (−1 , 2) are points on a straight line. Find the equation of the perpendicular bisector of PQ. Giving the answer in the form y = mx+c.
4. On the diagram below, the line whose equation is 7y – 3x + 30 = 0 passes though the points A and B. Point A on the x-axis while point B is equidistant from x and y axes. Calculate the co-ordinates of the points A and B
   
   
5. A line with gradient of -3 passes through the points (3. k) and (k.8). Find the value of k and hence express the equation of the line in the form a ax + ab = c, where a, b, and c are constants.
6. Find the equation of a straight line which is equidistant from the points (2, 3) and (6, 1), expressing it in the form ax + by = c where a, b and c are constants.
7. The equation of a line −³/₅x + 3y = 6. Find the:
   1. Gradient of the line (1 mk)
   2. Equation of a line passing through point (1, 2) and perpendicular to the given line b
8. Find the equation of the perpendicular to the line x + 2y = 4 and passes through point (2,1 )
9. Find the equation of the line which passes through the points P (3,7) and Q (6,1 )
10. Find the equation of the line whose x- intercepts is −2 and y - intercepts is 5
11. Find the gradient and y- intercept of the line whose equation is 4x – 3y