- Sector
- Area of a segment of a Circle
- Area of a Common Region Between Two Intersecting Circles.
- Past KCSE Questions on the Topic.

Sector
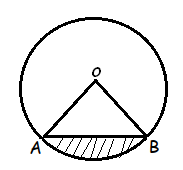
A sector is an area bounded by two radii and an arc .A minor sector has a smaller area compared to a major sector.
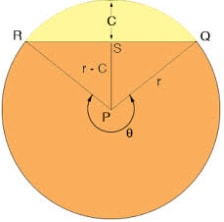
The orange part is the major sector while the yellow part is the minor sector.
The Area of a Sector
The area of a sector subtending an angle θ at the Centre of the circle is given by; A= θ/360 X πr2
Example
Find the area of a sector of radius 3 cm, if the angle subtended at the Centre is given as 1400 take π as 22/7
Solution
Area A of a sector is given by;
A= θ × πr2
360
Area= 140 x 22 x 32
360 7
= 11 cm2
Example
The area of the sector of a circle is 38.5 cm. Find the radius of the circle if the angle subtended at the Centre is 900.
Solution
From A = θ × πr2, we get
360
90/360 x22/7 x r2 = 38.5
r2 = 38.5 x 360 x 7
90 x 22
r2=49
R = 7 cm
Example
The area of a sector of radius 63 cm is 4158 cm .Calculate the angle subtended at the Centre of the circle.
Solution
4158 = θ/360 x 22/7 x 63 x 63
θ = 4158 x 360 x 7
22 x 63 x 63
= 1200

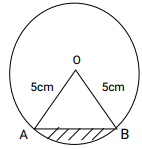
Area of a Segment of a Circle
A segment is a region of a circle bounded by a chord and an arc.
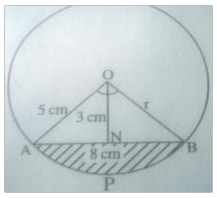
Example
In the figure above the shaded region is a segment of the circle with Centre O and radius r. AB=8 cm, ON = 3 cm, ANGLE AOB =106.30. Find the area of the shaded part.
Solution
Area of the segment = area of the sector OAPB – area of triangle OAB
=[106.3/360 × 3.142 × 52] - [1/2 × 8 × 3 ]
= 23.19 – 12
= 11.19 cm2

Area of a Common Region Between Two Intersecting Circles.
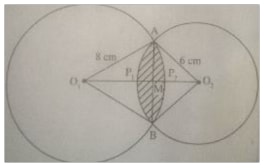
Example
Find the area of the intersecting circles above. If the common chord AB is 9 cm.
Solution
From ∆AO1M;
O1M = √(82 - 4.52)
= √43.75
=6.614 cm
From ∆AO2 M;
O2M = √(62 - 4.52)
= 15.75
=3.969 cm
The area between the intersecting circles is the sum of the areas of segments AP1B and AP2B.
Area of segment AP1B = area of sector O2AP1B - area of ∆O2AB
Using trigonometry, sin < AO2M = AM = 4.5= 0.75
AO2 6
Find the sine inverse of 0.75 to get 48.590 hence < AO2M = 48.590
∠AO2B = 2 X ∠ AO2M
= 2 X 48.590 = 97.180
Area of segment AP1B = 97.18/360 × 3.12 × 62 − 1/2 × 9 × 3.969
= 30.53 − 17.86
= 12.67 cm2
Area of segment AP2B = area of sector O1AP2B − area of ∆O1AB
Using trigonometry, sin ∠ AO1M = AM = 4.5 = 0.5625
AO1 8
Find the sine inverse of 0.5625 to get 34.230 hence ∠ AO1M = 34.230
∠AO1B = 2X∠ AO1M
= 2 X 34.230
= 68.460
Area of segment AP2B = 68.46/360 × 3.12 × 82 − 1/2 × 9 × 6.614
= 38.24 − 29.76
= 8.48 cm2
Therefore the area of the region between the intersecting circles is given by;
Area of segmnet AP1B + area of segment AP2B
= 12.67 + 8.48
= 21.15cm2

Past KCSE Questions on the Topic.
- The figure below shows a circle of radius 9cm and centre O. Chord AB is 7cm long. Calculate the area of the shaded region. (4mks)
- The figure below shows two intersecting circles with centres P and Q of radius 8cm and 10cm respectively. Length AB = 12cm
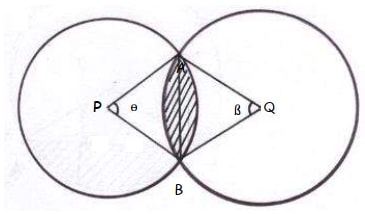
Calculate:- ∠APB (2mks)
- ∠AQB (2mks)
- Area of the shaded region (6mks)
-
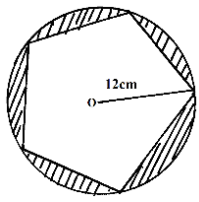
The diagram above represents a circle centre o of radius 5cm. The minor arc AB subtends an angle of 1200 at the centre. Find the area of the shaded part. (3mks) - The figure below shows a regular pentagon inscribed in a circle of radius 12cm, centre O.
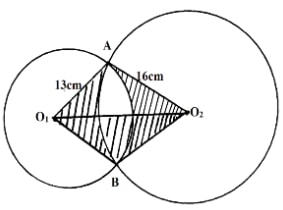
Calculate the area of the shaded part. (3mks) - Two circles of radii 13cm and 16cm intersect such that they share a common chord of length 20cm. Calculate the area of the shaded part. (π=22/7) (10mks)
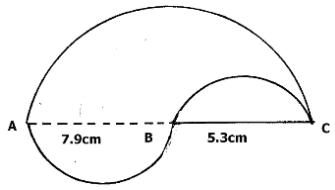
- Find the perimeter of the figure below, given AB, BC and AC are diameters. (4mks)
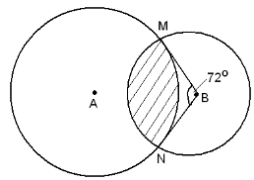
- The figure below shows two intersecting circles. The radius of a circle A is 12cm and that of circle B is 8 cm.
If the angle MBN = 72o, calculate- The size of the angle MAN
- The length of MN
- The area of the shaded region.
-
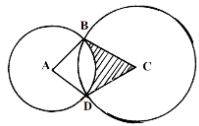
In the diagram above, two circles, centres A and C and radii 7cm and 24cm respectively intersect at B and D. AC = 25cm.- Show that angel ABC = 900
- Calculate
- the size of obtuse angel BAD
- the area of the shaded part (10 mks)
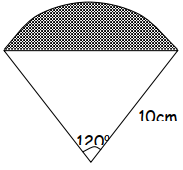
- The ends of the roof of a workshop are segments of a circle of radius 1 0m. The roof is 20m long. The angle at the centre of the circle is 120o as shown in the figure below:
- Calculate :-
- The area of one end of the roof
- The area of the curved surface of the roof
- What would be the cost to the nearest shilling of covering the two ends and the curved surface with galvanized iron sheets costing shs. 310 per square metre
- Calculate :-
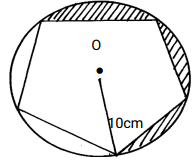
- The diagram below, not drawn to scale, is a regular pengtagon circumscribed in a circle of radius 10cm at centre O
Find;- The side of the pentagon
- The area of the shaded region
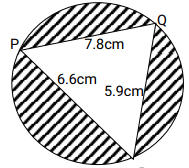
- Triangle PQR is inscribed in he circle PQ= 7.8cm, PR = 6.6cm and QR = 5.9cm. Find:
- The radius of the circle, correct to one decimal place
- The angles of the triangle
- The area of shaded region
Download Area of Part of a Circle - Mathematics Form 2 Notes.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students