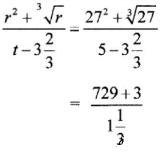KCSE 2017 Mathematics Alt B Paper 1 with Marking Scheme

Share via Whatsapp

« Previous Topic
KCSE 2017 Mathematics Alt A Paper 2 with Marking Scheme

Next Topic »
KCSE 2017 Mathematics Alt B Paper 2 with Marking Scheme

Download PDF for future reference Get on Whatsapp for 50/-

INSTRUCTIONS TO CANDIDATES

This paper consists of two sections: Section I and Section II
Answer all questions in Section I and only five questions from Section II.
Show all the steps in your calculations, giving your answer at each stage
Marks may be given for correct working even if the answer is wrong
Non-programmable silent electronic calculator and KNEC Mathematical tables may be used, except where stated otherwise
Candidates should answer the questions in English

SECTION I (50 marks)

Answer all the questions in this section in the spaces provided.

1. Express 4732 in terms of its prime factors. (1 mark)
2. Find the smallest positive number that must be multiplied by 4732 to make it a perfect square. (1 mark)
Three people Juma, Weru and Njeri went round a circular racing track, 3.12 km long. They all started from the same point and moved in the same direction. Juma walked at 48 m per minute, Weru ran at 120 m per minute while Njeri cycled at 156 m per minute.
If they started travelling at 0700 h, find the time when they were first together again. (3 marks)
Evaluate
(3 marks)
Without using a calculator, evaluate
(3 marks)
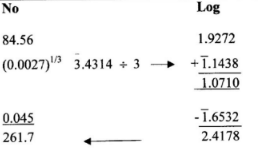
Use logarithms to evaluate:
correct to 4 significant figures. (4 marks)
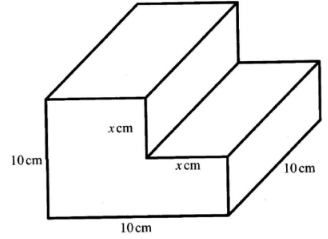
The diagram below represents a cube of side 10 cm from which a cuboid measuring xem by xcm by 10cm is removed as shown.

Write an expression in terms of x, for the surface area of the remaining solid. (3 marks)
A cylindrical tank 1.4 m in diameter contains 3234 litres of water. Find the depth, in metres, of the water. (Take π = ²²/₇ ). (3 marks)
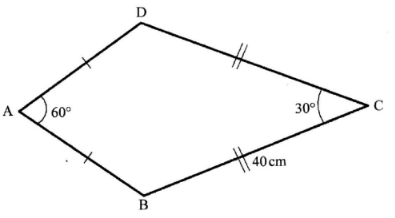
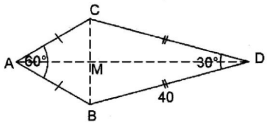
The figure below represents a quadrilateral ABCD in which angle DAB = 60°, angle BCD = 30° and BC = DC = 40cm. Side AB = AD.

Calculate the area of the quadrilateral ABCD correct to 4 significant figures. (4 marks)
The area of a sector of a circle is 36.96 cm². The sector subtends an angle of 135° at the centre of the circle. Find the radius of the circle. (Take π = ²²/₇ ) (3 marks)
Evaluate the expression given that t=5 and r = 27. (2 marks)
Two employees Njoka and Okoth contributed ¼ and ¹/₆ of their salaries respectively to start a project The contribution amounted to Ksh 16 000. If Njoka contributed ⁴/₉ and Okoth ¹/₃ of their salaries, the contribution would have been ksh 30 000. Calculate each person's salary. (3 marks)
Solve x − 8 ≤ − x ≥ 4 −3x and represent the integral values of x on a number line. (4 marks)
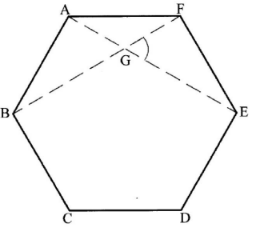
Figure ABCDEF is a regular hexagon. Line AE and BF intersect at G.

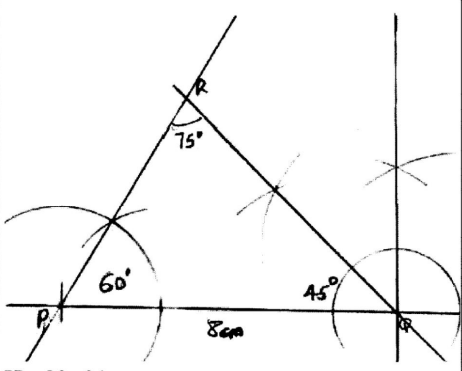
Find the size of angle FGE. (3 marks)
Using a ruler and a pair of compasses only, construct triangle PQR in which PQ = 8 cm, ∠RPQ = 60° and ∠PRQ = 75°. Measure PR. (4 marks)
The marked price of a TV set is Ksh 36000. A dealer sold the set and allowed a 12% discount on the marked price and still made a 25% profit on the cost price. Find the cost price of the set. (3 marks)
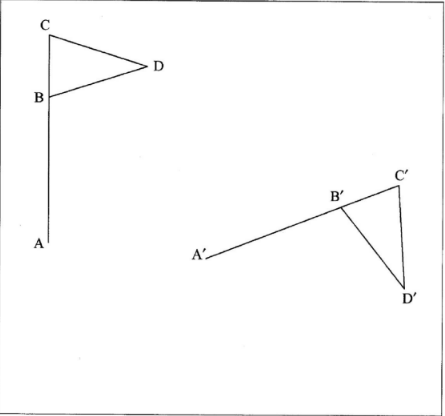
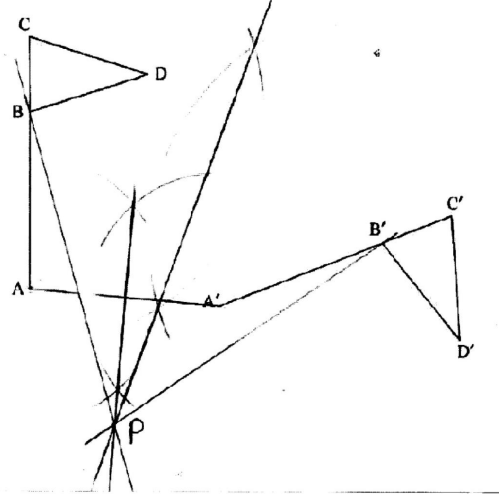
Figure A'B'C'D' is the image of ABCD under a rotation. By construction, determine the centre P and the angle of rotation. (3 marks)

SECTION II (50 marks)

Answer any five questions in this section in the spaces provided

A saleslady earns a monthly salary of Ksh 60 000. She gets a commission of 4% on the value of goods she sells above Ksh 250 000 but less than Ksh 400 000. On goods sold above Ksh 400 000, she gets a commission of 7.5%.
1. In a certain month, she sold goods worth Ksh 525 000. Calculate her total earnings that month. (4 marks)
2. In another month, she earned a total of Ksh 94 500. Find the value of goods that she sold that month.
  (6 marks)
Lines y + 2x = 4 and 3x − y = 1 intersect at point T.
1. Find the equation of line L, which passes through point T and (3,−2). (5 marks)
2. A line L₂ passes through (5,4) and is parallel to L₁ Find the equation of L₂ in the form y=mx+c where m and care constants. (2 marks)
3. Another line is L₃ perpendicular to L₁ at T. Find the equation of L₃ in the form ar + by = c where a, b and care integers. (3 marks)
A car travelled from town A to town B. The car started from rest at A and moved with a constant acceleration for 2 minutes and attained a speed of 1.2 km/minute. It then maintained this speed for a further 10 minutes before decelerating at a constant rate for another four minutes. The car finally came to rest at B.
1. On the grid provided, draw a speed-time graph for the car. (4 marks)
2. Use the graph to calculate:
  1. the distance, in metres, the car travelled during its deceleration; (2 marks)
  2. the distance, in kilometres, covered by the car in the whole journey; (2 marks)
  3. the average speed, in km/h, for the whole journey. (2 marks)
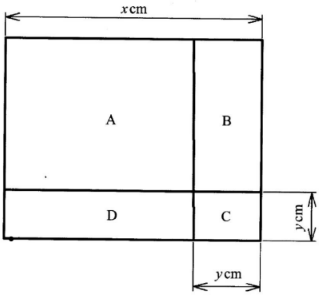
The figure below is a square of side x cm. The square is divided into four regions A, B, C and D. Regions A and Care squares. Square C is of side yem. Regions B and D are rectangles.
1. Find the total area of the following regions in terms of x and y in factorised form:
  1. A and C; (1 mark)
  2. B and D; (2 marks)
  3. A, B, C and D. (2 marks)
2. Find the total area of B and D in terms of x given that y = 2 cm. (2 marks)
3. Factorise 25c² − 16. Evaluate without using mathematical tables:
  1. 5024² − 4976² (1 mark)
  2. 8.96² − 1.04² (1 mark)
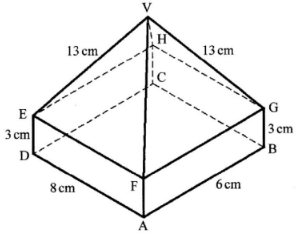
The figure below represents a right pyramid VEFGH mounted on a cuboid ABCDEFGH. Line AB = 6 cm, DA = 8 cm and AF = BG = CH = DE = 3 cm. Line VE = VF = VG = VH = 13 cm.

Calculate, correct to 2 decimal places:
1. the surface area of the rectangular faces; (3 marks)
2. the surface area of the triangular faces. (5 marks)
3. the total surface area of the solid. (2 marks)
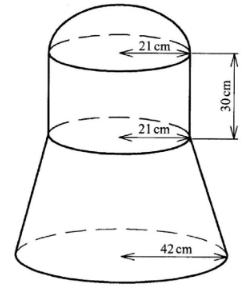
The figure below is a solid which consists of a frustum of a cone, a cylinder and a hemispherical top. The internal radii of the frustum are 42 cm and 21 cm. The vertical height of the original cone was 40 cm and the height of the cylinder is 30 cm.

Calculate:
1. the volume of the frustum part; (5 marks)
2. the volume of the cylindrical part; (2 marks)
3. the total volume of the solid. (3 marks)
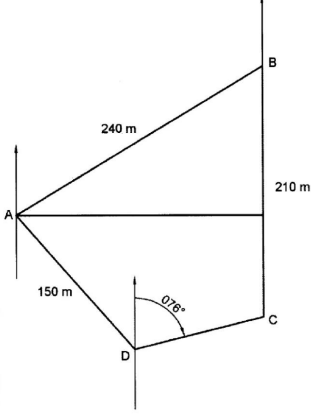
Four posts A, B, C and D stand on a level horizontal ground. Post B is 240 m on a bearing of 060° from A, C is 210m to the south of B and D is 150 m on a bearing of 140° from A.
1. Using a scale of 1 cm to represent 30m, show the relative positions of the posts. (4 marks)
2. Use the scale drawing to:
  1. find the distance and the bearing of C from D; (2 marks)
  2. determine how far A is to the west of B. (2 marks
3. The height of post D is 18m. Calculate, correct to 2 decimal places, the angle of elevation of the top of post D from the foot of post A. (2 marks)
The vertices of a triangle are A(-2, 2), B(2, 2) and C(2,8).
1. On the grid provided, draw triangle ABC and its image A'B'C' under a rotation of −90° about R(1,1).
  (3 marks)
2. The vertices of triangle A"B"C"are A"(-1,-5), B"(-1, -3) and C"(-4,-3).
  1. Draw triangle A"B"C". (1 mark)
  2. Describe fully the transformation X that maps Δ A'B'C' onto Δ A"B"C". (3 marks)
3. Triangle A'''B'''C''' is the image of triangle A"B"C" under a reflection in the line x = 0. On the same grid, draw triangle A"B""C"". (1 mark)
4. State the type of congruence between: (1 mark)
  1. ΔABC and ΔA'B'C'. (1 mark)
  2. Δ A''B''C'' and Δ A''' B''' C ''' (1 mark)

MARKING SCHEME

1. 4732 = 2² × 7 × 13²
2. 2² × 7 × 13² × 7 = 2² × 7² × 13² is a perfect square.
  ∴ smallest factror is 7
Time taken : Juma 3120 = 65 min
48
Weru 3120 = 26 min, Njeri = 3120 = 20min
120 156
LCM of 65, 26, 20

LCM = 260min or 4h 20min
Time together is 1120h
= −10
−5
= 2
= ³³/₂₀ × ⁵/₁₁
= ³/₄
4 × 10 × 10 + 2 × (10 × 10 − x²)
= 400 + 200 − 2x²
= 600 − 2x²
²²/₇ × 0.7 × 0.7 × h = 3.234
1.54h = 3.234
h = 3.234
1.54
= 2.1m
Area of ΔABC
Area of ΔBDC
BM = sin 15° ⇒ BM = 40 sin 15°
BC = 2 × 40 sin 15°
= 20.71cm
Area of the qusdrilateral
=½ × (20.71)² × sin 60 + ½ × 40² × sin 30
=185.7 + 400
=585.7cm²
¹³⁵/₃₆₀ × ²²/₇ × r² = 36.96
r² = 36.96 × 360 × 7
135 × 22
r = √31.36
= 5.6cm
=549
Let Njoka's salary be x, and Okoth's salary be y
¼x + ¹/₆y = 16000
⁴/₉ x + ¹/₃y = 30000
3x + 2y = 192000
4x + 3y = 270000
9x + 6y = 576000
8x + 6y = 540000
x = 36000
y =42000
Njoka's sh.36000 and Okoth's sh 42000
x − 8 ≤ − x −x ≥ 4 −3x
2x ≤ 8 2x ≥ 4
x ≤ 4 x ≥ 2
2 ≤ x ≤ 4
∠BAF = 120° interior angle of a regular hexagon
∠AEF = ∠FAE = 180 − 120 = 30°
2
In ΔEFG, ∠EFG = 120 − 30 = 90°
∴ ∠FGE = 180 − (90+30) = 60°
PR = 5.9 ± 0.1cm
Sellinig price was Ksh 36000 × ⁸⁸/₁₀₀
= Ksh 31680
Cost price was ksh31680 × ¹⁰⁰/₁₂₅
= Ksh 25344
Centre P
Angle of rotation, −71°
1. ⁴/₁₀₀ × (400000 − 250000) + ^7.5/₁₀₀ × (525000 − 400000) + 60000
  =6000 + 9375 + 60000
  =Ksh 75375
2. 94500 = 60000 + 6000 + x
  x = 28500
  Value of goods for commission of ksh 28500
  = 28500 × 100
  7.5
  = Ksh 380000
  Total sale = 250000 + 150000 + 380000
  = ksh 780000
1. y + 2x = 4
  −y =3x = 1
  5x = 5
  x = 1
  y + 2 = 4 ⇒ y = 2
  T(1,2)
  Grad
  −2−2 = −4 = −2
  3−1 2
  y − 2 = −2
  x − 1
  y = − 2x + 4
2. Grad = −2
  y − 4 = −2
  x − 5
  ⇒ y − 4 = −2x + 10
  y = −2x +14
3. Grad = ½
  y − 2 = ½
  x − 1
  y − 2 = ½(x − 1)
  2y − 4 = x − 1
  −x + 2y = 3
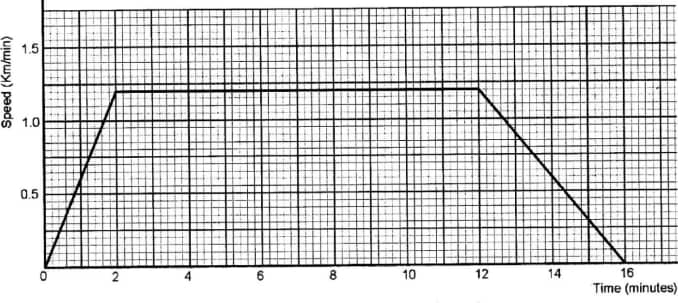
1. Scale
  Acceleration part
  Constant acceleration
  Deceleration
2. 1. ½ × 4 × 1.2 × 1000m
    =2400
  2. ½ × 2 × 1.2 + 1.2 × 10 + ½ × 4 × 1.2km
    =15.6km
  3. Average speed
    =
    =58.5km/h
1. 1. Area of A + C = (x − y) (x − y) + y²
  2. Area of B + D = y(x − y) + y(x − y)
    =2y(x − y)
  3. (x − y)² + y² + 2y(x − y)
    =(x − y)(x − y) + y² + 2yx − 2y²
    =x² − 2yx + y² + y² + 2yx − 2y²
    =x²
2. 2(x−2) +2(x−2)
  =4x − 8
3. 25c² − 16 = (5c)² − 4²= (5c+4)(5c−4)
4. 1. 5024² − 4976² = (5024 + 4976)(5024 − 4976)
    =10000 × 48
    =480000
  2. 8.96² −1.04² = (8.96 + 1.04)(8.96 − 1.04)
    = 10 × 7.92
    =79.2
1. Area of the base of the cuboid
  = 8 × 6cm² = 48cm²
  Area of 4 faces of the side of th cuboid
  =(2×8×3+2×6×3)cm²
  =48+36cm = 84cm²
  Total 48+84 = 132cm²
2. Consider faces VEF and VHG use Hero's formula
  S = ½(13+13 + 8) = 17cm
  Area of VEF and VHG = 2√(17(17−13)(17−13)(17−8))cm
  = 2√(17x4x4x9) = 98.96cm
  Consider faces VFG and VEH
  S =½ (13+13+6)=16cm
  Area of VFG
  = 2√(16(16−13)(16–13)(16 −6))
  = 2√(16 x 3 x 3 x 10)
  =75.90cm²
  Area of triangular faces
  98.96+75.90
  = 174.86cm²
3. Surface area of the solid
  =132+174.86
  =306.86cm²
1. Vertical height of small cone:
  AE = 21 ⇒ AE = 20cm
  Volume of frustum
  ¹/₃ × ²²/₇ × 42² x 40 – ¹/₃ × ²²/₇ × 21² × 20
  = 73920 − 9240
  = 64680cm³
2. Volume of cylindrical part
  = ²²/₇ x 21² x 30
  = 41580 cm²
3. Volume of hemispherical part
  ½ × ⁴/₃ × ²²/₇ × 21³
  =19404cm²
  Total volume
  = 64680+41580+19404
  =125 664 cm²
2. 1. Distance CD = 3.7 × 30
    =111km
    Bearing of C from D = 076°
  2. Distance of A to the west of B
    =6.9 × 30
    =207km
3. tan θ = ¹⁸/₁₅₀
  =0.12
  θ = tan⁻¹ 0.12
  =6.84°
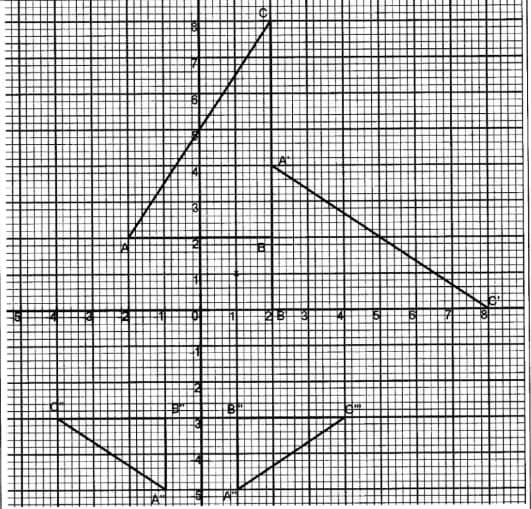
1. Δ ABC correctly drawn
  A'B'C' correctly plotted
  Δ A'B'C' drawn
2. 1. Δ A"B"C" drawn enlargement
  2. scale factor, −½ centre (0, −2)
3. Δ A'''B'''C''' drawn
4. 1. Directly congruent
  2. Opposite congruent