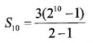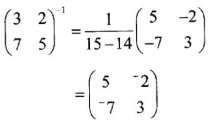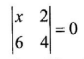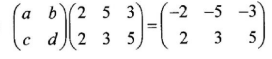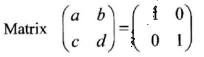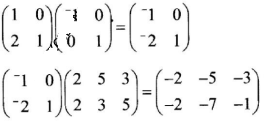KCSE 2017 Mathematics Alt B Paper 2 with Marking Scheme

SECTION I (50 marks)
Answer all the questions in this section in the spaces provided.

1. Evaluate 190.1 X 30, correct to 3 significant figures. (2 marks)
2. Find the sum of the first 10 terms in the Geometric Progression 3, 6, 12, ...   (3 marks)
3. Given that 5, x, 35 and 84 are in proportion, find the value of x.   (3 marks)
4. The base of a triangle is 3 cm longer than its height and its area is 35 cm². Determine the height and base of the triangle.  (4 marks)
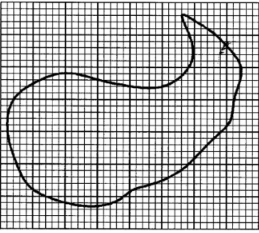
5. The figure below is a map of a piece of land on a grid of 1 cm squares.
   
   Estimate the area of the map in square centimetres.  (3 marks)
6. A chord of a circle, radius 5 cm, subtends an angle of 30° at the centre of the circle. Determine the length of the chord, correct to 2 decimal places.  (3 marks)
7. The extension (E), in cm, of a rubber band when pulled by a force (F) was found experimentally and recorded as shown in the table below:
   

   Force (F)	0	2	4	6	8
   Extension (E)	0	3	6	9	12

   1. On the grid provided, draw a graph of extension(E) against force(F). (2 marks)
   2. Use the graph to determine the extension when the force is 7 units.   (1 mark)
8. The position of towns M and N are M(0°, 51°W) and N(0°, 37°E). Find the distance between the two towns in kilometres, correct to one decimal place. (Take the radius of the earth as 6370km and  π = ²²/₇ )  (3 marks)
9. The table below shows the values of y = 2sin(θ+ 30°) for 0° ≤ θ ≤ 360°.

   θ

   0°

   30°

   60°

   90°

   120°

   150°

   180°

   210°

   240°

   270°

   300°

   330°

   360°

   y = 2sin(θ+ 30°)

   1

   1.7

   2

   1.7

   1

   0

   −1

   −1.7

   −2

   −1.7

   −1

   0

   1

   
   
   1. On the grid provided below, draw the graph of y = 2sin(θ+30°) for 0° ≤ θ ≤  360°. Use 1 cm for 30° on the x-axis and 2 cm for one unit on the y-axis.   (3 marks)
   2. Use the graph to determine the value of y when θ= 162°.  (1 mark)
10. The figure below represents the distance covered by a car within a given period of time.
    
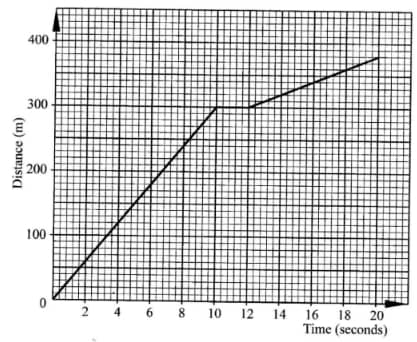
    Find the average speed of the car in kilometres per hour   (3 marks)
11. Kitonga deposited Ksh 50000 in a bank which paid compound interest at the rate of 10% per annum. Find the compound interest accrued by the end of the fourth year.   (3 marks)
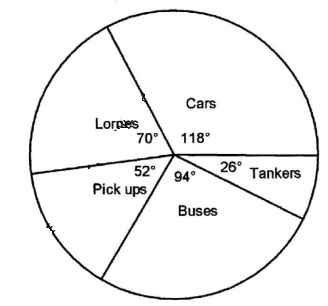
12. The number of different vehicles allowed through a road block was recorded as follows:
    

    Type of vehicles	Cars	Lorries	Pick-ups	Buses	Tankers
    No. of vehicles	59	35	26	47	13

    Represent the above data in a pie chart.  (3 marks)
13. Somi bought 2 pencils and 3 rubbers for Ksh 60 from a certain shop. Miheso bought I pencil and 2 rubbers for Ksh 35 from the same shop. Find the price of one pencil and that of one rubber.  (3 marks)
14.  
    1. Find a matrix which, when multiplied by matrix M = gives the identity matrix.  (2 marks)
    2. Given that N = is a singular matrix, find the value of x.  (2 marks)
15. A square QRST with vertices Q(1,1), R(3,1), S(3,3) and T(1,3) is transformed by the matrix  to Q'R'S'T'. Find
    1. the area of square QRST;   (2 marks)
    2. the area of image Q'R'S'T'.  (2 marks)
16. Given that p = 6i+2j, determine the magnitude of p, correct to 2 decimal places.   (2 marks)

SECTION II (50 marks)

Answer any five questions from this section in the spaces provided

17. The second term of an arithmetic progression(AP) and fourth term of a geometric progression(GP) are each 80. The sixth terms of the AP and GP are each 320.
    
    1. Find:
       
       1. the first term and the common differences of the AP.   (2 marks)
       2. the first term and the common ratio of the GP.   (2 marks)
    2. Determine the 20^th term of the AP. (2 marks)
    3. Determine the difference between the sum of the first 12 terms of the GP and the sum of the first 12 terms of the AP.   (4 marks)
18.  
    1.  
       1. Complete the table below for the values of y = x² − x − 6 for −3 ≤ x ≤ 4.  (2 marks)
          

          x	−3	−2	−1	0	1	2	3	4
          y = x2 − x − 6

       2. Find y when x = ½ (1 mark)
    2. On the grid provided, draw a graph ofy = x² − x − 6 for −3 ≤ x ≤ 4. (3 marks)
    3. On the same grid, draw line y = ⁻³/₂x + 1  and hence solve the equation x² − x − 6 = ⁻³/₂x + 1  (4 marks)
19. The marked price of a wall unit was Ksh 50 000. The price on hire purchase (HP) terms was 175% of the marked price.
    1. A customer bought the wall unit in cash and was offered 10% discount. Find the amount of money the customer paid for the wall unit.  (2 marks)
    2. A second customer decided to purchase a similar wall unit on HP terms.
       1. Determine the HP price.  (2 marks) 
       2. The customer paid 20% of the HP price as deposit and was to pay the balance in 28 equal monthly instalments. Find the amount of each monthly instalment.   (3 marks)
    3. A third customer bought a similar wall unit in cash by taking a loan equal to the marked price. The loan was to be repaid in 15 months and the bank charged interest at the rate of 4% compounded monthly. 
       1. Find, correct to the nearest shilling, the amount of money the third customer paid the bank. (2 marks)
       2. Find the amount of money the third customer spent more than the marked price.  (1 mark)
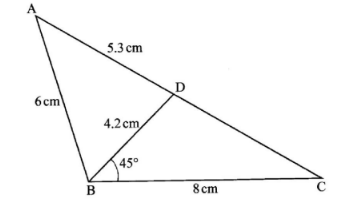
20. The figure below shows triangle ABC in which AB = 6 cm, BC = 8 cm, BD = 4.2 cm and AD = 5.3 cm. Angle CBD = 45°.
    
    Calculate, correct to one decimal place:
    1. the length of CD;   (3 marks)
    2. size of angle ABD;   (3 marks)
    3. size of angle BCD;    (2 marks)
    4. area of triangle ABD.    (2 marks)
21. Mawira, a poultry farmer carried out the following transactions during the month of February 2017:
    February 1: Had Ksh 10000 carried forward from January 2017
                  3: Bought 2 bags poultry feed @Ksh 1250
                  7: Paid Ksh 750 for water
                11: Bought materials for construction for Ksh 1900
                13: Received Ksh 12000 from sale of broilers
                17: Sold 500 eggs at Ksh 8 each
                21: Paid wages to 2 casuals at Ksh 1 750 each
                24: Sold chicks for Ksh 5000
                25: Paid Ksh 1 300 for electricity
                26: Sold 30 layers at Ksh 500 each
                28: Bought incubator for Ksh 12 500
    Prepare a single column cash book for Mawira's transactions and balance it as at 1^st March 2017.  (10 marks)
22. The table below shows the marks of 50 candidates in a test.
    

    Marks	1-10	11-20	21-30	31-40	41-50	51-60	61-70	71-80	81-90	91-100
    Frequency	2	4	5	8	11	9	5	3	2	1

    1. Draw a cumulative frequency curve for the data.   (5 marks)
    2. Use the graph to determine:
       1. the median mark;  (2 marks)
       2. the percentage of students who scored above 64%.   (3 marks)
23. Two boxes B and C contain identical balls except for the colour, Box B contains 5 violet balls and 3 green balls. Box C contains 3 violet balls and 4 green balls.
    1. A ball is drawn at random from each box. Find the probability that both balls are of the same colour. (4 marks)
    2. Two balls were drawn at random from each box, one ball at a time without replacement. Find the probability that:
       1. the two balls drawn from box B or box C are violet;  (4 marks)
       2. all the four balls drawn are violet.   (2 marks)
24. The vertices of a triangle ABC are A(2, 2), B(5, 3) and C(3,5).
    1. Find the vertices of Δ A'B'C' the image of Δ ABC under the transformation represented by the matrix 
       (2 marks)
    2. Triangle ABC is mapped onto Δ A"B"C" whose vertices are A"(-2,2), B"(-5, 3) and C"(-3, 5). Find the matrix of this transformation.  (4 marks)
    3. Triangle ABC undergoes two successive transformations PQ =  
       Determine the vertices of ΔA'"B'"C'", the image of ΔABC, under the combined transformation   (4 marks)

MARKING SCHEME

1. 190.1 × 30 = 5703
   = 5700
2. Common Ratio: ⁶/₃ = 2
   
   =3(1024−1) = 3069
            1
3. ⁵/_x = ³⁵/₈₄ 
   x = 5 × 84
            35
     = 12
4. Let height be x cm
   ½(x+3)x = 35
   x² + 3x − 70 = 0
   (x+10)(x−7)=0
   x = 7 or x = −10
   ∴ height = 7, base 7 + 3 =10
5. Full square = 11
   Fractional square = 26
   Area estimate: 11 + ²⁶/₂
                       = 24cm²
6. Let length be x
      x        =    5     
   sin 30°      sin 75°
   x = 5 sin 30°
          sin 75°
   x = 2.59
7.  
   1.  
      
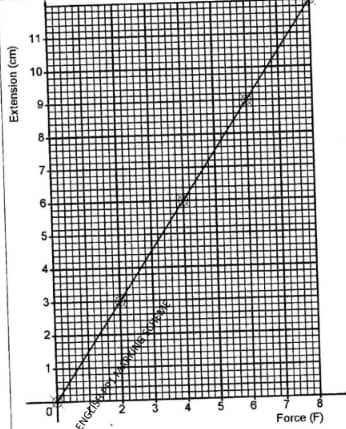
   2. Extension when force is 7 units 10.5cm
8. Latitude difference 51° + 37° = 88°
   Distnac in kilometres;
   = ⁸⁸/₃₆₀ × ²²/₇ × 2 × 6370
   =9787.6
9.  
   1.  
      
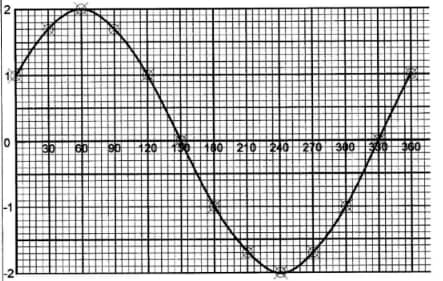
   2. When θ° = 162°, y = 0
10. Distance covered 380m
    Time taken  20s
    ∴ speed = 380  ÷   20   
                   1000     3600
                = 380  ×   3600   
                   1000        20
                = 68.4km/h
11. Compound interest by end of 4^th year
    = 50 000x 1.1⁴ − 50 000
    = 50 000(1.1⁴ − 1)
    = 50 000(1.4641−1)
    = 50 000 (0.4641)
    =Ksh 23 205
12. Angle representing different vehicles:
    Cars = ⁵⁹/₁₈₀ × 360 =118°
    Lorries = ³⁵/₁₈₀ x 360 = 70°
    Pickups =  ²⁶/₁₈₀ X 360 =52°
    Buses = ⁴⁷/₁₈₀ x 360 =94°
    Tankers = ¹³/₁₈₀ X 360 = 26°
    
13. 2p+ 3r=60.............(i)
    1p+ 2r = 35 ............(ii)
    2p+4r = 70............... (iii)
    (iii) − (i)
    r = 10
    1p+ 2(10) = 35
    p= 15
    rubber is sh10 and pencil is sh35
14.  
    1.  
       
    2.  
       
       4x − 12 = 0
       x = 3
15.  
    1. Side of QRST = √(1−1)² + (3−1)²
                           = 2
       ∴ Area = 2 × 2 = 4
    2. Area of Q'R'S'T'
       = det. 
       = 6 × 4 
       =24
16. l9l = √(6² +2²)
    = √40 = 6.32
17.  
    1.  
       1. a+d=80
          a + 5d = 320
          4d=240
          d = 60
          a = 20 
       2. ar³ = 80...............(i)
          ar⁵ = 320.............(ii)
          r² = 320 = 4
                  80
          r = 2
          a = ⁸⁰/₈ = 10
    2.  A.P.T₂₀ = 20 + 19 × 60
                    = 1160
    3. G.P.S₁₂  =
                   = 49140
       A.P.S₁₂ = ¹²/₂(2 × 12 + (12 − 1)60)
                   =4104
       Differences = 49140 − 4104
                        = 45 036
18.  
    1.  
       1.  
          

          x	−3	−2	−1	0	1	2	3	4
          y = x2 − x − 6	6	0	−4	−6	−6	−4	0	6

       2. y = (½)² − ½ − 6 =−6.25
    2.  
       
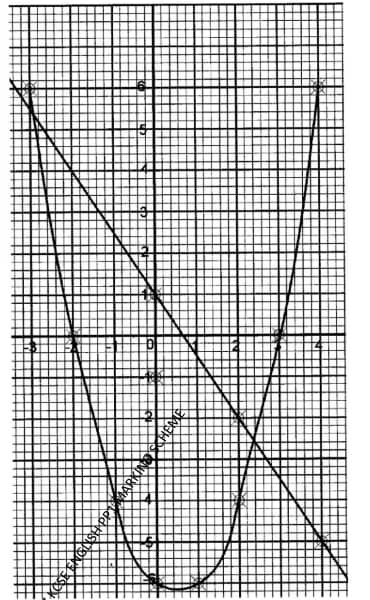
    3. Line y = ⁻³/₂x + 1
       x = 2.4
       x = − 2.8
19.  
    1. 50 000 x 0.9
       =Ksh 45000
    2.  
       1. 50 000 x 1.75
          =Ksh 87 500
       2. Amount to pay in instalments;
          = 87500 x 0.8
          =Ksh 70 000
          Monthly instalment
          = 70000
                28
          = Ksh 2 500
    3.  
       1. 50 000 x 1.04¹⁵
          = 90047.17528
          =Ksh 90047
       2. 90 047 − 50 000 = Ksh 40 047
20.  
    1. Length of CD
       CD² = 8² + 4.2² − 2 x 8 x 4.2 Cos 45°
       = 64 + 17.64 − 16 x 4.2 x 07071
       =81.64 − 47.52 = 34.12
       CD = √34.12 = 5.8
    2. Angle ABD:
       5.3² = 6² + 4.2² − 2 x 6 x 4.2 Cos θ
       Cos θ = 36+17.64 − 5.3²
                           50.4
       θ = Cos⁻¹ 0.5069
       θ = 59.5°
    3. Angle BCD:
       sin BCD = sin 45
          4.2           5.8
       Sin BCD = 4.2 x sin 45
                           5.8
       Angle BCD = sin⁻¹0.5120
                       = 30.8°
    4. Area of ΔABD:
       = ½ x 6 x 4.2 sin 59.5
       =10.9cm

21. Dr				Cr
    Date 2017	Particulars	Folio	Amount Ksh.	Date 2017	Particualrs	Folio	Amount Ksh.
    February 1	Balance b/f		10 000	February 3	Feeds		2 500
    13	Broilers		12 000	7	Water		750
    17	Eggs		4 000	11	Materials		1 900
    24	Chicks		5 000	21	Wages		3 500
    26	Layers		15 000	25	Electricity		1 300
    				28	Incubator		12 500
    				28	Balance c/d		23 550
    			46 000				46 000
    March 1	Balance b/f		23 550

22.  
    1. 
       

       Marks	1-10	11-20	21-30	31-40	41-50	51-60	61-70	71-80	81-90	91-100
       Frequency	2	4	5	8	11	9	5	3	2	1
       Cumulative frequency	2	6	11	19	30	39	44	47	49	50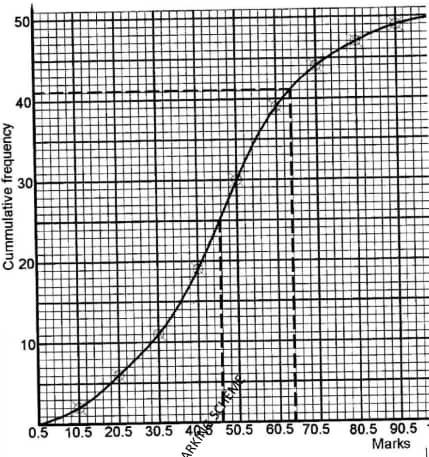

       
       
    2.  
       1. median = 46
       2. 50 − 41
          = 9
          % = ⁹/₅₀ × 100
              = 18%
23.  
    1. P(VV) = ⁵/₈ × ³/₇ 
               = ¹⁵/₅₆ 
       P(GG) = ³/₈ × ⁴/₇ 
                 = ¹²/₅₆ 
       P(same colour) = ¹⁵/₅₆ + ¹²/₅₆
                              ^{= 27}/₅₆ 
    2.  
       1. P(V_BV_B) = ⁵/₈ × ⁴/₇ 
                      = ⁵/₁₄ 
          P(V_CV_C) = ³/₇ × ²/₆ 
                       = ¹/₇
          ∴ p(V_BV_B) + P(V_CV_C)
          = ⁵/₁₄ + ¹/₇ = ½
       2. P(all violet)
          = ⁵/₁₄ × ¹/₇ 
          = ⁵/₉₈ 
24.  
    1.   
       
       Vetices: A'(4,4), B'(6,10), C'(10,6)
    2.  
       
       2a + 2b = −2
       5a + 3b = −5
       6a + 6b = −6
       10a + 6b = −10
       4a = −4
        a = −1
       2(⁻1) + 2b = ⁻2 ⇒ b = 0
       2c + 2d = 2
       5c + 3d = 3
       6c + 6d = 6 
       10c + 6d = 6
       4c = 0
        c = 0
       ∴ 0 + 2d = 2 ⇒ d − 1
        
    3.  
       
       vertices: A'''(⁻2, ⁻2), B'''(⁻5, ⁻7), C'''(⁻3, ⁻1)