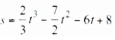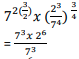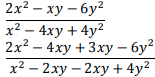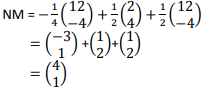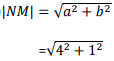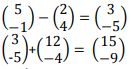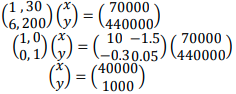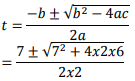Instructions to Candidates
- This paper consists of two sections; Section I and Section II.
- Answer all the questions in Section I and only five questions from Section II.
- Show all the steps in your calculations, giving your answers at each stage
- Marks may be given for correct working even if the answer is wrong.
- 8 Non-programmable silent electronic calculators and KNEC Mathematical tables may be used. except where stated otherwise.
- Candidates should answer the questions in English.
SECTION I (50 marks)
- Answer all the questions in this section in the spaces provided.
- Without using mathematical tables or a calculator, evaluate (3 marks)
−3(6+−2)−−12÷4+5
−4x−6+−3x5 - Express
as a mixed number. (3 marks)
- Without using a calculator or mathematical tables, evaluate: (3 marks)
- A rectangular floor of a room measures 5.4 m long and 4.2 m wide. The room is to be covered with square tiles. Calculate the minimum number of square tiles that can be used to cover the floor. (4 marks)
- Simplify
(3 marks)
- The line 2y+x= 1 is perpendicular to a line L. Line L passes through point (2,−1), Determine the equation of L in the form y = mx + c, where m and c are constants. (3 marks)
- The sum of the interior angles of a regular polygon is 12600. Find the size of each exterior angle of the polygon. (3 marks)
- Using the grid provided below, solve the simultaneous equations.
X−4y = −5 (3 marks)
−x+2y =1 - Given that sin(θ+30°)=cos2θ, find the value of cos(θ+40°).(3 marks)
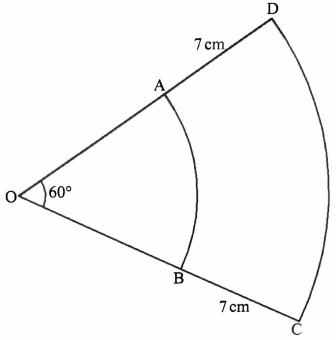
- In the figure below, AB and CD are arcs of two concentric circles, centre O. Angle AOB = 60° and AD=BC=7cm.
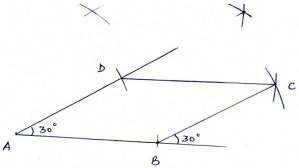
Given that the perimeter of ABCD is 28 2/3 cm, find OA, the radius of the inner circle. (3 marks) - Using a ruler and a pair of compasses only, construct a parallelogram ABCD in which AB = 6cm, BC = 5cm and angle ADC = 150°. (3 marks)
- A Kenyan Non-Governmental Organization (NGO) received a donation of 200 000 US dollars. The money was converted into Kenyan shillings in a bank which buys and sells foreign currency as follows:
Buying (Ksh) Selling (Ksh)
1 US Dollar 102.40 102.50
100 Japanese Yen 92.80 93.30- Calculate the amount of money, in Kenya Shillings, the NGO received. (1 mark )
- The NGO used 90% of the donation to buy a machine from Japan. Calculate the cost of the machine to the nearest Japanese Yen. (3 marks)
- A chord of a circle, 7 cm long subtends an angle of 60° at the centre of the circle. Determine the area correct to 2 decimal places, of the major segment of the circle. (4 marks)
- A vertical electric pole was erected 6.4m from the foot of a vertical fencing pole on the same horizontal level. The fencing pole is 2m high. The angle of elevation of the top of the electric pole from the top of the fencing pole is 30°. Determine the height of the electric pole correct to 1 decimal place. (2 marks)
- In a 4x400 m relay competition, a team of athletes each completed their round in 45 sec, 43 sec, 44 sec and 45 see respectively. If the race started at 1:35:31 p.m., find the time when the team completed the race.
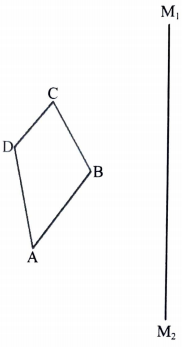
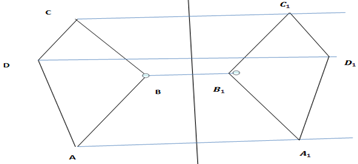
(3 marks) - The figure below shows a quadrilateral ABCD and a mirror line M1M2.
- Draw quadrilateral A'B'C'D', the image of ABCD, under a reflection in the mirror line M1M2. (2 marks)
- State the type of congruency between ABCD and A'B'C'D'. (1 mark)
SECTION II (50 marks)
- Answer any five questions from this section in the spaces provided.
- Three business partners, Kosgei, Kimani and Atieno contributed Ksh 1,750,000 towards an investment. Kosgei contributed 20% of the money. Kimani and Atieno contributed the remainder in the ratio 3:5 respectively.
-
- Calculate the amount of money Kimani contributed. (2 marks)
- Find the ratio of the contributions by the three partners. (2 marks)
- The money earned a compound interest at a rate of 8% per annum. After 3 years, the partners withdrew the interest and donated 10% to a charitable organisation. The partners then shared the remainder in the ratio of their contributions.
Calculate the amount of money, to the nearest shilling, that each partner received.
(6 marks)
-
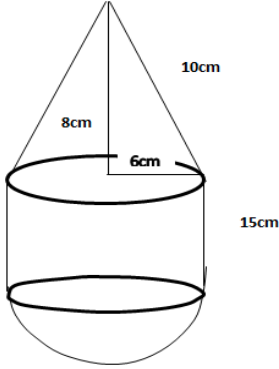
- A solid consists of a conical part, a cylindrical part and a hemispherical part. All the parts have the same diameter of 12cm. The height of the cylindrical part is 15cm and the slanting height of the conical part is 10 cm. (Take π = 3.142).
Calculate the:- height of the solid; (2 marks)
- surface area of the solid, correct to 1 decimal place,(4 marks)
- volume of the solid, correct to 1 decimal place. (4 marks)
- The average speed of a pick-up was 20km/h faster than the average speed of a lorry. The pick-up took 45 minutes less than the lorry to cover a distance of 180 km.
- If the speed of the lorry was x km/h:
- Write expressions in terms of x for the time taken by the lorry and the pick-up respectively to cover the distance of 180 km (2 marks)
- Determine the speed of the lorry and that of the pick-up. (5 marks)
- The distance between towns A and B is 240 km. On a certain day the pick-up started from town A at 8.30 a.m. and the lorry started from town B at the same time. Determine the time that the lorry and the pick-up met. (3 marks)
- If the speed of the lorry was x km/h:
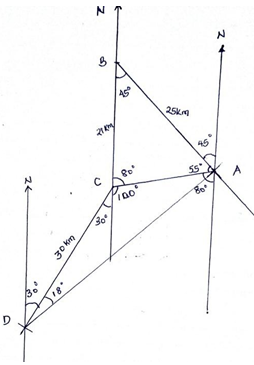
- A forest is enclosed by four straight boundaries AB, BC, CD and DA. Point B is 25km on a bearing of 315° from A, C is directly south of B on a bearing of 260° from A and D is 30km on a bearing of 210° from C.
- Using a scale of 1:500,000, represent the above information on a scale drawing
(3 marks) - Using the scale drawing, determine the:
- distance, in kilometres, of D from A: (2 marks)
- bearing of A from D (1 mark)
- Calculate the area, correct to 1 decimal place, of the forest in square kilometres.
(4 marks)
- Using a scale of 1:500,000, represent the above information on a scale drawing
- The position vectors of points A and B are OA=
and OB =
.A point M is on AB such that AM = ½AB and a point N is on OB such that ON:NB= 1:3.
- Find:
- AB (2 marks)
- NM; (3 marks)
- lNMl, correct to 1 decimal place. (2 marks)
- A translation vector maps A onto A'(5,−1). Find the coordinates of the image of B under the translation vector. (3 marks)
- Find:
- The number of students in 40 schools in a certain sub-county were recorded as follows:
238 100 173 115 398 597 572 299
255 750 587 403 250 217 797 386
362 486 453 279 436 248 780 316
529 305 372 286 842 235 420 492
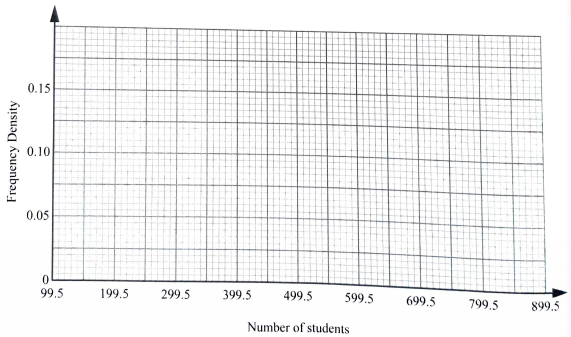
226 245 695 720 267 617 198 830- Complete the frequency distribution table below for the data. (2 marks)
Number of students 100-199 200-249 250-399 400-599 600-799 800-849 Number of schools - On the grid provided, draw a histogram to represent the data. (4 marks)
- Use the histogram to estimate the:
- median; (2 marks)
- number of schools with more than 350 students. (2 marks)
- Complete the frequency distribution table below for the data. (2 marks)
-
- Given that matrix M =
is a singular matrix, 23, find the value of p. (3 marks)
- Kirai earned a basic salary of Ksh x per month and Ksh y for each extra hour worked. Mutua's basic salary is 20% more than Kirai's basic salary but also earns Ksh y for each extra hour worked. In a certain month, Kirai worked 30 extra hours and earned a total of Ksh 70,000 while Mutua worked an extra 40 hours and earned a total of Ksh 88,000.
- Form two equations in x and y to represent Kirai's and Mutua's total earnings. () (2 marks)
- Use matrix method to solve for x and y. (5 marks)
- Given that matrix M =
- The displacement, s metres, of a moving particle after t seconds is given by
Determine the:- velocity of the particle when t = 5: (3 marks)
- time, t seconds, when the particle is momentarily at rest; (3 marks)
- displacement, s metres, when the particle is momentarily at rest; (2 marks)
- acceleration of the particle when t = 4 seconds. (2 marks)

Marking Scheme
- −3(6+−2)−−12÷4+5
−4x−6+−3x5
−3(4) + 3 + 5
24 +−15
=−4
9
9r = 50
r= 55/9
=26
=64- 42 =2×3×7
54 =2×33
G.C.D =2×3=6
∴ G.C.D of 5.4 and 4.2=0.6
No of tiles = area room
area tile
= 5.4 × 4.2
0.6×0.6
=63 tiles -
= (2x + 3y)
(x − 2y) - m1= −½
m2 = 2 (2,−1)
y=m(x −x value) + y value
y=2(x − 2)−1
y=2x−5 - (n−2)180=1260
n=9 sides
Ext ∠ = 360
9
=40° - X−4y = −5
−x+2y =1
X−4y = −5
x −5 3 y 0 2
−x+2y =1
x −1 7 y 0 4
x=3 and y=2 - sin(θ+30°)=cos2θ
θ+30+2θ=90
∴ cos 60=0.5 - θ=60°=π/3radians
Arc length =θr where θ is in radians
π/3 × r + π/3×(r+7) +7+7 =282/3
2π/3r =142/3− 7π/3
r=3.502 -
-
- 1dollar=Ksh 102.40
200000dollars =?
200000dollars × Ksh102.40
1dollar
= Ksh 20,480,000 - 100 Jap yen= Ksh 93.30
? = 0.9(20,480,000)
=0.9(20480000) × 100yen
93.3
=19755627.01
≈19,755,627
- 1dollar=Ksh 102.40
- θ =π/3 θ=360−60=300
θ =2π−π/3 arc length, b = θ/360 . 2πr
=12/3π chord= radius = 7cm
area=½θr2 b = 300 × 2 × 22 × 7
where θ is in radians 360 7
=½ × 5/3π × 7 × 7 =362/3cm
=128.28cm2 area=½b.r
=½ × 362/3 × 7
=1281/3cm2
≈128.33cm2 - 2 + 6.4 tan 30
= 5.695
≈ 5.7m - ℎr min s
1 35 31
0 0 45
0 0 43
0 0 44
+0 0 45
1 38 28
= 1:38:28pm -
- Indirect congruent or opposite congruency
-
-
- Ko : Ki : At
0.2: 0.3: 0.5
Ki = 30 % of 1750000
=Ksh. 525000 - 2:3:5
- Ko : Ki : At
- A =PRnwhere R = 1+r
=1750000(1.083)
=2204496
Shared amount=90% × 2204496
=1984046.4
Kosgei=0.2 ×1984046.4
=Ksh. 396809
Kimani=0.3 ×1984046.4
=Ksh. 595214
Atieno=0.5 x1984046.4
=Ksh. 992023
-
-
-
Total height =8+15+6
=29 cm - SA= πrl + 2πr2 + 2πrh
= 3.142× 6×10 + 2×3.142×62 + 2×3.142×6×15
=188.52+565.56+226.224
= 980.304
≈ 980.3 sq.cm - V=1/3xAh + πr2h + 2/3πr3
= 1/3 × 3.142×36×8 + 3.142×36×15 + 2/3 × 3.142 × 216
=2450.76 cubic cm
≈2450.8cm3
-
-
-
- lorry time = 180km hrs
x
Pick up time=180km hrs
x+20 - 180km − 180km = 3
x x+20 4
x2 + 20x − 4800= 0
(x − 60)(x + 80) = 0
x = 60km/h or −80km/h
∴ x = 60km/h
hence lorry = 60km/h &
pick up = 80km/h
- lorry time = 180km hrs
- distance pick up +distance lorry = 240km
80(t − 8.30am) + 60 (t − 8. 30am) = 240
where t meeting time
140 t− 680 − 510 = 240
t ≈ 1013hrs
-
-
-
-
- AD=8.7cm × 5km
1cm
= 43.5km ± 0.5 - bearing of A from D is 048° or N48°E
- AD=8.7cm × 5km
- A∆ABC =½ × 21 × 25 sin 45°
= 185.62 km2
A∆ACD = ½ ×30 × 43.5 sin 18°
=201.63km2
total area= 185.62 + 201.63
= 387.25km2
≈ 387.3km2
-
-
- AB= (−2) + (12 ) = (10 )
(−4) (−4) ( −8)
=√17
=4.123
≈4.1
- AB= (−2) + (12 ) = (10 )
- T=A−1−A
∴ B1(15,−9)
-
-
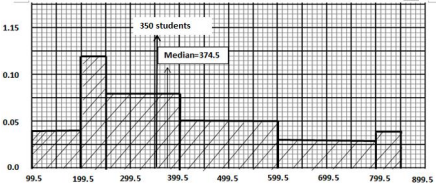
class tally f fd cf 100-199 llll 4 0.04 4 200-249 llll l 6 0.12 10 250-399 llll llll ll 12 0.08 22 400-599 llll llll 10 0.05 32 600-799 llll l 6 0.03 38 800-849 ll 2 0.04 40 -
- Median psn=40/2 =20th value
=10 + x × 0.08 = 20
x = 125
Median = 125+249.5
=374.5 - 49.5 × 0.08 + 10 + 6 + 2
= 21.96
≈ 22 schools
- Median psn=40/2 =20th value
-
-
- 3 −{p (p − ½)} = 0
3 − p2 + ½p = 0
2p2 − p − 6 = 0
(p − 2)(2p + 3) = 0
p = 2 or − 1.5 -
- Kirai x + 30y = 70000 … (i)
Mutua 1.2x + 40y = 88000 … (ii)
6x + 200y = 440000…(ii)
∴ x = 40000 and y = 1000
- Kirai x + 30y = 70000 … (i)
- 3 −{p (p − ½)} = 0
-
- V=2t2 − 7t − 6 iƒ t = 5
=2t2−7t−6
=9 m/s - V=2t2−7t−6 =0
=4.212 s or -0.7122 s
∴ t = 4.212s - S= 2/3t3 − 7/2t2 − 6t + 8 iƒ t = 4.212
S= 2/3t3 − 7/2t2 − 6t + 8
=−37.5487m - a = dv/dt = 4t − 7 iƒ t = 4
=4 x 4 − 7
=9m/s2
- V=2t2 − 7t − 6 iƒ t = 5
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - KCSE 2020 Past Papers.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students