SECTION I (50 Marks)
Answer all questions in this section
- When asked to find 7/18 of a certain number, Juma found by mistake 7/8 of it. Hence the answer was too large by 105. Find the number. (3 marks)
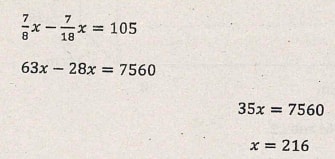
- Simplify leaving the answer in the form of a√2 + b√5 where a and b are constants. (3 marks)
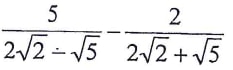
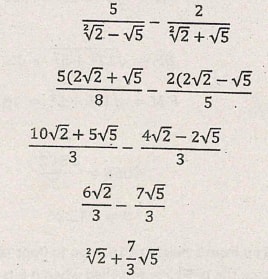
-
- Expand completely (x-0.2)5 (1 mark)
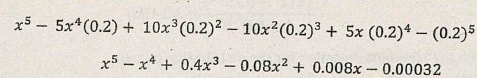
- Hence use your expansion to find the exact value of (9.8)5 (2 marks)

- Expand completely (x-0.2)5 (1 mark)
- The figure below represents a solid cuboid ABCDEFGH with a rectangular base. AB = 12 cm, BC = 10 cm and CH = 5 cm. M is the midpoint of GH
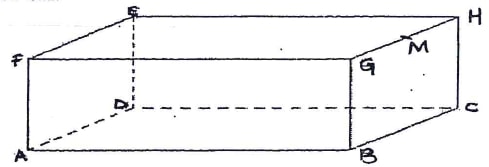
Calculate the anle between BM and CE (3 marks)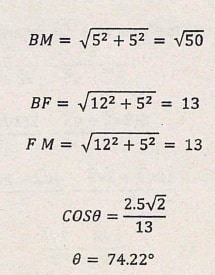
- A ball allowed to drop from a height of 16 cm on to a flor rebounds to 3/4 of its previous height. Find the total distance the ball wil have travelled when it hits the ground for the tenth time correct to four significant figures. (2 marks)
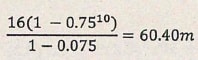
- Calculate the standard deviation for the distribution below (4 marks)
No. of children 0 1 2 3 4 5 6 No. of families 4 2 4 7 8 3 2 Fx 0 2 8 21 32 15 12 Fx2 0 2 16 63 128 75 72 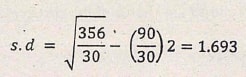
- Make x the subject of the formula (3 marks)
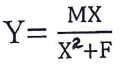
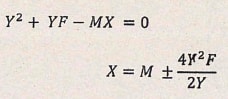
- A triangle whose area is 7.2 cm2 is mapped onto a triangle whose area is 3.6cm2 by the matrix given below. Find the two possible values of x. (3 marks)
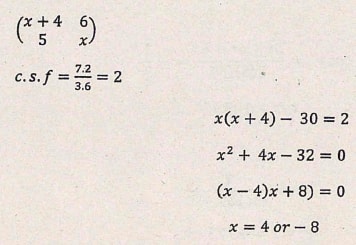
- Simplify completely the expression (3 marks)
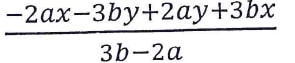
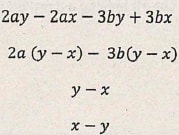
- Find the amount after 3.25 years if Kshs 234,000 is invested at 10% p.a compunded semi annually. (3 marks)
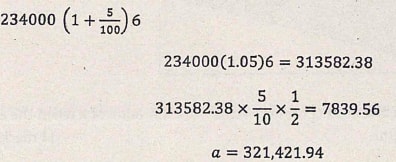
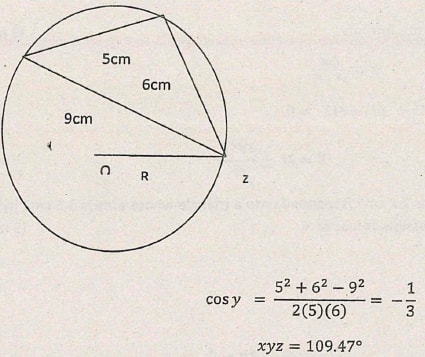
- In the figure below XY and YZ are chords of the circle centre O. XY = 6 cm and XZ = 9 cm. Find
- The value of angle XYZ
- The length of OZ
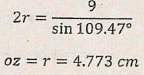
- The value of angle XYZ
- In the figure below PQRS is a rectangle. PQ = 30cm and PS = 10 cm
The unshaded portions are cut off leaving a parallelogram ABCD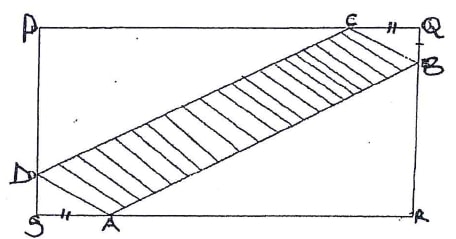
Given that line BQ = DS = x cm and line CQ = SA = 3x cm. Find the value of x when the area of the parallelogram ABCD is maximum (4 marks)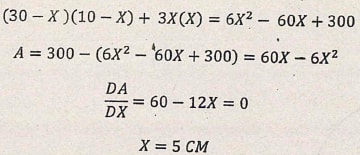
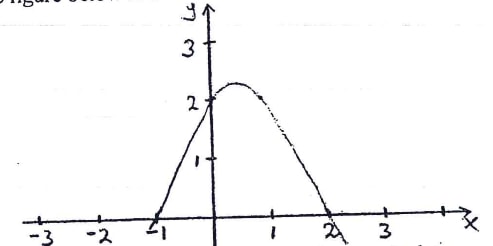
- The figure below is a sketch of the graph of the quadratic function D = k(x-2) (x+1). Find the value of k. (3 marks)
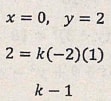
- Evaluate without using mathematical tables or calculator (2 marks)
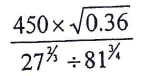
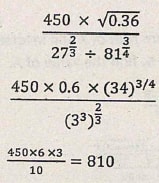
- The figure below shows a circle passing through the origin cutting through P (K,0) and Q (0,K). If its radius is 3√2, find the equation of the circle in the form of x2 + y2 +ax + by + c = 0 (4 marks)
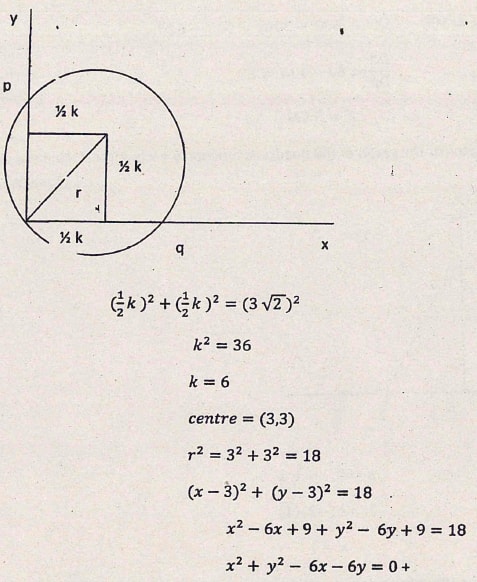
- A quantity Q varies jointly as the square root of X and inversely as Y. Given that when Y is reduced by 20% and X increased by A%, Q increased by 37.55 %, find the value of A. (3 marks)
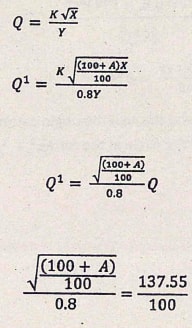
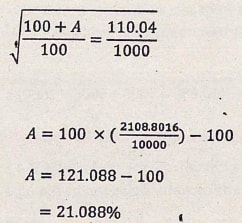
SECTION II (50 Marks)
Answer any Five Questions from this Section
- The table below shows income tax rate for the year 2014
Income in Kshs per month Rate % 1 - 9680 10% 9681 - 18800 15% 18801 - 27920 20% 27921 - 37920 25% Over 37920 30% - In the tax year of 2014 the tax of Kamau's monthly income was Ksh 10,880. If he is entitled to a tax relief of Ksh 1156. Find
- Gross tax of Kamau (1 mark)
10880 + 1156 = 12036 - Taxable income per month in shillings (5 marks)
- 9680 × 0.1 = 968
9120 × 0.15 = 1368
9120 × 0.2 = 1824
1000 × 0.25 = 2500
17920 × 0.3 = 5376
Taxable = 55840
5376/0.3 = 17920
- 9680 × 0.1 = 968
- Gross tax of Kamau (1 mark)
- Apart from basic salary, Mr. Kamau also earns a house allowance of Ksh 12, 000, a medicall allowance of Ksh 3,060 and a hardship allowance of Ksh 4,635. Find the his basic salary per month (2 marks)
- 55840 − (12,000 + 3060 + 4635) = 36145
- Other deductions for Kamau include; SACCO loan kshs. 3000, SACCO contributions Ksh. 6,000 and hire purchase repayment Kshs. 2,000. Calculate Kamau's net pay per month (2 marks)
- 55840 − (10880 + 3000 + 6000+ 2000) = 33960
- In the tax year of 2014 the tax of Kamau's monthly income was Ksh 10,880. If he is entitled to a tax relief of Ksh 1156. Find
- Water flows through a cylindrical pipe of diameter 8.4 cm at a speed of 50m/minute.
- Calculate the volume of water delivered by the pipe per minute in litres. (π=22/7) (3 marks)
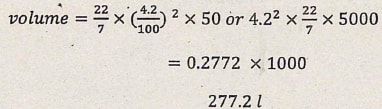
- A cylindrical storage tank of radius 105 cm is filled by water from this pipe at the same rate of flow. Water begins flowing into the empty storage tank at 9.30 a.m and is full at 2.00 pm. Calculate the height of the tank in metres. (4 marks)
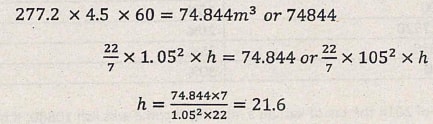
- A family consumes the capacity of this tank in one month. The cost of water is sh 50 per thousand litres and fixed basic charge of Ksh 1650 per month. Calculate the cost of this family's water bill for a year. (3 mks)
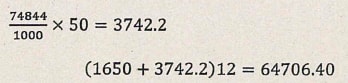
- Calculate the volume of water delivered by the pipe per minute in litres. (π=22/7) (3 marks)
- The position of two towns A and b on earth's surface are (60oN, 36oE) and (60oN, 144oW) respectively. Taking the radius of the earth as 6370 km and π =22/7
- Calculate the shortest distance between A and B in km to 1 dp. (2 marks)
- 60/360 × 22/7 × 6370 = 3336.7 km
- Calculate the distance between A and B along the parallel of latitudes in km (2 marks)
- 1/2 × 22/7 × 6370 cos 60 = 5005 km
- Another town C is 840 km east of twon B and on the same latitude as town A and B. Find the position of town C. (3 marks)
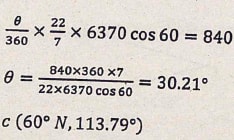
- If an aircraft leaves town A at 8.30 am at a speed of 720 km/h to K (60oN,50oW). At what local time is it expected at K to the nearest minute? (3 marks)
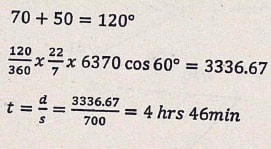
- Calculate the shortest distance between A and B in km to 1 dp. (2 marks)
-
- In a chemistry form 4 class in Jaribu high school 1/3 of the class are girls and the rest are boys. 4/5 of the boys and 9/10 of the girls are right handed while the rest are left handed. The probability that a right handed student breaks a conical flask in any practical session is 3/10 and the corresponding probability for a left handed student is 4/10.
- Represnt the above infomation on a tree diagram (2 marks)
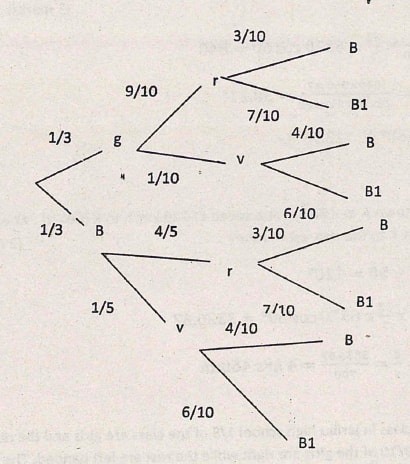
- Determine the probability that a student chosen at random from the class is left handed and does not break a conical flask in its simplest form (2 marks)
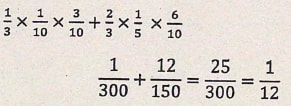
- Determine the probability that the flask is broken in any practical session in simplest form (2 marks)
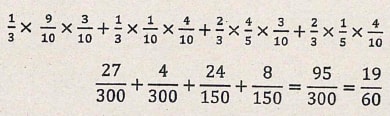
- Represnt the above infomation on a tree diagram (2 marks)
- The probability of Peter scoring grade A in his exam is 0.6 while the probability of Ali scoring the same grade is 0.7.
Determine the probability that,- Both will score grade A (1 mark)
- 0.6 × 0.7 = 0.42
- None of them will score grade A (1 mark)
- 0.4 × 0.3 = 0.12
- Only one of them will score grade A (1 mark)
- 0.6 × 0.3 + 0.4 × 0.7 = 0.46
- At least one of them will score grade A (1 mark)
- 1p(none) = 1 − 0.12 = 0.88
- Both will score grade A (1 mark)
- In a chemistry form 4 class in Jaribu high school 1/3 of the class are girls and the rest are boys. 4/5 of the boys and 9/10 of the girls are right handed while the rest are left handed. The probability that a right handed student breaks a conical flask in any practical session is 3/10 and the corresponding probability for a left handed student is 4/10.
- In the figfure below, O is the centre of the cricle. PQR is a tangent to the circle at Q. Angle PQS = 28o, angle UTQ = 54o and UT = TQ
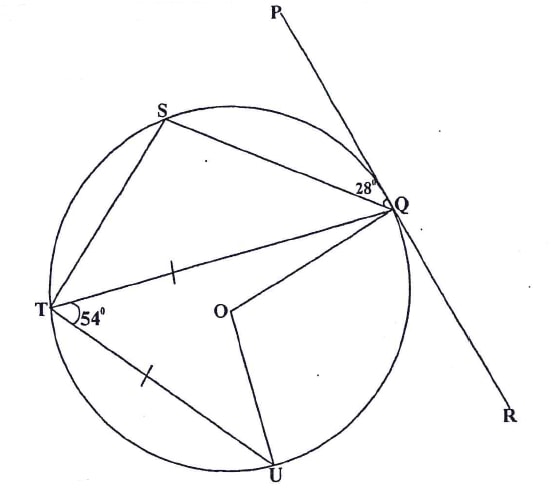
Giving reasons, detrmine the size of- Angle STQ (2 marks)
- 28o Angles in alternate segments
- Angle TQU (2 marks)
- (180 − 54)/2 = 65o Base angles of an isosceles triangle
- Angle TQS (2 marks)
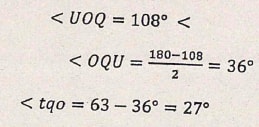

- Reflex angle UOQ (2 marks)
- 360 − 108 = 282o angles at a point
- Angle TQR (2 marks)
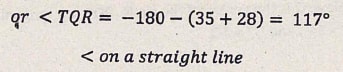
- Angle STQ (2 marks)
-
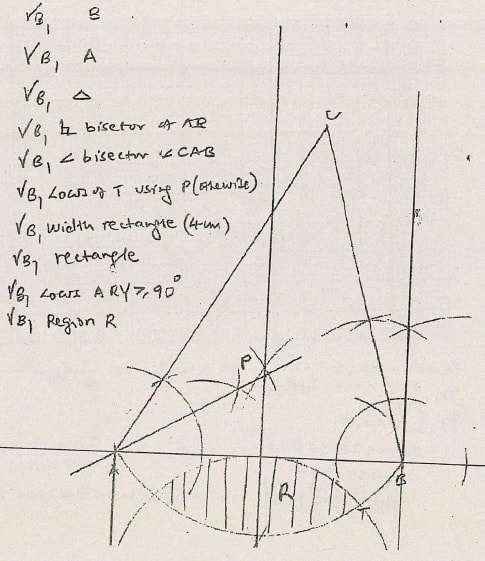
- Using a ruler and pair of compasses only, construct a triangle ABC such that AB = 8 cm and angle ABC = 75o and angle BCA = 45o. Let AB be on the line drawn below(3 marks)
- On the upper side of line AB, Locate the locus of p such that AP = PB and P is equidistant from AC and AB. (2 marks)
- Construct the locus of a point T such that angle ATB = 120o (2 marks)
- Construct a rectanbgle ABXY on the lower side of AB such that its area is 32 cm2 (2 marks)
- Shade the region R inside the rectangle suchthat XRY≥90o and angle ATB≥120o (1 mark)
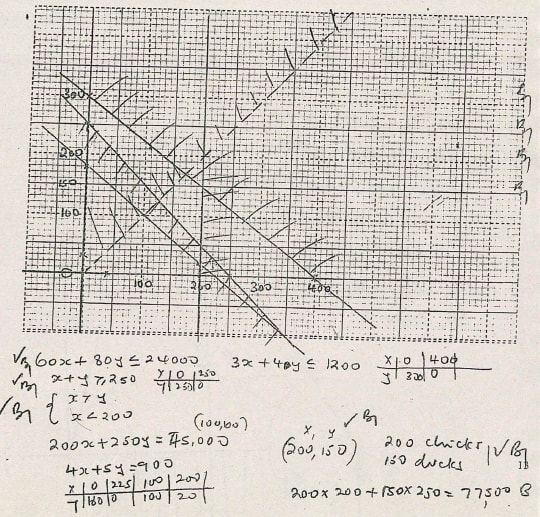
- A farmer wishes to keep some chicks and ducks. Chicks cost Kshs. 60 each while ducks costs Kshs. 80 each. She cannot afford to spend more than Ksh 24,000. She finds it uneconomical to keep less than 250 birds. She also wishes to keep more chicks than ducks but chicks must be less than 200.
- Taking x and y to be the number of chicks and ducks resectively, write down all the inequalities that satisfy the above conditions (3 marks)
- Represent the inequalities graphically using a sclae of 1 cm represents 50 birds on both axis (4 marks)
- If the farmer sells a mature chick at Kshs. 200 and a duck at Kshs 250, find the number of chicks and ducks she must keep in order to maximize her revenue. State the maximum revenue (3 marks)
- The diagram below shows a line PQ and the curve y = 2x − x2 intesrecting at point P and Q
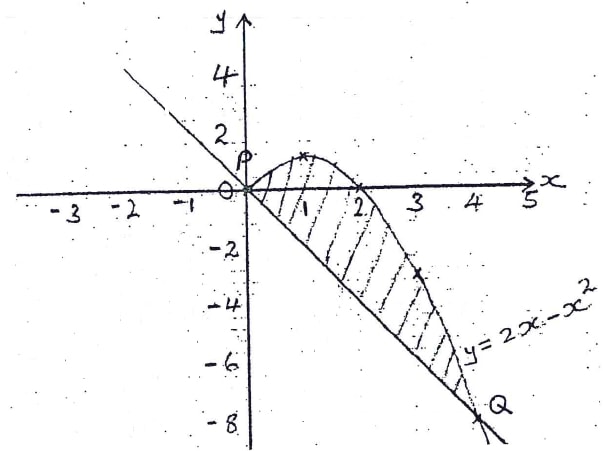
- Find the coordinates of P and Q
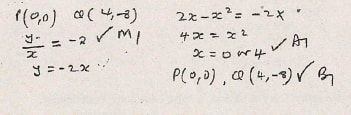
- Calculate the area of the shaded region
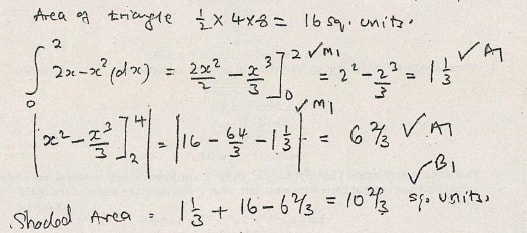
- Find the coordinates of P and Q
Download MATHEMATICS PAPER 2 Marking Scheme - 2019 KCSE Prediction Answers Set 1.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

