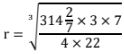MATHEMATICS
PAPER 1
Instructions to Candidates
- This paper consists of two sections; Section I and Section II.
- Answer all the questions in Section I and any five questions from Section II
- Show all the steps in your calculations, giving your answers at each stage in the spaces provided below each question
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.

Questions
Section I (50 Marks)
Answer ALL questions in the section in the space provided:
- Calculate the total value of digit 6 in the number 435.609 hence state it in words. (2 marks)
- In a covid-19 vaccination centre, teachers may receive their jabs from either of the two doctors stationed at the two tents. On an average, one doctor takes 2 minutes while the other doctor takes 3 minutes to serve one teacher. If the two doctors start to serve the teachers at the same time, find the shortest time it takes to vaccinate a total of 300 teachers. (3 marks)
- Evaluate (3 marks)
2½ of 1¾ - 5¼
1²/₅ + 2(1¼ - 2¾) - Given that ²/₃x = ½ and ¾y = ³/₂ calculate the value . (3 marks)
x+y
xy - A car dealer charges 10% commission for selling a car. If he received a commission of Ksh.27,500 for selling a Toyota Mark X, calculate the amount of money that the owner received from the sale of his car if the dealer added an extra charges of 5 %. (3 marks)
- Find all the integral values of x which satisfy the inequality (3 marks)
3 (1 + x) < 5x – 14 < x + 46 - Use Table of logarithms to evaluate (4 marks)
- Calculate the value of p given that sin(3p − 20)° − cos(p + 30)° = 0. (2 marks)
- A rhombic cardboard whose diagonals are of lengths 16cm and 12cm is to be surrounded by a golden chain. Calculate the length of the chain enough to surround it just once. (3 marks)
- Solve for c in the equation(3 marks)
2+2ᶜ ‾⁴ = 26.
5 - Find the value of k given that 2k − 1 is the mean of 3k + 2 and 4k + 1. (3 marks)
- The co-ordinates of P and Q are (6, 5) and (2, 3) respectively. Find to one decimal place magnitude of 2PQ. (3 marks)
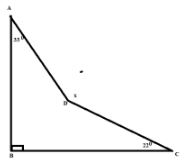
- The figure below shows quadrilateral ABCD in which angle ABC=90°, BAD=33° and BCD=22 ° .
Calculate the size of the obtuse angle ADC=x. (3 marks) - A group of x Form 4 students decided to contribute equally to raise a total of sh. 810 to buy a birthday cake for the School President. Three of the x students were sent home for fees before submitting their contribution. As a result, each of the remaining students had to contribute an extra of sh. 9 to realize the same amount. Form an equation in x and hence find the number of students who actually contributed towards the birthday cake. (4 marks)
- A measuring cylinder of base radius 5cm contains water whose level reads 6cm high. A spherical object is immersed in the water and the new level reads 10cm. Calculate the radius of the spherical object. (4 marks)
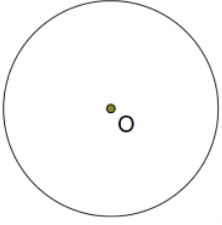
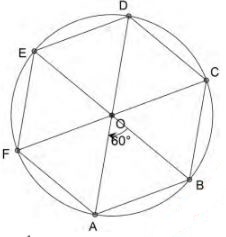
- The figure below shows a circle of centre O. The vertices of a regular hexagon ABCDEF lies directly on its circumference.
Construct the hexagon ABCDEF hence calculate the area of the hexagon. (4 marks)
Section II (50 Marks)
Answer ONLY FIVE questions in the section in the space provided:
- In a certain meeting, there were 95 men in attendance. Fifty more women than men and twice as many children as men also attended.
- Determine the number of people in meeting. (2 marks)
- Find the percentage of children in attendance, correct to three significant figures. (2 marks)
- A hall for the meeting was fitted with benches that could accommodate either 10 children or 7 adults per bench. Find the number of benches:
- used by the children. (2 marks)
- completely filled by the adults. (2 marks)
- adults who would fill the unoccupied space. (2 marks)
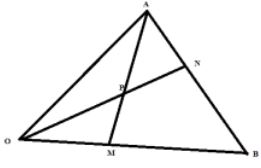
- The figure below shows triangle OAB in which OA =a and OB=b. M and N are points on OB and AB respectively such that OM=1/3OB and 5AN=2AB. Lines AM and ON meets at P such that OP =5/9ON.
- Express the following vectors in terms of a and b
___- AB (1 mark)
___ - ON (2 marks)
___ - AM (1 mark)
__ ___
- AB (1 mark)
- Express AP and PM in terms of a and b and hence show the points A, P and M are collinear. (5 marks)
- State the ratio AP: PM. (1 mark)
- Express the following vectors in terms of a and b
- A particle moving along a straight line covers a distance of 5 meters in time t seconds from a fixed point O on the line where S= t3 - 6t2 + 8t – 4.
Find;- the velocity of the particle when t=5. (3 marks)
- the acceleration where t=5 seconds. (2 marks)
- the time when the velocity of the particle is constant. (2 marks)
- the time when the particle will be momentarily at rest. (3 marks)
- Four towns A,B,C and D are such that B is on a bearing of 247° and 6km from A. C is due SE and 4.8km from B. D is to the south of A and the bearing of C from D is S44°W
- Make a scale drawing showing the relative positions of A,B, C and D using the scale 1cm represents 1 kilometre. (4 marks)
- Use your drawing to determine
- The bearing of A from C. (1 mark
- The distance between C and D (1 mark)
- How far D is east of B (1 mark)
- The average speed of a cyclist from C to A if he takes 30 minutes between A and D and 20 minutes between D and A. (3 marks)
- A line L1 whose equation is 6x+2y+5k=0 passes through the point (-3,-1) and is perpendicular to L2 whose equation is 2px+9y=10. Find:
- the values of k and p. (4 marks)
- the equation of line L3 which is parallel to L2 in the form ax+by=c. (3 marks)
- the obtuse angle with which line L2 makes with x axis. (3 marks)
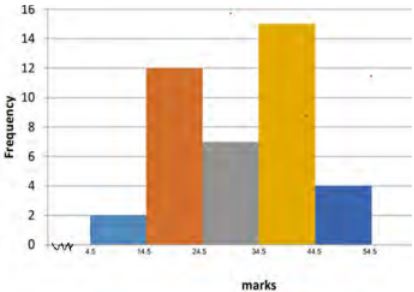
- The table shows the marks obtained by 40 candidates in an examination
marks 5 – 14 15 – 24 25 – 34 35– 44 45 – 54 Frequency 2 12 7 15 x - Calculate the value of x. (2 marks)
- Estimate the median mark. (3 marks)
- On the grid provided below draw a histogram to represent the data. (3 marks)
- If the pass mark was 40 marks and above, use the histogram to get the number of students that passed. (2 marks)
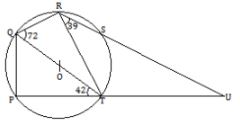
- In the figure below, QOT is a diameter, ∠QTP=42°, ∠TQR = 72° and ∠SRT =39°: RSU and PTU are straight lines.
Calculate the following, giving reasons:- ∠RST (2 marks)
- ∠SUT (2 marks)
- ∠PST(2 marks)
- Obtuse ∠ROT (2 marks)
- ∠SQT (2 marks)
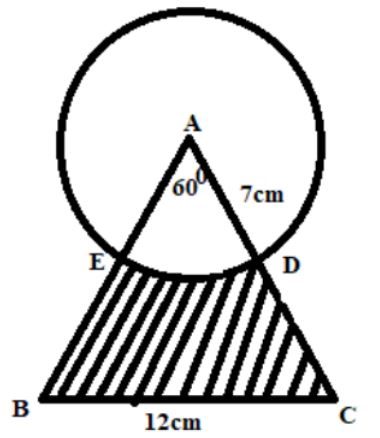
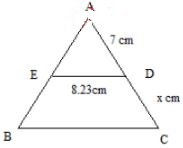
- The figure below shows a cross sectional area of an emblem made of circular ring of centre A and radius AD=7cm adorned with an extension of an isosceles triangular plinth ABC whose base BC=12cm.
Calculate to 2 decimal places:- The length of the chord ED. (2 marks)
- The area of the shaded region. (4 marks)
- If the shaded region is made up of a different metal of density 1025kgm-3and the emblem is 2.5cm wide, calculate the mass, in grammes, of that kind of metal required for making 100 such emblems. (4 marks)

Marking Scheme
- 6 × 0.1 = 0.6 or 6/10
Six tenths - LCM=2 × 3 = 6
Doctor A will give jabs to 3 teachers in 6 minutes
Doctor B will give jabs to 2 teachers in 6 minutes
Both doctors will give jabs to 5 teachers in 6 minutes
Shortest time =300/5× 6
=6 hrs or 360 mins - Numerator
21/2 of 13/4− 51/4
=35/8− 51/4
=−7/8
Denominator
12/5 + 2 (−3/2)
=12/5− 3
=−8/5
∴−7/8×−5/8
=35/64 - 2/3x =1/2
x =1/2 × 3/2 = 3/4
3/4y =3/2
y=2
³/₄+ 2
2 × ³/₄
=11/4 × 2/3
= 15/6 =11/6 - If 10% = 27500
∴ 100% =100 × 27500
10
= 275000
Amount received =85 × 275000
= 233750 - 3 + 3x < 5x − 14
8.5 < x
5x − 14 < x + 46
x < 15
8.5 < x < 15
x = {9,10,11,12,13, 14} -
Number Std form Logs 0.921
0.00739
0.023
0.66649.21 x10-1
7.39 x 10-3
2.3 x 10-2
6.664 x 10-11.9643
3.8686+
3.8329
2.3617
1.4712
3
1.8237 - (3p − 20)° + (p + 30)° = 90°
p = 20° - l = √82 + 62
=10
P= 4 × 10
= 40 - 2 + 2c−4 = 130
2c−4 = 128
2c−4 = 27
c − 4 = 7
c = 11 - 3k + 2 + 4k + 1 = 2k − 1
2
7k + 3 = 4k − 2
3k = −5
k = −12/3 -
- < ADC + 90° + 22° + 33° = 360°
< ADC = 215°
< X = 360° − 215°
= 145° - 810 − 810 = 9
x − 3x
9x2 − 27x − 2430 = 0
x =3 ± 33
2
x = 18 or − 15
∴ x = 18
Hence number of students who paid were 15 - Volume of the sphere=22/7× 52 × 4 = 3142/7
4/3 ×22/7× r3 = 3142/7
r = 4.2cm
6 ×1/2× 32Sin 60° =23.3826859021798 cm2-
- 95 + 95 + 50 + 95 × 2 = 430
- % of children=190/430× 100%
= 44.2% -
- Number of benches occupied by children
=190/10
= 19 - Number of benches filled by adults
=240/7
=34.2857142857
=34 benches - 7-(240-34x7)
=5
- Number of benches occupied by children
-
-
- AB=AO+0B
=b - a - ON=OA+AN
= a + 2/5(b − a)
=3/5a + 2/5b - AM= AO+OM
= -a + 1/3b
- AB=AO+0B
- AP=AO+OP
=-a + 5/9(3/5a + 2/5b )
= -a+(1/3a + 2/9b )
=−2/3a + 2/9b
PM=PO+OM
=− (1/3a +2/9b )+1/3b
=−1/3a + 1/9b
AP=2PM hence is parallel to PM Since is parallel to has a common point P then the points A, P and M are collinear - AP:PM=2:1
-
-
- v = 3t2 − 12t + 8
v(5) = 3(5)2 − 12(5) + 8
= 23ms−1 - a = 6t − 12
a(5) = 6(5) − 12
= 18ms−2 - At constant velocity a = 0
6t − 12 = 0
t = 2s - At rest v = 0
3t2 − 12t + 8 = 0
t =12 ± 6.92820323027557
6
= 3.15 or 0.85s
- v = 3t2 − 12t + 8
-
- Scale diagram
-
- 020° or N20°
- 2.6 ± 0.1
- 5.5 ± 0.1
- speed
= 3.6+2.6
50/60
=7.4km/h
-
- 6(−3) + 2(−1) + 5k = 0
k = 4
6x + 2y + 20 = 0
y = −3x − 10
m1 = −3
m2 =1/3
2px + 9y = 10
y = −2/9px +10/9
−2/9p =1/3
p = −11/2 - y+2 = 1/3
x−3
3y + 6 = x − 3
x − 3y = 9 - tan∅ =1/3
∅ = 18.434948822922°
the obtuse angle = 180° − 18.434948822922°
= 161.6°
- 6(−3) + 2(−1) + 5k = 0
-
- x = 40 − (2 + 12 + 7 + 15)
x = 4 - 40/2= 20
Median = 24.5 + (20 − 14/7)10
= 331/14 -
- 4 + 4.5/10× 15
= 10.75
= 10 students
- x = 40 − (2 + 12 + 7 + 15)
-
- < RST =12(360° − (180° − 36°)) = 108°
Reason: The reflex angle subtended by the same chord on to the centre of the circle is always twice the angle subtended by the same chord in the minor segment - < SUT = 180° − 72° − (180° − (42° + 18° + 43°)) = 21°
Reason: Sum of interior angles of a triangle is 180° - < PST =< PQT = 90° − 42° = 48°
Reason: Angles subtended by the same chord, PT, on similar segment are equal. - Obtuse < ROT = 180° − 2(90° − 72°) = 144°
Reason: Angles on a straight line add up to 180° - < SQT = 39°
Reason: Angles subtended by the same chord, TS, on similar segment are equal.
- < RST =12(360° − (180° − 36°)) = 108°
-
-
sin 36° = ½ED
7
ED = 8.23cm -
x+7 = 12
7 8.23
x = 3.20656136087485
Area of ∆ABC =½ × 3.206561360874852 × sin72°
= 10.206561366087485
Area of the shaded part
=½ × 10.2065613660874852 sin 72° − 72 x 22/7× 72
360°
= 18.74 cm2 - Volume of one emblem = 2.5 × 18.74 = 46.85cm2
Volume of 100 emblems = 100 × 46.85 = 4685
Mass = 1.025 × 4685
= 4802.125
= 4802.13g
-
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - KCSE Prediction Papers 2023.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students