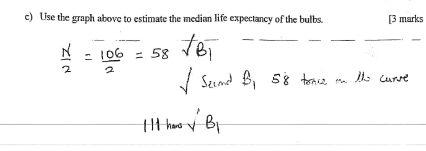- Calculate the percentage error in estimating 5.72 as 5.72. (3 marks)
- If
,
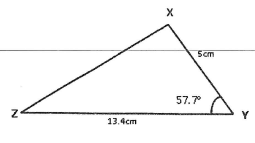
where k and x are rational numbers, find the value of k and x. - In triangle XYZ below, YZ = 13.4cm, XY = 5cm and <XYZ = 57.7o. Calculate the radius, to two decimal places, of the circumscribing circle to the triangle. (3 marks)
- The cash price of a bed is Kshs. 6500. Wambui bought it on hire purchase by making a down payment of Kshs. 2300 followed by 12 monthly instalments of Kshs. 490. Calculate the rate of the carrying charge to two decimal places if it is compounded. (4 marks)
- Using the substitution k = (m-3) solve for m in the equation 2(m-3)2 - 5 (m - 3) - 7 = 0 by completing square method. (4 marks)
- Simplify completely. (2 marks)
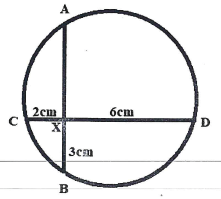
- In the figure below chord AB is perpendicular to chord CD at X and CX = 2cm, DX = 6cm and BX = 3cm.
Calculate the radius of the circle to two decimal places. (3 marks) - Expand and simplify (1 - 2x)6 in ascending powers of x up to the term in x3 then use the expansion to evaluate (1.02)6 to 4 decimal places. (3 marks)
- Determine the matrix T given that AT=B when
(3 marks)
- Find the coordinate of the centre and the radius of a circle whose equation is given as 3x2 + 3y2 - 12x + 18y + 8 = 0 (3 marks)
- A merchant blends 350kg of Kakuzi tea costing Sh 84 per kg with 140kg of KETEPA tea costing Sh 105 per kg. Calculate the price at which he must sell 1kg of the mixture to attain 15% profit. (3 marks)
- Kiptoo earns a monthly basic salary of Kshs. 25000. He is entitled to a tax relief of Kshs. 480 per month, a house and medical allowances of Kshs. 12000 and Kshs. 3000 respectively. Calculate his annual taxable income in Kenyan Pounds. (3 marks)
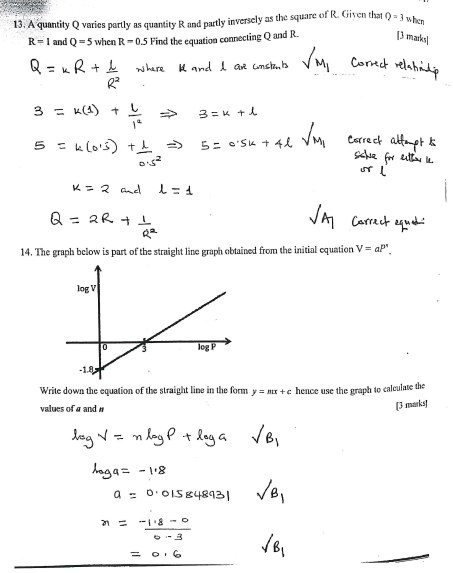
- A quantity Q varies partly as quantity R and partly inversely as the square of R. Given that Q = 3 when R = 1 and Q = 5 when R = 0.5, find the equation connecting Q and R. (3 marks)
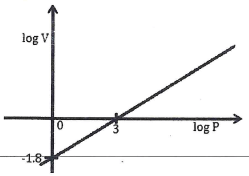
- The graph below is part of the straight line graph obtained from the initial equation V = aPn.
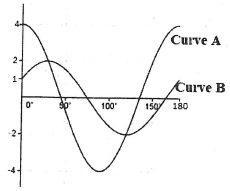
Write down the equation of the straight line in the form y = mx + c hence use the graph to calculate the values of a and n - The graph below shows two curves A and B drawn on the same axis.
- State the period of Curve A. (1 mark)
- State the amplitude of curve B. (1 mark)
- Given that the first peaks of the two curves A and B are 30o apart, state the translation that maps curve B onto A.
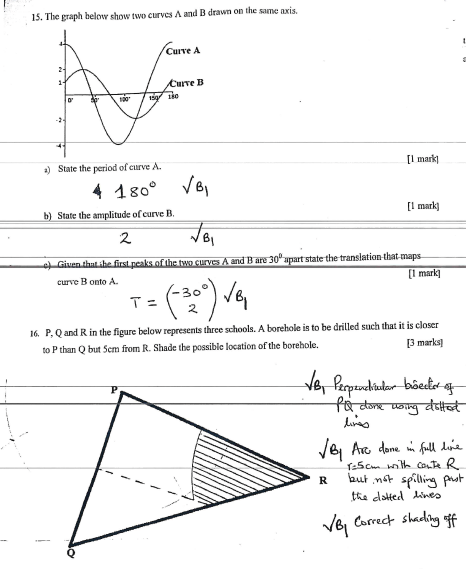
- P, Q and R in the figure below represents three schools. A borehole is to be drilled such that it is closer to P than Q but 5cm from R. Shade the possible location of the borehole. (3 marks)
SECTION II (50 marks)
Answer only five questions in this section in the spaces provided.
- The numbers 213, 205, 197,...,37 represents an Arithmetic Progression.
Determine the:- number of terms in the progression. (3 marks)
- eighteenth term of the progression. (2 marks)
- middle term of the progression. (3 marks)
- sum of the first 20 term of progression. (2 marks)
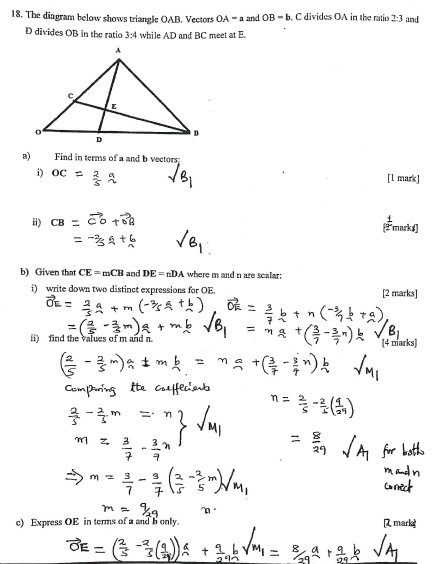
- The diagram below shows triangle OAB. Vectors OA = a and OB = b, C divides OA in the ratio 2:3 and D divides OB in the ratio 3:4 while AD and BC meet at E.
- Find in terms of a and b vectors:
- OC (1 mark)
- CB (2 marks)
- Given that CE = mCB and DE = nDA where m and n are scalar:
- Write down two distinct expressions for OE. (2 marks)
- find the values of m and n. (4 marks)
- Express OE in terms of a and b only. (1 mark)
- Find in terms of a and b vectors:
- In a certain country, the probability of school A topping in county exams is 1/3. If it tops the probabily of it topping in KCSE is 5/7 otherwise the probability of it topping in KCSE is 2/5. If the school tops in KCSE the probability of its appearing in the newspaper is 2/9, otherwise the probability of its appearing in newspaper is 4/11.
- Draw a tree diagram to represent the above information. (2 marks)
- Use the tree diagram to find the probabilty that:
- The school tops in the two exams and appears in the newspaper. (2 marks)
- The school did not appear in the newspaper. (2 marks)
- The school will appear in the newspaper anyway. (2 marks)
- The school tops in any one of the exams but does not appear in the newspaper. (2 marks)
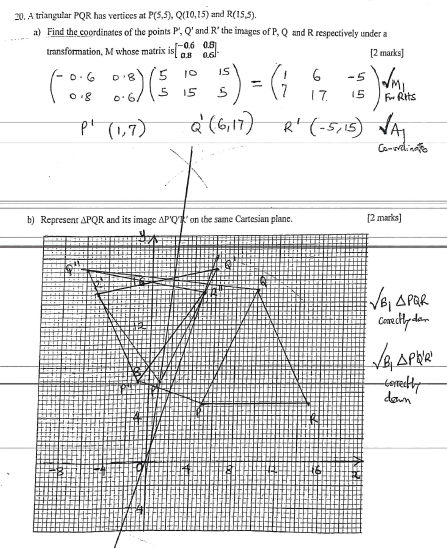
- A triangular PQR has vertices at P(5,5),Q(10,15) and R(15,5).
- Find the coordinates of the points P',Q' and R' the images of P, Q and R respectively under a transformation, M whose matrix is
(2 marks)
- Represent ΔPQR and its image ΔP'Q'R' on the same Cartesian plane. (2 marks)
- Triangle P'',Q'' and R'' is the image of P',Q' and R' under a reflection in the y-axis.
- Draw ΔP''Q''R'' on the same grid in (b) above and state the co-ordinates of the vertices. (2 marks)
- Describe fully a single transformation that maps ΔPQR onto ΔP''Q''R'' (2 marks)
- Determine a 2 x 2 matrix representing the transformation in c(ii) above. (2 marks)
- Find the coordinates of the points P',Q' and R' the images of P, Q and R respectively under a transformation, M whose matrix is
- On the surface of the earth, A(50oN, 80oE) and B(50oN,120oE) are two separate places. Given that the radius of the earth is 6370km, Π =22/7 and the local time at B is 12:30pm.
- Find the time at A. (2 marks)
- Calculate the shortest distance between A and B in km. (3 marks)
- If C(0o,80oE), find the distance between A and C in km. (3 marks)
- Another town D is 3000nm west of A, find its position. (2 marks)
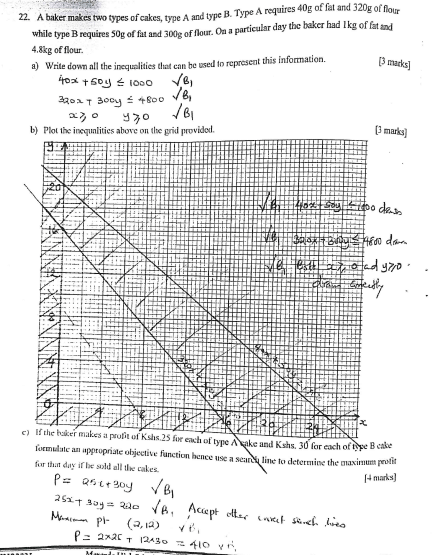
- A baker makes two types of cakes, type A and type B. Type A requires 40g of fat and 320g of flour while type B requires 50g of fat and 300g of flour. On a particular day the baker had 1kg of fat and 4.8kg of flour.
- Write down all the inequalities that can be used to represent this information. (3 marks)
- Plot the inequalities above on the grid provided. (3 marks)
- If the baker makes a profit of Kshs. 25 for each of type A cake and Kshs. 30 for each type B cake formulate an appropriate objective function hence use a search line to determine the maximum profit for the day if he sold all the cakes. (4 marks)
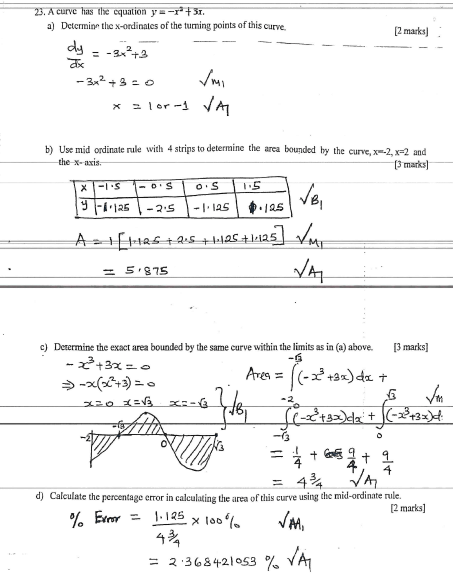
- A curve has the equation y =-x3 -3x
- Determine the x - ordinates of the turning points of this curve. (2 marks)
- Use mid-ordinate rule with 4 strips to determine the area bounded by the curve, x = -2, x = 2 and the x-axis. (3 marks)
- Determine the exact area bounded by the same curve within the limits as in (a) above. (3 marks)
- Calculate the percentage error in calculating the area of this curve using the mid-ordinate rule. (2 marks)
- The life expectancy in hours of 106 bulbs are shown in the table below.
Life Expectancy(hrs) 90-94 95-99 100-104 105-109 110-114 115-119 120-124 125-129 130-134 135-139 Frequency (f) 5 14 16 17 24 12 11 4 2 1 - Calculate the quartile deviation of the life expectancy of the bulbs. (4 marks)
- On the grid provided plot the ogive representing the information in the table above. (3 marks)
- Use the graph above to estimate the median life expectancy of the bulbs. (3 marks)

Marking Scheme
Download Mathematics Paper 2 Questions and Answers - KCSE Prediction Papers 2023.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students