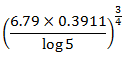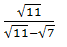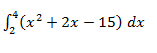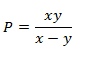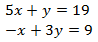MATHEMATICS PAPER 2 - 2017 MURANG'A MOCK EXAMINATION

SECTION I (50 Marks)

Answer all questions in this section

1. Use logarithms to evaluate;   (4 marks)
   

2. The equation of a line is -³/₅x + 3y = 6 . Find the
   1. Gradient of the line. (1 mark)
   2. Equation of a line passing through point and perpendicular to the given line. (3 marks)

3. A shirt whose marked price is sh. 800 is sold to a customer after allowing him a discount of 13%. If the trader makes a profit of 20%, find how much the trader paid for the shirt.  (3 marks)

4. Simplify      (2 marks)
   

5. The length and width of a rectangular signboard are (3x + 12)and (x-4) respectively. If the diagonal of the signboard is 200 cm, determine its area.  (4 marks)

6. Find the value of given that;  Log (x-1) + 2 = log (3x + 2) + log 25  (3 marks)

7. Use the expansion of (x-y)⁵ to evaluate correct to (9.8)⁵ 4 d.p.   (3 marks)

8. Evaluate (3 marks)
   

9. Make y the subject of formula:                                                                         (3 marks)
   

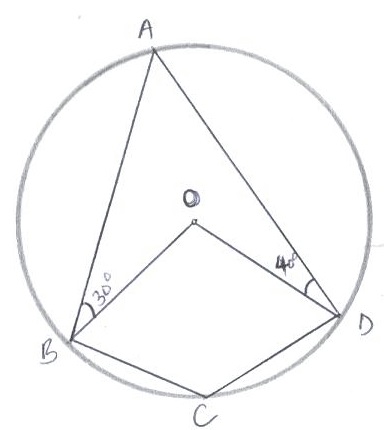
10. In the figure below, ABCD is a cyclic quadrilateral. Point O is the centre of the circle. <ABO = 30⁰ and <ADO = 40⁰ .Calculate the size of angle BCD.  (2 marks)
    

11. Find the number of terms of the series 2 + 6 + 10 + 14 + 18.... that will give a sum of 800.     (2 marks)

12. A bag contains 10 balls of which 3 are red, 5 are white and 2 are green. Another bag contains 12 balls of which 4 are red, 3 are white and 5 are green. A bag is chosen at random and then a ball chosen at random from the bag. Find the probability that the bell chosen is red.   (3 marks)

13. The point (5,2) undergoes the transformation   followed by a translation . Determine the coordinates of the image. (3 marks)

14. The latitude and the longitude of two stations A and B are and   Calculate the distance in nautical miles between A and B along latitude 47⁰ N.         (3 marks)

15. Using a ruler and a pair of compass only;
    1. Construct a parallelogram PQRS in which PQ = 6 cm, and QR = 4 cm and  (3 marks)
    2. Determine the perpendicular distance between PQ and SR.                       (1 mark)

16. The mass of a mixture A of beans and maize is 72 kg. The ratio of beans to maize is 3:5 respectively.
    1. Find the mass of maize in the mixture. (1 mark)
    2. A second mixture B of beans and maize of mass 98 kg is mixed with A. The final ratio of beans to maize is 8:9 respectively. Find the ratio of beans to maize in B. (3 marks)

SECTION II (50 Marks)

Answer any five questions in this section

17. Given the simultaneous equations
    
    
    1. Write the simultaneous equations in matrix form. Hence solve the simultaneous equations. (6 marks)
    2. Find the distance of the point of the intersection of a line 5x + y = 19 and -x + 3y = 9 from the point (11,-2) (4 marks)

18. A particle was moving along a straight line. The acceleration of the particle after t seconds was given by a = (9 - 3t)ms^-2. The initial velocity of the particle was 7 m/s. Find:
    1. The velocity (V) of the particle at any given time (t).  (4 marks)
    2. The maximum velocity of the particle. (3 marks)
    3. The distance covered by the particle by the time it attained maximum velocity.   (3 marks)

19. The figure below represents a right pyramid with vertex V and a rectangular base PQRS. PQ = 16 cm and QR = 12 cm. M and O are the mid points of QR and PR respectively. 
    
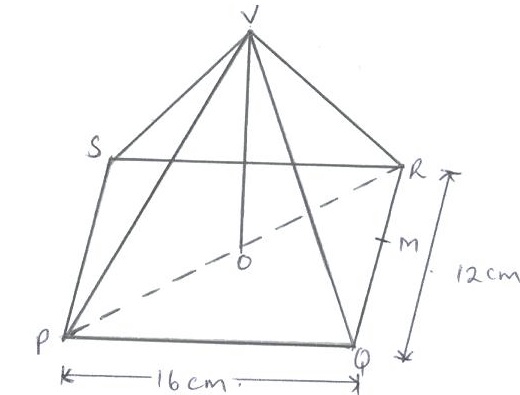
    Find;
    1. The length of the projection of line VP on the plane PQRS. (3 marks)
    2. The size of the angle between line VP and the plane PQRS. (3 marks)
    3. The size of the angle between the planes VQR and PQRS. (4 marks)

20. Two towns A and B lie on the same latitude in the northern hemisphere. When it is 8:00 a.m. at A, the time at B is 11:00 a.m.
    1. Given that the longitude of A is E, find the longitude of B.   (3 marks)
    2. A plane leaves A for B and takes hours to arrive at B travelling along a parallel of latitude at 850 km/h. Find
       1. The radius of the circle of latitude of towns A and B.  (4 marks)
       2. The latitude of the two towns. (3 marks)

21. The gradient function of a curve is given by the expression 2X+1. If the curve passes through the point (-4,6), 
    1. Find;
       1. The equation of the curve.  (3 marks)
       2. The values of x at which the curve cuts the x- axis. (3 marks)
    2. Determine the area enclosed by the curve and the x- axis.  (4 marks)

22. The transformation A given by the matrix  maps  to  and   to 
    1. Determine the matrix A giving a, b, c and d as fractions. (4 marks)
    2. Given that A represent a rotation through the origin, determine the angle of rotation. (3 marks)
    3. S is a rotation through 180⁰ about the point (2, 3). Determine the image of (1, 0) under followed by A. (3 marks)

23. The figure below shows a triangle ABC inscribed in a circle (not drawn to scale.) AB = 6 cm, BC = 9 cm and AC = 10 cm. 
    
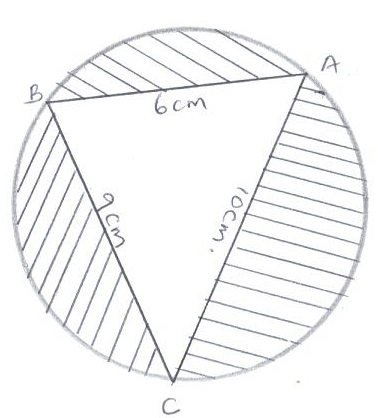
    Calculate;
    1. The radius of the circle. (6 marks)
    2. The area of the shaded parts.  (4 marks)

24. In an experiment involving two variables t and r, the following results were obtained.
    

    t	1.0	1.5	2.0	2.5	3.0	3.5
    r	1.50	1.45	1.30	1.25	1.05	1.00

    1. On the grid provided, draw the line of best fit for the data. (4 marks)
       
    2. The variables r and t are connected by the equation where a and k are constants. Determine;
       1. The values of a and k. (3 marks)
       2. The equation of the line of best fit.    (1 mark)
       3. The value of t when.   (2 marks)