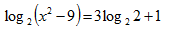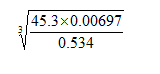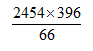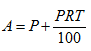MATHEMATICS PAPER 2 - KCSE 2019 MASENO MOCK EXAMINATION

INSTRUCTIONS TO CANDIDATES

• The paper consists of two sections: Section I and Section II.
• Answer all the questions in section I and any FIVE questions in section II.
• All working must be clearly shown
• Marks may be awarded for correct working even if the answer is wrong.
• Non-programmable silent electronic calculator and KNEC Mathematical Tabkles may be used.

Section I (50 Marks)
Answer all the questions in this section

1. Solve for x in  (3 marks)
   

2. Given that , find the values of p, q and r. (3 marks)

3. Expand (1-5x)⁵ up to the term in x⁵. Hence use your expansion to estimate (0.95)⁵ correct to 4 decimal places. (4 marks)

4. Solve for α in the equation  in the range 0⁰ ≤α ≤ 180⁰(4 marks)

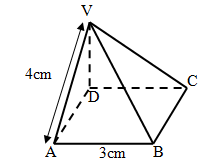
5. The diagram below represents a right pyramid on a square base of side 3cm. The slant edge of the pyramid is 4cm. 
   
   Calculate the angle between VA and the plane ABCD   (3 Marks)

6. The equation of a circle is x²+y²-8x+12y+16=0. Determine the coordinates of the centre of the circle and its radius. (3 marks)

7. Under a transformation whose matrix is  a figure whose area is 2.5cm² is mapped onto a figure whose area is 10cm². Find the two possible values of  and hence write down two possible matrices for T. (3 marks)

8. A mixture is made by mixing 4kg of long grain rice costing sh. 60 per kg with 9 kg of short grain rice costing sh. 50 per kg. How many kilograms of long grain rice should be added to the mixture so that the resulting mixture can be sold at sh. 66 per kg and a profit 20% is made.       (3 marks)

9. Sylvia invested a certain amount of money in a financial institution at a compound interest compounded quarterly. At the end of the third year it had amounted to sh. 18980 and by the end of the fifth year it had amounted to sh. 20530. Find the rate of interest.       (3 marks)

10. A variable Z varies directly as the square of X and inversely as the square root of Y. Find the percentage in Z if X is increased by 20% and Y decreased by 19%.(3 marks)
    

    Mass (kg)	Frequency
    40-44	4
    45-49	10
    50-54	15
    55-59	8
    60-64	3

11. The table below shows the masses of 40 students in a form 4 class.
    Calculate the quartile deviation correct to 1dp.   (3 marks)

12. Pipe A can fill an empty water tank in 3 hrs while pipe B can fill the same tank in 6 hrs. When the tank is full, it can be emptied by pipe C in 8 hrs. Pipes A and B are opened at the same time when the tank is empty. One hour later, pipe C is also opened. Find the total time taken to fill the tank.                                                 (3 marks)

13. Use logarithm tables to evaluate  (3 marks) 
                                                                     

14. By rounding off each number to the nearest tens, approximate the value of
    
    Hence calculate the percentage error arising from this approximation to 4 significant figures.   (3marks)

15. Make P the subject of the formula  (3 marks)
    

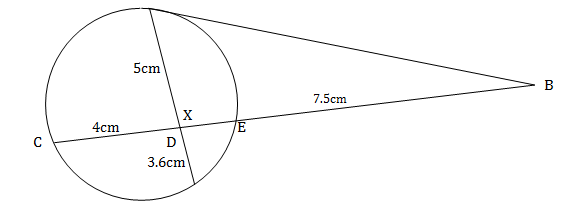
16. In the figure below, AB is a tangent, meetings chord CDE at B. DE = x cm. 
    
    Determine:
    1. the value of x.      (1 mark)
    2. the length of AB.  (2 marks)

Section II (50 marks)
Answer only five questions from this section

17. The third, fifth and eighth terms of an arithmetic progression are consecutive terms of a geometric progression. Given that the first term of the arithmetic progression is 8 determine,
    1. The common difference.        (2mks)
    2. The common ratio.                (2mks)
    3. The least number of terms of the arithmetic progression that gives a sum greater than 1525. 
    4. The sum of the first 10terms of the geometric progression.          (3mks)

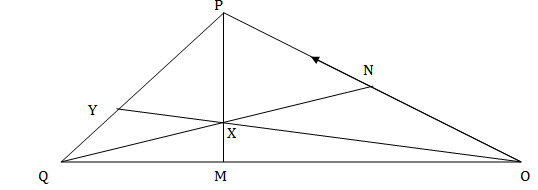
18. The figure below shows a triangle OPQ in which OP= P and  OQ= q. M and N are points on OQ and OP respectively such that ON : NP = 1 : 3 and OM : MQ = 2 : 1. 
    
    
    1. Express the following vectors in terms of P and q.                      (3 marks)
       1. PM
       2. ON
       3. PQ
    2. Line PM and QN intersect X such that PX =hPM and QX = k ON. Express OX in two different ways and hence find the values of h and K.     (6 marks)
    3. OX produced meets PQ at Y such that PY:YQ=3:2. Using the ratio theorem or otherwise. Find OY in terms of P and q.        (1 mark)

19. The probability that Peninah goes to school by bus is ¹/₃ and by matatu is ¹/₂. If she uses a bus the probability that she is late to school is ¹/₅ and if she uses a matatu the probability of being late to school is ³/₁₀. If she uses other means of transport the probability of being late is ¹/₂₀. 
    1. Draw a probability tree to represent this information.         (3mks)
    2. What is the probability that she will be late to school if she does not use a matatu.         (4mks)
    3. What is the probability that she will not be late to school.   (3mks)

20. The position of two towns A and B on the earth’s surface are (36⁰N, 49⁰E) and (36⁰N, 131⁰W) respectively.                                                                       
    1. Find the longitude difference between points A and B.               (1 mark)
    2. Given that the radius of the earth is 6370 km, calculate the distance in km between towns A and B         (Take π=²²/₇ ).
       1. along a circle of latitude. (2 marks)
       2. along a great circle. (3 marks)
    3. Another town C is 840km east of town B and on the same latitude as town A and B. Find the longitude of town C.(3 marks)
    4. The local time at town B is 11.00 a.m. Find the local time at town C.  (1 mark)
       

21. Complete the table below for the functions Y=2Sin x and y= 1- cosx, correct to 2 decimal places.   (2 marks)
    

    X0	00	300	600	900	1200	1500	1800
    2sin x				2
    1-cosx			0.5	1

    
    On the grid provided draw the graph of the functions y=2sinx and y=1-cosx on the same axes for 0⁰ ≤x≤ 180⁰. Use the scale; 2cm for 30⁰ on the x-axis and 2cm for 1 unit on the y-axis.  (5 marks)
    Use the graph to
    1. Solve the equation 2sinx + cos x = 1 (1 mark)
    2. Determine the range of values of x for which 2sinx ≥ 1 - cosx lie.       (1 mark)
    3. State the amplitude of y=2sinx from the graph.                                             (1 mark)

22. A cinema hall has seats for 400 people. The seats are in two categories; A and B which are charged at sh. 200 and sh. 500 per show respectively. The number of category B booked per show does not exceed that of category A. For the hall expenses to be covered at least 70 category B seats must be booked and they must be more than a quarter of the total number of seats booked.
    1. Other than x≥0 and y≥0, write down four inequalities to represent the condition satisfied by the seats per show.       (4 marks)
    2. Represent these inequalities on a graph.       (4 marks)
    3. If the hall is charged at sh. 45000 per day and the operation runs 3 hours per day, find the maximum possible profit per day.     (2 marks)
23.  
    1. Complete the table below for the function y=x²-3x-6 in the range -2≤x≤6 (1 mark)
       

       x	-2	-1	0	1	2	3	4	5	6
       y

    2. using the completed table and a suitable scale, draw the graph of y=x²-3x-6 in the grid provided below for -2≤x≤6  (3 marks)
    3. Use your graph to:
       1. Write down the roots of x²-3x-6=0 (1 mark)
       2. solve x²-5=0 (2 marks)
       3. Find the exact area bounded by the curve y=x²-3x-6, the x-axis, y-axis and the line x=3     (3 marks)

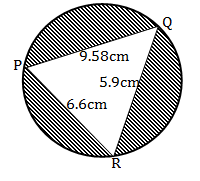
24. Triangle PQR is inscribed in the circle. PQ = 7.8cm, PR = 6.6cm and QR = 5.9cm. 
    
    Find;
    1. size of angle QPR (3 Marks)
    2. the radius of the circle. (3 Marks)
    3. the area of the shaded region. (4Marks)