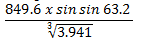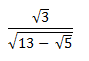MATHEMATICS PAPER 2 - 2019 KCSE CEKENA MOCK EXAMINATION (QUESTIONS AND ANSWERS)

INSTRUCTION TO STUDENTS:

• This paper consists of two Sections; Section I and Section II.
• Answer ALL the questions in Section I and only five questions from Section II.
• Show all the steps in your calculation, giving your answer at each stage in the spaces provided below each question.
• Marks may be given for correct working even if the answer is wrong.
• KNEC Mathematical tables may be used, except where stated otherwise.
• Candidates should answer the questions in English.

Ensure that all the pages are printed and no question(s) are missing.
SECTION 1   (50 Marks)
Answer all Questions from this Section

1. Use logarithms correct to 4 decimal places to evaluate. 4mks
   

2. A car was valued at ksh.500,000 in January 2017.Each year ,its value depreciates at 12% p.a.Find after how long would the value depreciate to 350,000 . 3mks

3. Simplify  (3mks)
   

4. Two fruits juices A and B are mixed together .Juice A cost sh.50 per litres.What is the ratio if the cost is sh.59 per litre of the mixture? 3mks

5. Find the centre and radius of the circle whose equations is
   x²+y² – 2x + 4y +1=0       3mks

6. Find the standard deviation for the following set of data 3mks
   16,42,41,6,20,28,19,23,15

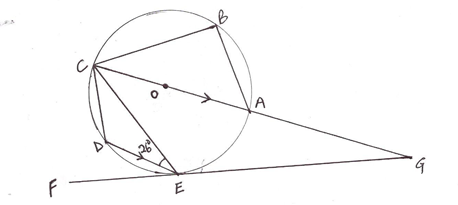
7. The diagram below shows a circle ABCDE .The line FEG is a tangent to the circle at point E.Line DE is parallel to CG.
   
   State giving reasons the sizes of;
   1. AEG                         2mks
   2. ABC                         2mks

8. Find the value of x given that log(x-2) + 2 =log (3x +1) + log 25 . 3mks

9. Find the percentage error in the calculation of the volume of a sphere whose radius is 4.9cm.     3mks

10. In a right angled triangle ,the two sides enclosing the right angle measure (3x -2) cm and (x+2)cm.If the area of the triangle is 36cm³.Find the length of these two sides. 3 mks

11.  
    1. Expand (a-b)⁵ 1mks
    2. Use the first three terms of the expansion in (a) in ascending power to find the approximate value of (1.98)⁵    (2mks)

12. The first term of geometric sequence is 16 ,and the fifth term is 81.Find the sum of the first 10 terms .     (3mks)

13. Solve the equation sin sin (¹/₂x-30)=cos cos x⁰  2mks

14. The angle at vertex of a cone is 90⁰.If the slant height is √4 cm,find without using tables .
    1. The diameter of the cone      2mks
    2. The height of the cone.     2MKS

15. Under a transformation whose matrix is Q = (x-2 -2x²),a triangle whose area is 12cm² is mapped onto a triangle whose area is 50cm².Find the two possible values of a . 3mks

16. Make L the subject of the formula below.
    f=      2mks

SECTION B(50MKS)Answer only five questions from this section

17.  
    1. Complete the table given below by filling the blank spaces. 2mks
       

       X	0	15	30	45	60	75	90	105	120	135	150	165	180
       4cos 2x	4.00		2.00	20				-3.46	-2.00	0	-2.00		4.00
       2sin(2x+30)	1.00	1.73	2.00	1.73		0	-1.00	-1.73	-.2.00	-1.73		0	1.00

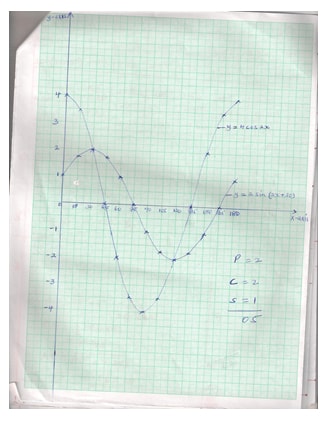
    2. On the grid provided draw the graph of y = 4cos 2xn and y =2 sin (2x+30) for O⁰ ≤x≤180⁰ . 5mks
    3.  
       1. State the amplitude of y=4cos 2x .      1mk
       2. Find the period of y =2sin (2x+30)⁰
    4. Use your graph to solve
       4cos 2x -2sin (2x+30) =0       1mk

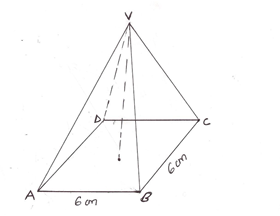
18. The figure below is a square based pyramid ABCDV with AD=DC=6cm and height VO=10cm.
    
    
    1. State the projection of VA on the base ABCD                                  1mk
    2. Find
       1. The length of VA .             3mks
       2. The angle between VA and ABCD .                          2mks
       3. The angle between VDC and ABCD 2mks
       4. Volume of the pyramid.                                 2mks

19. The table below gives marks obtained in a mathematics test by 47 candidates.
    

    Marks	31-35	36-40	41-45	46-50	51-55	56-60
    No of candidates	4	6	12	15	8	2

    
    
    1. Calculate the mean score                    3mks
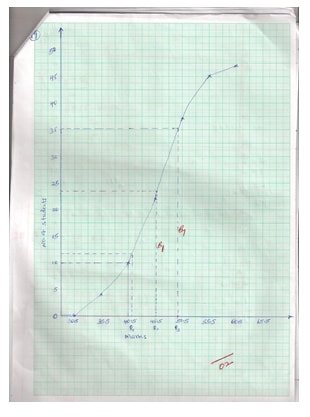
    2. On the grid provided draw a cumulative frequency graph and use it to estimate
       1. The median 2mk
       2. The semi-interquartile range. 3mks
    3. In order to pass the test a pupil had to score more than40 marks. Calculate the percentage of pupils who passed.         2mks

20.  
    1. In a form 4 Class there are 22 girls and 18 boys. The probability that a girl completes the secondary education course is³/₅ whereas that of a boy is ²/₃ .A student is picked at random from the class .Find the probability that the student picked
       1. Is a boy and will complete the course. 2mks
       2. Will complete the course. 2mks
       3. Is a girl and will not complete the course. 2mks
    2. A bag contains 5 blue balls, 8 red balls and 3 green balls being similar in shape and size .A ball is picked out at random without replacement and its colour noted, use a tree diagram to determine the probability that at least one of the first two balls picked is green.             4mks

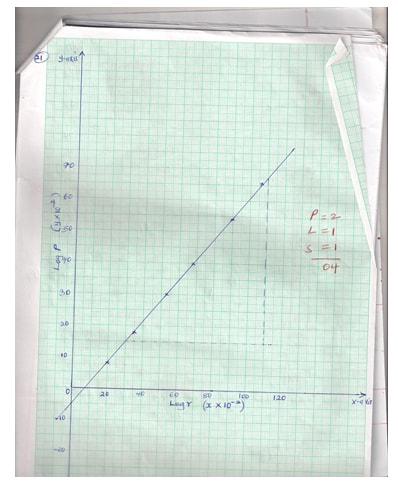
21. Two quantities P and R are connected by the equation P=Krⁿ where k and n are constants. The table of values of P and r is given below.
    1. State the linear equation connecting P and r.       1mk
    2.  
       1. Using a suitable scale draw a suitable line graph from the above data on the grid provided .              5mks
       2. Using your graph estimate the values of k and n.         3mks
    3. Find the equation connecting P and r.                                                                                    1mk

22.  
    1. P,Q and R are three quantities such that P varies directly as the square of Q and inversely as the square root of R.
       1. Given that P=12 when Q=24 and R=36,find P when Q=27 and R=121.          3mks
       2. If Q increases by 10% and R decreases by 35% find the percentage increase in P.        4mks
    2. If Q is inversely proportional to the square root of P and P=4 when Q=3.Calculate the value of P when Q = -8. 3MKS                                                                                             

23. A community water tank is in the shape of a cuboid of base 6m by 5m and a height of 4m.A feeder pipe of diameter 14cm suppliers water to this tank at the rate of 40cm /s
    Calculate the;
    1. Capacity of the tank in litres. 2mks
    2. Amount of water ,in litres delivered to this tank in one hour. 3mks
    3. The time taken for the tank to fill . 2mks
    4. The community consumes a full tank a day,with each family consuming an average of 150 litres per day.If each family pays a uniform rate of sh.350 per month,find the total amount of money due monthly. 2mks

24. In the diagram O is the centre of a circle radius 11cm .OX=5cm and BX=12cm.
    
    
    1. Find the length of XA. 3mks
    2. Find the size of angle XOA . 3mks
    3. Find the area of the shaded part. 4mks

MARKING SCHEME