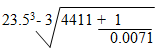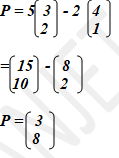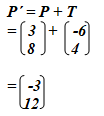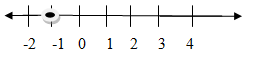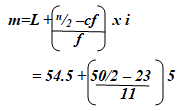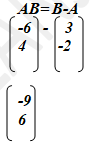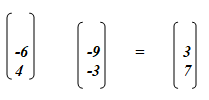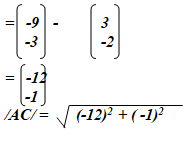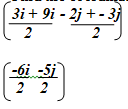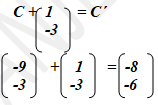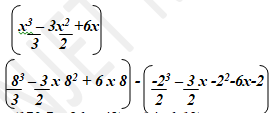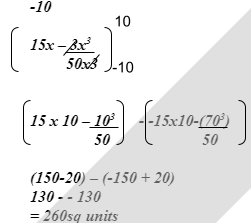INSTRUCTIONS TO THE CANDIDATES
- This paper contains two sections; Section I and Section II.
- Answer all the questions in section I and only five questions from Section II.
- All workings and answers must be written on the question paper in the spaces provided below each question.
- Non programmable silent electronic calculators and KNEC Mathematical tables may be used EXCEPT where stated otherwise.
- Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
Section I (50 marks)
Answer All the questions in this section
- Evaluate without using tables or calculators (2mks)
⁶/₇ of ¹⁴/₃ ÷ 80 x –²⁰/₃
−2 x 5 ÷ (14 ÷ 7 ) x 3 - The line y = 3x + 3 meets the line L1 at the point (2, 9) and at right angles. Find the points at which the two lines intersect with the x- axis. (3mks)
- Given that p = 5a – 2b where a =
and b =
, find :
- Column vector p. (2mks)
- P' the image of p under a translation vector
(1mk)
- Solve the following inequalities and represent the solution on a number line. (3mks)
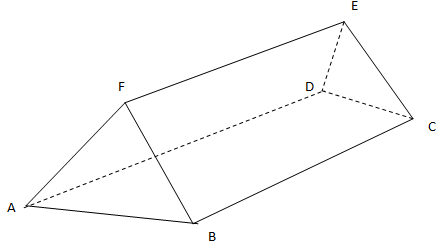
4x – 3 ≤ 6x -1 < 3x + 8 - The figure below shows a triangular prism of uniform cross section. AF=FB= 4cm. AB=7cm, BC= 12cm. given that angle BAF=30°, find the total surface area of the prism. (3mks)
- Use tables of cubes, cubes roots and reciprocals to evaluate; (4mks)
- The density of a substance A is given as 13.6g/cm3 and that of a substance B as 11.3g/cm3. Determine, correct to one decimal place, the volume of B that would have the same mass as 50cm3 of A. (3mks)
- Find x in 2(4x) – 10 (2x) + 8 = 0 (3mks)
- The sum of interior angles of a regular polygon is 24 times the size of the exterior angle.
Find the number of sides of the polygon. (3mks) - Triangle ABC has its vertices at A(3, 0), B(2,3) and C(5,1) if A΄(5, 0), B΄(3,6) and C΄(9,2) is the image of ABC under enlargement. On the same axes and grid provided below, determine the centre of enlargement and linear scale factor. (3mks)
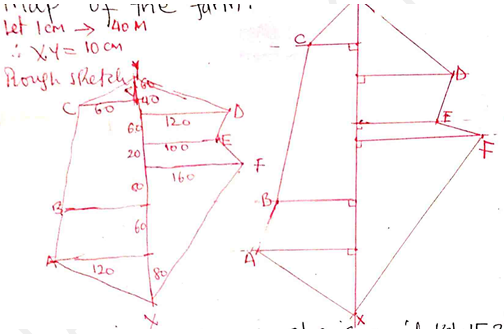
- The following measurements were recorded in a field book of a farm using XY as the base line XY=400M.
Using a suitable scale, draw an accurate map of the farm. (4mks)Y C60
B100
A120340
300
240
220
140
80
120D
100E
160E
X - Waceke is a saleslady. She is paid Ksh15,375 per month. She is also paid a commission of 4½ % on the amount of money she makes from her sales. In a certain month, she earned a total of Ksh. 28,875. Calculate the value of her sales that month. (3mks)
- Two buses P and Q leave Kisumu at 7.30am and 9.30am respectively. If their speeds are 60km/h and 100km/h respectively,find when Q catches up with P. (3mks)
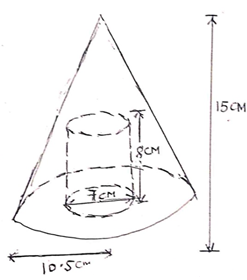
- The figure below shows a solid cone. It has a cylindrical hole drilled into it. The diameter of the hole is 7cm and its height 8cm. The radius of the cone is 10.5cm and its vertical height is 15cm.
Calculate the volume of the solid. (3mks) - Simplify completely: (3mks)
(a +2b)² – ( 2a – b)²
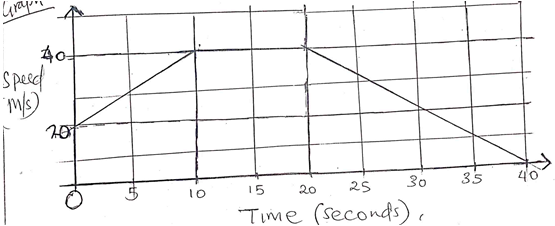
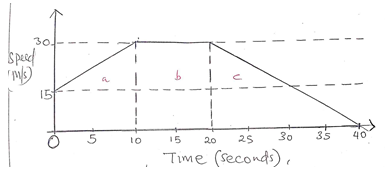
ab² – a² - The figure below represents a speed time graph for a cheetah in 40 seconds.
Calculate the total distance covered by the cheetah. (3mks)
SECTION II
Answer any five questions in this section.
- A rectangular tank whose internal dimensions are 2.4m by 2.5m by 3.7m is two thirds full of juice.
- Calculate the volume of the juice in litres. (3mks)
- The juice is parked in small packets in a shape of right pyramid with equilateral triangles of sides 20cm. the height of each packet is 15cm. a full packet is sold at kshs. 50 per packet.
Calculate:- The volume of the juice in cm3 of each packet to the nearest whole number. (3mks)
- The number of full packets of juice. (2mks)
- The amount of money realized from the sale of juice. (2mks)
- The masses in kilograms of patients who attended a clinic on a certain day were recorded as follows.
67 49 57 58 69 58 39 61 51 47 38 59 46 52 60 72 59 49 54 52 69 62 58 67 63 59 65 58 49 44 49 41 70 58 54 60 60 59 42 41 79 52 51 48 54 59 62 73 48 54 - Starting with the class 35-39, make a frequency distribution table for the data. (2mks)
-
- Calculate the mean mass. (3mks)
- Calculate the median mass. (3mks)
- On the grid provided draw a frequency polygon to represent the data. (2mks)
- The position vectors of A, B and C are 3i – 2j, -6i + 4j and -9i – 3j respectively.
- State the column vectors.
- AB (2mks)
- CB (2mks)
- Find the distance from A to C. (2mks)
- Find the coordinates of the mid point of AC. (2mks)
- If point C' is the image of C under translation vector
Find the co-ordinates of C'. (2mks)
- State the column vectors.
- Complete the table below for the function y= x2– 3x + 6 in the range -2 ≤ x ≤ 8. (2mks)
X −2 −1 0 1 2 3 4 5 6 7 8 Y - Use the trapezium rule with 10 strips to estimate the area bounded by the curve, y=x2− 3x + 6, the lines x = −2, x =8 and the x – axis. (3mks)
- Use the mid – ordinate rule with 5 strips to estimate the area bounded by the curve, y = x2 – 3x + 6, the lines x = −2, x = 8 and the x- axis. (3mks)
- By integration, determine the actual area bounded by the curve y = x2 – 3x + 6, the lines x = −2, x = 8, and the x – axis. (3mks)
- The corner points A, B, C and D of a ranch are such that B is 8km directly East of A and C is 6km from B on a bearing of 30°. D is 7km from C on a bearing of 30°.
- Using a scale of 1cm to represent 1km, draw a diagram to show the positions of A, B, C and D. (4mks)
- Use the scale drawing to determine:
- The bearing of A from D. (1mk)
- The distance BD in kilometers. (2mks)
- The perimeter of the ranch in kilometers. (3mks)
- Johana and MuchirucontributesKsh. 150,000 and Ksh. 180,000 every year respectively for a business, after one year Jacob joined the business and contributed Ksh. 135,000.
- Calculate the ratio of their investment after three years of business. (3mks)
- They agreed that 30% of the profits after 3 years be used to cater for the costs of running the businesses while the remaining would be shared proportionally. Calculate each person’s share if the profit after 3 years was shs. 240,000. (4mks)
- If each re-invested their shares back into the business, find the new individual investment at the beginning of the fourth year. (3mks)
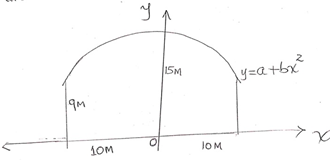
- The figure below shows the end wall of a building with the axes shown and 1M as the unit of measurement. The roof line is given by y= a + bx2, where a and b are constants.
- State the value of a. (1mk)
- Calculate the value of b. (3mks)
- Calculate the values of y for x = 2, 4, 6, 8 and compete the table below. (2mks)
X −10 0 2 4 6 8 10 Y 9 15 9 - Calculate the area of the wall. (4mks)
- A ball is thrown upwards and its height after t seconds is 5 meters, where s = 20t – 5t2. Find
- The greatest height reached and the time when it is reached. (3mks)
- The time when it returns to the original level. (3mks)
- Its velocity after 3 seconds. (2mks)
- Its acceleration during the throw. (2mks)

MARKING SCHEME
- Evaluate without using tables or calculators (2mks)
⁶/₇ of ¹⁴/₃ ÷ 80 x –²⁰/₃
−2 x 5 ÷ (14 ÷ 7 ) x 3
6/7 x 14/3 = 4
4 ÷ 80 = 4/80
4/80 x = 20/3 =−1/3
−2 x 5 ÷ 2 x 3
−2 x 5/2 x 3
−15
−¹/₃
−15
−1/3 ÷ −15/1 M1 – num/den
−1/3 x 1/45 M1 – single fraction
=1/45 - The line y = 3x + 3 meets the line L1 at the point (2, 9) and at right angles. Find the points at which the two lines intersect with the x- axis. (3mks)
G1=3
G2= −1/3
Equation L2
y-9 = -1
x-2 3
3y – 27 = −x +2
3y= −x +29
y=−1/3 x + 29/3
at x –axis, y=0
4 → 0= 3x + 3
3x = −3
X = 11
( −1, 0)
for L2
0= −1/3x + 29/3
1/3x = 29/3
x = 29
(29,0) -
-
-
- Ux – 3 ≤6x – 1
-2x ≤ 2
x≥-1 - 6x -1<3x+8
3x<9
X<3
-1≤x<3
- Ux – 3 ≤6x – 1
- The figure below shows a triangular prism of uniform cross section. AF=FB= 4cm. AB=7cm, BC= 12cm. given that angle BAF=30°, find the total surface area of the prism. (3mks)
Area of Δ faces = ½ x 4x 4 x sin120 x 2
= 13.856
= 14cm2
Area of rectangles = 12 x 4 x 2+12 x 6
= 96+72
=168
Total S.A =168 + 13.856
= 181.856 accept 182cm2
= 181.9cm2
Alternative
h=√(42 - 352)
=√(16-12.25)
=1.94cm
Area of triangular
Faces = ½ x 1.94 x 7x2
=13.587cm2
Total = 168+13.587
=181.58 = 181.6cm2 - (2.35 x 101)3 - 3√(4.411 x 103)+ 1
7.1 x 10-3
12.978 x 103 – 1.64 x 10 + 0.1408 x 103
12,978 – 16.4 + 140.8 = 13,102.4 - D = m/v
Mass of A = 50cm3 x 13.6g/cm3 = 680g
Mass of B = 680g
Density = 11.3g/cm3
Volume of B = 680g
11.3g/cm3
= 60.2cm3 - 4x − 5(2x) + 4 = 0
(22)x – 5 (2x)+4 = 0
Let 2x be u
U2 – 5u + 4 =0
(−4, −1)
u2 − 4u – u + 4 = 0
u(u – 4) -1 (u – 4) = 0
(u – 1 ) (u – 4) = 0
u = 1 or 4
2x = 1 = 20
X = 0
also:
2x = 4 = 22
x = 2
x = 0
and
2 - The sum of interior angles of a regular polygon is 24 times the size of the exterior angle.
Find the number of sides of the polygon. (3mks)
(2n – 4) 90= 24 x 360/n
180n – 360 = 8640
n
180n2 – 360n = 8640
n2 – 2n – 48 =0
-48 = -8 x 6
- 2 = -8+6
(n – 8) (n + 6) = 0
n=8
Or
-6
8 sides - Triangle ABC has its vertices at A(3, 0), B(2,3) and C(5,1) if A΄(5, 0), B΄(3,6) and C΄(9,2) is the image of ABC under enlargement. On the same axes and grid provided below, determine the centre of enlargement and linear scale factor. (3mks)
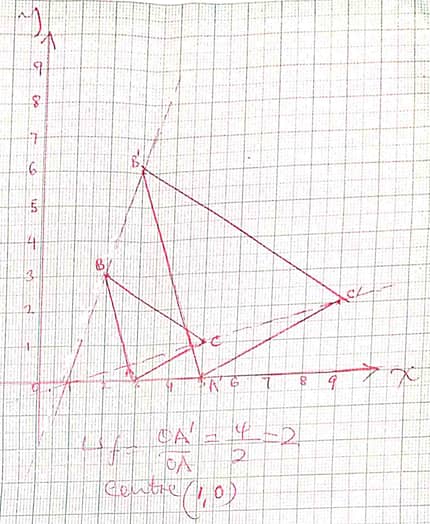
- The following measurements were recorded in a field book of a farm using XY as the base line XY=400M.
Y C60 1.5cm
B100 2.5cm
A120 3cm340 8.5cm
300 7.5cm
240 6cm
220 5.5cm
140 3.5cm
80 2cm
120D 3cm
100E 2.5cm
160F 4cm
X - Waceke is a saleslady. She is paid Ksh 15,375 per month. She is also paid a commission of 4 ½ % on the amount of money she makes from her sales. In a certain month, she earned a total of Ksh. 28,875. Calculate the value of her sales that month. (3mks)
Earnings on sales = 28875 – 15375
= sh 13,500
4 ½ % of y = 13500
Y= 100 x 13500
4.5
Y = sh 300,000 - Two buses P and Q leave Kisumu at 7.30am and 9.30am respectively. If their speeds are 60km/h and 100km/h respectively, find when Q catches up with P. (3mks)
Distance by p in 2hrs
60 x 2 = 120km
RS= 100-60 60
= 40Km/hr
Time to overtake
= 120 = 3hrs
40
9.30 + 3hrs = 12.30p.m
alternative method
distance by P = y km
time = (y/60)hrs
distance by Q = 120 + y
time = 120 + y
100
100y = 7200 + 60y
40y = 7200
y= 180km
time= 180 =3hrs
60
time to catch
up = 9.30 + 3 = 12.30p.m - The figure below shows a solid cone. It has a cylindrical hole drilled into it. The diameter of the hole is 7cm and its height 8cm. The radius of the cone is 10.5cm and its vertical height is 15cm.
Calculate the volume of the solid. (3mks)
Volume of the cone – volume of cylinder M1-values subst in formula
1/3πR2H – πr2h M1-simplifying
π(1/3 x 10.52 x 15 – 3.52 x 8) A1
π(551.25 – 98)
453.25π
=1424.5cm3 - let a + 2b =x
2a – b = y
x2−y2 = (x + y) (x−y)
(a+2b+2a-b) (a+2b)−(2a−b))
(3a+b) (−a+3b)
(3a+b) (3b-a)
(3b)2 –a2
(3b+a)(3b-a)
(3b+a)(3b-a)
(3a+b)(3b–a)
3a+b
3b+a - The figure below represents a speed time graph for a cheetah in 40 seconds.Calculate the total distance covered by the cheetah. (3mks)
Area of a = ½ x 10 (15+30)
= 225m
Area of b = 30 x 10
= 300m = 825m
area of c = ½ x 30 x 20
= 300m
total = 225 + 300 + 300
= 825m - A rectangular tank whose internal dimensions are 2.4m by 2.5m by 3.7m is two thirds full of juice.
- Calculate the volume of the juice in litres. (3mks)
2/3 x 2.4 x 2.5 x 3.7
14.8m3
1m3 → 1000L
14.8m3 → ?
14.8 x 1000
14800 litres - The juice is parked in small packets in a shape of right pyramid with equilateral triangles of sides 20cm. the height of each packet is 15cm. a full packet is sold at kshs. 50 per packet.
Calculate:- The volume of the juice in cm3 of each packet to the nearest whole number. (3mks)
Base area
=½ ab sin C
= ½ x 20 x 20sin 60
= 173.21
Vol = 1/3 x 173.21 x 15
= 866.025
= 866 cm3 - The number of full packets of juice. (2mks)
1m3 = 1000000cm3
14.8m3 = ?
14.8 x 1000000cm3
No of packets = 14.8x106
866
=17089.58
=17,089 - The amount of money realized from the sale of juice. (2mks)
17089 x 50 = Sh. 854,450
- The volume of the juice in cm3 of each packet to the nearest whole number. (3mks)
- Calculate the volume of the juice in litres. (3mks)
- The masses in kilograms of patients who attended a clinic on a certain day were recorded as follows.
- Starting with the class 35-39, make a frequency distribution table for the data. (2mks)
Mass F Mid(x) ƒx cƒ 35-39 2 37 74 2 40-44 42 168 6 45-49 47 376 14 50-54 52 468 23 55-59 57 627 34 60-64 62 434 41 65-69 67 335 46 70-74 72 216 49 75-79 77 77 50 Σƒ = 50 Σƒx = 2775 -
- Calculate the mean mass. (3mks)
X = Σƒx
Σƒ
= 2775
50
=55.5kg - Calculate the median mass. (3mks)
= 54.5 +0.91
= 55.41
- Calculate the mean mass. (3mks)
- On the grid provided draw a frequency polygon to represent the data. (2mks)
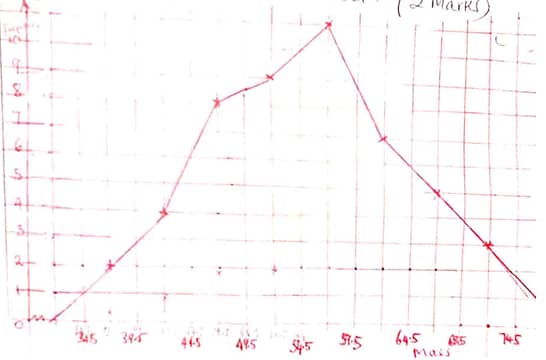
- Starting with the class 35-39, make a frequency distribution table for the data. (2mks)
-
-
- AB (2mks)
- CB (2mks)
CB = B-C
- AB (2mks)
- Find the distance from A to C. (2mks)
AC = C−A
√145
= 12.04 units A1 - Find the coordinates of the midpoint of AC. (2mks)
= -3i, -2.5j
Point (-3, -2.5) - If point C΄ is the image of C under translation vector 1
Find the co-ordinates of C΄. (2mks)
C΄ = (-8, -6) or -8i -6j
-
-
X −2 −1 0 1 2 3 4 5 6 7 8 Y 16 10 6 4 4 6 10 16 24 34 46 Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y8 Y9 Yn - Use the trapezium rule with 10 strips to estimate the area bounded by the curve, y=x2 - 3x + 6, the lines x = -2, x =8 and the x – axis. (3mks)
Let h=1
= ½h (Y0 +Yn +2 (y1+y2+…)
=0.5(16+46+2(10+6+4+4+6+10+16+24+34)
=0.5 (62+228)
=145 square units - Use the mid – ordinate rule with 5 strips to estimate the area bounded by the curve, y = x2 – 3x + 6, the lines x = -2, x = and the x- axis. (3mks)
A = h(y1+y2+……..yn)
= 2 (10 + 4 + 6 + 16 + 34)
= 140 sq units - By integration, determine the actual area bounded by the curve y = x2 – 3x + 6, the lines x = -2, x = 8, and the x – axis. (3mks)
Intergrate form -2 to 8 (x2 – 3x +6).dx
(170.7 – 96 + 48) – (-4 -6-12)
122.7 + 22 M1
= 144.7 sq units
- Use the trapezium rule with 10 strips to estimate the area bounded by the curve, y=x2 - 3x + 6, the lines x = -2, x =8 and the x – axis. (3mks)
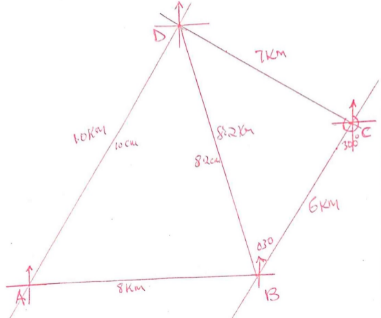
- The corner points A, B, C and D of a ranch are such that B is 8km directly East of A and C is 6km from B on a bearing of 30°. D is 7km from C on a bearing of 300°.
- Using a scale of 1cm to represent 1km, draw a diagram to show the positions of A, B, C and D. (4mks)
- Use the scale drawing to determine:
- The bearing of A from D. (1mk)
= 180 + 30
= 201°
±1° - The distance BD in kilometers. (2mks)
8.2cm
8.2 x 1km
=8.2km B1
±0.1 - The perimeter of the ranch in kilometers. (3mks)
AD = 10cm = 10km
P = 8km + 6km +7km + 10km
=31km
- The bearing of A from D. (1mk)
- Using a scale of 1cm to represent 1km, draw a diagram to show the positions of A, B, C and D. (4mks)
- Johana and Muchiru contributes Ksh. 150,000 and Ksh. 180,000 every year respectively for a business, after one year Jacob joined the business and contributed Ksh. 135,000.
- Calculate the ratio of their investment after three years of business. (3mks)
Muchiri’s contribution = 180000 x 3 = 540,000
Johana’s contribution = 150000 x 3 = 450,000
Jacob’s contribution = 135000 x 2 = 270,000
Ratio Johana: Muchiri: Jacob
= 450,000: 540,000: 270,000
= 5:6:3 - They agreed that 30% of the profits after 3 years be used to cater for the costs of running the businesses while the remaining would be shared proportionally. Calculate each person’s share if the profit after 3 years was shs. 240,000. (4mks)
30/100 x 240000 = 72000
Remainder = 240000 - 72000
= 168000
5:6:3
5 + 6 + 3 =14
Johana’s = 5/14 x 168000 = 60000
Muchiri = 6/14 x 168000 = 72000
Jacobs = 3/14 x 168000 = 36000 - If each re-invested their shares back into the business, find the new individual investment at the beginning of the fourth year. (3mks)
Johana’s = 450000 + 60000 = 510000
Muchiri’s = 540000 + 72000 = 612000
Jacob’s = 270000 + 36000 = 306000
- Calculate the ratio of their investment after three years of business. (3mks)
- The figure below shows the end wall of a building with the axes shown and 1M as the unit of measurement. The roof line is given by y= a + bx2, where a and b are constants.
- State the value of a. (1mk)
A = y intercept
A= 15 - Calculate the value of b. (3mks)
Y = 15 + bx2
At x = −10, y=9 (−10,9)
9= 15 + (−102)b
9= 15 + 100b
100b = 9 − 15
=−6
B=−6/100 = −3/50
Or = 0.06 - Calculate the values of y for x = 2, 4, 6, 8 and compete the table below. (2mks)
Y = 15 – 3x2X −10 0 2 4 6 8 10 Y 9 15 14.76 14.04 12.84 11.16 9
50 - Calculate the area of the wall. (4mks)
10(15 – 3x2) dx
50
- State the value of a. (1mk)
- A ball is thrown upwards and its height after t seconds is 5 meters, where s = 20t – 5t2. Find
- The greatest height reached and the time when it is reached. (3mks)
Velocity (v) = ds
dt
v = 20 – 10t
at maximum, v=0
20 – 10t =0
T=2 seconds
S=20(2) – 5 (22)
= 40 – 20
=20m - The time when it returns to the original level. (3mks)
At original level1 s=0
20t – 5t2=0
5t (4 – t) =0 M1-eqn
T=0 or 4 sec M1
After 4 seconds A1 - Its velocity after 3 seconds. (2mks)
V = 20 – 10t
V = 20 – 10(3)
= 20 – 30 M1-substuted
= – 10m/s A1 - Its acceleration during the throw. (2mks)
If V= 20 – 10t
Acceleration = dv/At
=– 10ms– 2
- The greatest height reached and the time when it is reached. (3mks)
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - Lanjet Mock Exams 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students