Mathematics Paper 1 Questions and Answers - MECS Cluster Joint Mock Exams 2021/2022

MATHEMATICS
PAPER 1

INSTRUCTIONS TO CANDIDATES

• Write your name, index number and class in the spaces provided above.
• The paper contains two sections: Section I and Section II.
• This paper contains 14 PRINTED pages make sure all PAGES ARE PRINTED and NON IS MISSING
• Answer ALL the questions in Section I and ANY FIVE questions from Section II.
• All working and answers must be written on the question paper in the spaces provided below each question.
• Marks may be awarded for correct working even if the answer is wrong.
• Negligent and slovenly work will be penalized.
• Non-programmable silent electronic calculators and mathematical tables are allowed for use.

SECTION I (50 MARKS)
Answer all the questions in this section in the spaces provided.

1.          
   1. Evaluate 94344 – 36425 ÷ 5 (1mark)
   2. Write the total value of the digit in the thousands place of the result obtained in (a) above (1mark)
2. In a game park ¹/₅ of the animals are rhinos and ¾ of them are zebras. 23 of the remaining animals are lions and the rest are warthogs. Find the fraction of warthogs in the game park. (3marks)
3. The volume of a cube is 2744cm³. Calculate the length of the diagonal of a face of the cube giving your answer in surd form. (3marks)
4. Without using mathematical tables or a calculator, evaluate
   27^²/₃ x (⁸¹/₁₆) ^-³/₄(3marks)
5. Using ruler and a pair of compasses only, construct triangle ABC in which AB = 6cm and angle ABC = 105º and angle BAC = 45º. Measure length of BC. (3marks)
6. An empty specimen bottle has a capacity of 300ml and a mass of 280g. Calculate the mass of the bottle when it is full of a liquid whose density is 1.2g/cm³. (3marks)
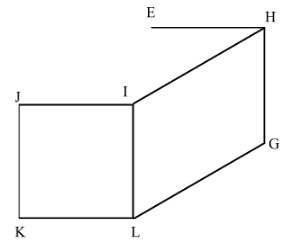
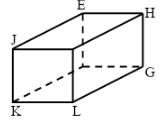
7. The figure below shows a sketch of a solid cuboid EFGHIJKL. Complete the sketch. (2marks)
   
8. Find the rate per annum at which a certain amount doubles after being invested for a period of 5 years compounded semi-annually (3marks)
9. The sum of the interior angles of a regular polygon is 40 times the size of the exterior angle.
   1. Find the number of sides of the polygon. 3marks
   2. Name the polygon 1mark
10. The data below shows the number of pupils in Nairutia Primary School
    42   43   48   40   46   42   44   48   39   40   42
    41   47   46   45   49   45   42   40   38   39   40
    46   47   42   40   41   43   44   45   46   48
    1. Using a class size of 2 organize the data in a grouped frequency table. 2marks
    2. Determine the mean of the data. 2marks
11. Given that q = 5t – 3f where t = (-2   -3) and f = (1     -2) find:
    1. the column vector q (2marks)
    2. Given that T^I (3,2) is the image of T (0,-2) under a translation, find the translation. (1mark)
12. Given that a = -5 b = 3 and c = ^-1/₃, evaluate:(3marks)
       5a²- 2b-4c   
      ¹/₃(b²+2a) 
13. Find the value of x in the equation Cos(3x -180º)= ^√3/₂ in the range listed below. (3marks)
    0º ≤ x ≤ 180º
14. Simplify the expression (3marks)
        4t²-25a²    
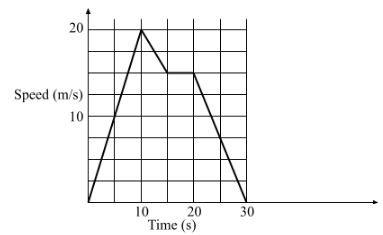
    6t²+9at-15a² 
15. The figure below represents the speed-time graph of a tuktuk. Use it to answer the questions (a) and (b)
    
    
    1. Calculate the acceleration of the tuktuk. (2marks)
    2. Find the total distance travelled for the whole journey (2marks)
16. A farmer has a piece of land measuring 840m by 396m. He divides it into square plots of equal size. Find the maximum area of one plot. (3marks)

SECTION II(50 MARKS)
Answer any five questions in this section in the spaces provided.

17. In the year 2001 the price of a sofa set in a shop was KSh. 12,000
    1. Calculate the amount received from the sales of 240 sofa sets that year. (2marks)
    2. In the year 2002 the price of each sofa set increased by 25% while the number of sets sold decreased by 10%.
       1. Calculate the percentage increase in the amount received from the sales (3marks)
       2. If at the end of the year 2002, the price of each sofa set changed in the ratio 16:15.
          Calculate the price of each sofa set in the year 2003. (2marks)
    3. The number of sofa sets sold in the year 2003 was p% less than the number sold in the year 2002. Calculate the value of P given that the amount received from the sales in the year were equal (3marks)
18. A line L passes through points (-2,3) and (-1,6) and is perpendicular to a line P at (-1,6)
    1. Find the equation of L. (2marks)
    2. Find the equation P in the form ax + by = c where a, b and c are constants. (2marks)
    3. Given that another line Q is parallel to L and passes through point (1,2), find the x and y - intercepts of Q. (3marks)
    4. Find the point of intersection of lines P and Q. (3marks)
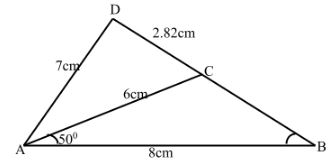
19. In the figure below (not drawn to scale) AB = 8cm, AC = 6cm, AD = 7cm, CD = 2.82cm and angle CAB = 50º.
    
    Calculate to 2 decimal places
    1. the length BC (3marks)
    2. the size of angle ABC (2marks)
    3. the size of angle CAD (3marks)
    4. the area of triangle ACD (2marks)
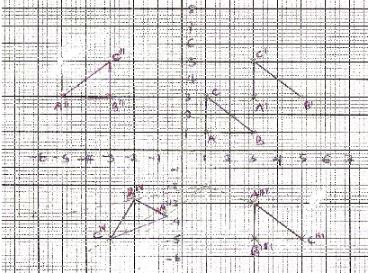
20. The coordinates of a triangle ABC are A(1, 1) B(3, 1) and C (1, 3).
    1. Plot the triangle ABC. (1 mark)
    2. Triangle ABC undergoes a translation vector (2  2) . Obtain the image of A' B' C ' under the transformation, write the coordinates of A' B' C'. (2 marks)
    3. A' B' C' undergoes a reflection along the line X = 0, obtain the coordinates and plot on the graph points A" B" C", under the transformation. (2 marks)
    4. The triangle A" B" C" , undergoes an enlargement scale factor -1, centre origin. Obtain the coordinates of the image A'" B"' C"'. (2 marks)
    5. The triangle A"' B"' C"' undergoes a rotation centre (1, -2) angle 120º. Obtain the coordinates of the image A^iv B^iv C^iv. 2 marks
    6. Which triangles are directly congruent. (1 mark)
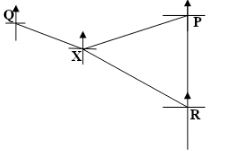
21. Three warships P, Q and R leave port X at 9:00am, ship P sails at a steady speed on a bearing of 070⁰, 100km from port X, while ship Q sails on a bearing of 320⁰, 80km from X. Ship R is on a bearing of 150⁰ from port X and due south of ship P.
    1. Use scale drawing to show the position of P,Q,R and X (4marks)
    2. Use the scale drawing to determine
       1. The distance and bearing of ship P from ship Q (2 marks)
       2. The distance of ship R from port X (2 marks)
       3. The distance of ship R from ship P (2 marks)
22. A rectangular tank whose internal dimensions are 2.04m by 1.68m by 26.4 m is ⁷/₈ full of milk
    1. If the tank is made of metal of thickness 3mm. Calculate the external volume of the tank in m³ when closed. (3 marks)
    2. Calculate the volume of milk in the tank in cubic metres. (2 marks)
    3. The milk is to be packed in small packets. Each packet is in the shape of a Right - Pyramid on an equilateral triangular base of side 19.2cm. The height of each packet is 13.6 cm. Full packets obtained are sold at kshs. 35 per packet. Calculate;
       1. The volume of milk, in cubic centimeters contained in each packet to 4 significance figures. Hence find the number of full packets. (3 marks)
       2. The exact amount that will be realized from the sale of all the packets of milk.(2 marks)
23.              
    1. Find the inverse of the matrix (2marks)
       
    2. A transport company has two types of vehicles for hire: Lorries and buses. The vehicles are hired per day. The cost of hiring two lorries and five buses is Sh. 156,000 and that of hiring 4 lorries and three buses is Sh. 137,000.
       1. Form two equations to represent the above information. (2 marks)
       2. Use matrix method to determine the cost of hiring a lorry and that of hiring a bus. (3 marks)
    3. Find the value of x given a singular matrix (3 marks)
       
24.                     
    1.            
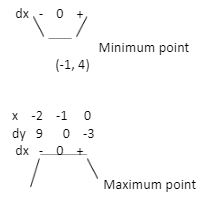
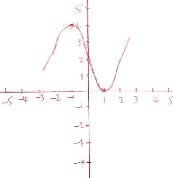
       1. Find the co-ordinates of the stationary points of the curve y = x³ – 3x + 2. (4 marks)
       2. For each stationary point determine its nature (2 marks)
    2. Determine the y-intercept (2 marks)
    3. In the space provided sketch the graph of the function y = x³ – 3x + 2 (2 marks)

MARKING SCHEME

1.          
   1. 94344 – 36425 ÷ 5
      = 94344 – 7285
      = 87059
      
      
   2. 7000
      
      
2. Rhino - 15
   Zebras – ¾
   ¹/₅ + ³/₄=⁴⁺¹⁵/₂₀
   = ¹⁹/₂₀
   Zebras
   ²/₃ x ¹/₂₀ = ¹/₃₀
   ¹/₅ + ³/₄ + ¹/₃₀ =^12+45+2/₆₀
   = ⁵⁹/₆₀
   Fraction of warthogs is ¹/₆₀
   
   
3. Length of the cube ³√2744
   = 14cm
   Diagonal of a face
   = √392
   = √196 x 2
   = 14√2cm
   
   
4. (3³)^²/₃ x (16/81)^³/₄
   9 × (^2⁴/_3⁴)^³/₄
   9× (²/₃)³
   9× (⁸/₂₇)
   ⁸/₃=2 ²/₃
   
   
5.      
      
   BC=5.8CM
   
   
6. Mass of the liquid
   Density = ^Mass/_Volume
   1.2 = ^m/₃₀₀
   = 360gm
   Total mass = 360 + 380
   = 640gm
   
   
7.      
   
   Completed cuboid
   Use of dotted lines for the hidden edges
   
   
8. 2p = p (1 + ^r/₂₀₀)¹⁰
   = 1+ ^r/₂₀₀
   1.0718 = 1+^r/₂₀₀
   0.0718 = ^r/₂₀₀
   r = 0.0718 x 200
   = 14.36%
   
   
9.              
   1. (2n – 4)90 = 40 (³⁶⁰/_n)
      2.25n(2n – 4) = 360
      4.5n² – 9n – 360 = 0
      n²- 2n – 80 = 0
      n² – 10n + 8n – 80 = 0
      n(n-10) + 8(n – 10) = 0
      ∴ n = 10
      
      
   2. Decagon
10.                     
    1. Class
       

       (a – b)	f	x = (a+b/2)	fx
       38 – 39 40-41 42-43 44-45 46-47 48-49	3 7 7 5 6 4	38.5 40.5 42.5 44.5 46.5 48.5	115.5 283.5 297.5 222.5 279 194
       	Σ=32		Σfx=1392
       	B1		B1

    2. x = ¹³⁹²/₃₂
       = 43.5
11.          
    1. q = 5 (-2  -3) - 3(1  -2)
       = (-10 -3 -15 + 6)
       = (-13   -9)
       
       
    2. Translation
       (3    2) (-0    -2)
       = (3     4)
       
       
12. 5(-5)² - (2x-3) - (4x-¹/₃)
          ¹/₃(-3)²+2x-5
    = 125 - 6 + ⁴/₃
         ¹/₃(9-10)
    = 120¹/₃
       ^-1/₃
    = ³⁶¹/₃ x ^-3/₁
    = -361
13.        
    Cos 30º = ^√3/₂
    ⇒(3x - 180º) = 30º, 330º
    ⇒3x= 30º + 180º, 30º + 180º
    x = ^210º/₃  , ^510º/₃
    x=70º, 170º
    
    
14. numerator : (2t + 5a) (2t – 5a)
    denominator:3(2t + 5a) (t - a)
      (2t + 5a)(2t – 5a)  
    3(2t + 5a)(t - a)
      2t – 5a  
      3t – 3a
    accept
      2t – 5a  
      3(t – a)
15.          
    1.   20-0     m/s
        10-0
       = 2m/s²
       
       
    2. ½ x 10 x 20 + ½ x 5 (20 + 15)+5 x 15 + ½ x 10 x 15
       
       
    3. = 100 + 87.5 + 75 + 75
       = 337.5m
       
       
16. 840 = 2³ × 3 × 5 × 7
    396= 2² x 3² × 11
    G.C.D = 2² x 3²=12
    Area = 12 ×12=144
    
    
17.            
    1. Amount received = 12000 x 240
       = KSh. 2,888,000
       
       
    2.            
       1. Sales = 125100 x 12000 x 240
          = 3,600,000
          Decreased 90100x 360,000 = 3,240,000
          % increase =
          3,240,000 - 2,880,000  x 100
             2,880,000
          =   360000      x 100
              280000
          = 12.5%
          
          
       2. New price in 2003
          ¹⁶/₁₅ x ¹²⁵/₁₀₀ x 12000
          KSh. 16000
          
          
    3. No. of sofa sets sold in the year 2003
       90/100 x 240=216
       No. of sets sold in the year2003 =
       Sales in year 2003   = 3240000 
       Price per sofa set         16000
       = 203
       P = 216 - 202.5  x 100
                216
       P = 6.25%
18.         
    1. L ⇒ (-2, 3) (-1,6)
       Gradient =
         6-3     =      3   =   3  =3
       -1- -2         -1+2      1
          y-3   = 3
         x- -2
          y-3   =31
         x+2
       y – 3 = 3x + 6
       y = 3x + 6 + 3
       y = 3x + 9
       
       
    2. P ⇒m₁xm₂ = -1
       3m₂ = -1
       m₂ = ^-1/₃
         y-6  = -13
       x- -1
          y-6  = -13
         x+ 1
       3(y – 6) = -x - 1
       3y – 18 = -x - 1
       3y = -x + 17
       x + 3y = 17
       
       
    3. Q ⇒ m₁ = m₂ = 3 (1,2)
         y-2     =  3  
         x-1         1
       y – 2 = 3x – 3
       y = 3x – 3 + 2
       y = 3x – 1
       At y – intercept, x = 0
       y = 3x – 1
       y = 3(0) – 1
       y = -1
       y – intercept (0,-1)
       At x – intercept, y = 0
       y = 3x – 1
       0 = 3x – 1
       ^3x/₃=¹/₃
       x = ¹/₃
       x – intercept (13,0)
       
       
    4. Point of intersection
       P ⇒ x + 3y = 17 y = -1 –x3+173 ……………(1)
       Q ⇒ y = 3x – 1 ……….. (ii)
       Equating (i) and (ii)
       3x – 1 = ^-x/₃ + ¹⁷/₃
       3x + ^x/₃= ¹⁷/₃ + 1
       ⇒ ¹⁰/₃ x=²⁰/₃
       x = ²⁰/₃ x ³/₁₀
       x = 2
       
       
    5. x = 2
       y = 3x – 1
       y = 3(2) – 1
       y = 6 -1
       y = 5
       x = 2
       y = 5
       P (2,5)
       
       
19.                 
    1. a² = b² + c² – 2bcCos A
       a² = 6² + 8² – 2 x 6 x Cos 50
       a² = 36 + 64 – 61.71
       a² = 100 – 61.71
       a = 6.188cm
       B = 6.19cm
       
       
    2. ^a/_{Sin A}= ^b/_{Sin B} = ^c/_{Sin C}
       ^6.188/_{Sin 50}=⁶/_{Sin B}
       Sin B = ^{6 Sin 50}/_6.188
       B = 47.97º
       
       
    3. a² = d² + c² – 2dCos A
       2.82² = 6² + 7² – 2 x 6 x 7 x Cos A
       7.9524 = 36 + 49 – 84Cos A
       7.9524 = 85 – 84Cos A
       84Cos A = 85 – 7.9524
       Cos A = ^77.0476/₈₄
       A = 23.480
       
       
    4. Area of Δ ACD
       A = ½ ab sin C
       A = ½ x 7 x 6 c Sin 23.48
       A = 21 Sin 23.48
       A = 8.367cm²
       A = 8.37cm
20.                  
    1.            
        
    2. A¹ = (1 1) + (2 2) = (3 3)      
       B¹ = (3 1) + (2 2) = (5 3)
       C¹ = (1 3) + (2 2) = (3 5)
       A¹(3,3) B¹(5,3)C¹(3,5)
       
       
    3. A¹¹ = -5,3
       B11 = (-3, 3)
       C11 = (-3,5)
       
       
    4. A111 = 3,-3
       B111 = (5, -3)
       C111 = (3,-5)
       
       
    5. A1V(-0.8,-3.8)
       BIV = (-2, -2.8)
       CIV = (-3,-5)
       
       
    6. direct congruent ABC and A¹ B¹ C¹
21.                  
    1.    
       
    2.        
       1. the distance and bearing of ship P from ship Q Distance = 148km ± 2km
          Bearing = 102º ± 1º
       2. the distance of ship R from port X = 196km ± 2km
       3. the distance of ship R from ship P
          = 204 ± 2km
          Allow S78ºE
22.          
    1. External volume
       = 2.046 x 1.686 x 2.646 = 9.12 m³
       
       
    2. 1.68 x 2.04 x 2.64 m³
       = 9.047808 m³
    3.        
       1. Vol of packet = ½ 192.2 x sin 60º x 13.6
          = 2,171 cm³
          Number of packets = ^9047808/₂₁₇₁
          = 4,167✓
       2. 4,167 x 35 = shs. 145,845✓
23.           
    1. 
       Determinant = (2 x 3) – ( 4 x 5)
       = 6 – 20 = -14
       Inverse = 
       
       Let L be the cost of hiring a lorry and Sh. b be that of hiring a bus
    2.          
       1. 2L + 5b = 156000
          4L + 3b = 137000
       2. 
          
    3. A singular matrix has a determinant = 0
       [2x -1 1 x² 1]
       (2x – 1) – x2 = 0
       2x – 1 – x2 = 0
       x² – 2x + 1 = 0
       p = 1
       s = -2
       f = -1, -1
       (x2 – x) – (x + 1) = 0
       x(x-1) -1 (x -1) = 0
       x = 1
24.                  
    1.            
       1. Stationary points of y = x3 – 3x + 2
          ^dy/_dx=3x² - 3
          y = x³ – 3x + 2
          At stationary points ^dy/_dx=0
          ∴ 3x² – 3 = 0
          ^3x²/₃=³/₃
          x² = 1
          x = ± 1
          When x = 1
          y = 1³ – 3(-1) + 2
          y = 1 – 3 + + 2
          y = 0
          (1,0)
          When x = -1
          y = (-1)³ – 3(-1) + 2
          y = -1 + 3 + 2
          y = 4
          (-1,4)
       2. Nature of the stationary points
          (1,0) dy/dx=3x2- 3
          x   0  1 2
          dy -3 0 9
          
    2. y – Intercept, x = 0
       y = x³ – 3x + 2
       y = 03 – 3(0) + 2
       y = 2
       (0,2)
    3.