MATHEMATICS
PAPER 2
INSTRUCTIONS TO CANDIDATES
- Write your name, index number and class in the spaces provided above.
- The paper contains two sections: Section I and Section II.
- Answer ALL the questions in Section I and ANY FIVE questions from Section II.
- All working and answers must be written on the question paper in the spaces provided below each question.
- Marks may be awarded for correct working even if the answer is wrong.
- Negligent and slovenly work will be penalized.
- Non-programmable silent electronic calculators and mathematical tables are allowed for use.
SECTION I (50 MARKS)
Answer ALL the questions in this section.
- Use logarithms to evaluate:(4 marks)
-
- Expand (1- 1/2x)6 up to fourth term. (2 marks)
- Use the expansion above to evaluate (0.98)6 (2 marks)
- The data below represents the ages in months at which 11 babies started walking:
9,15 , 12, 9, 8, 13, 7, 11, 13, 14 and 10.
Calculate the interquartile range of the above data (3 marks) - The fifth term of an arithmetic progression is 11 and the twenty fifth term is 51.
Calculate the first term and the common difference of the progression. (3 marks) - Find the values of a, b and c.(3 marks)
√3-2√2 = a√b+c
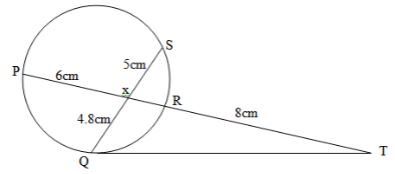
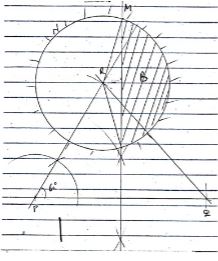
3√2+3 - In the figure below QT is a tangent to the circle at Q. PXRT and QXS are straight lines. PX = 6cm, RT = 8cm, QX = 4.8cm and XS = 5cm.
Find the length of QT (3 marks) - Solve for x in the equation below:
Log 3(x + 3) = 3 log 3 + 2 (3 marks) - Pipe A can fill a tank in 2 hours, Pipe B and C can empty the tank in 5 hours and 6 hours respectively. How long would it take:
- To fill the tank if A and B are left open and C is closed. (2 marks)
- To fill the tank with all pipes open. (2 marks)
- A transformation is represented by the matrix
. This transformation maps a triangle ABC of the area 12.5cm2 onto another triangle A′B′C′. Find the area of triangle A′B′C′. (3marks)
- Make P the subject of the formula XYP = QPX (3 marks)
- The coordinates of the end points of diameter are A(2,4) B(−2,6). Find the equation of a circle in the form
ax2 + by2 +cx + dy + e = 0 (3 marks) - A bag contains 10 balls of which 3 are red, 5 are white and 2 green. Another bag contains 12 balls of which 4 are red, 3 are white and 5 are green. A bag is chosen at random and a ball picked at random. Find the probability the ball so chosen is red. (3 marks)
- Use the trapezium rule with seven ordinates to find the area bounded by the curve y= x2+1 lines x = -2, x = 4 and x – axis (3 marks)
- Wanjiku pays for a car on hire purchase in 15 monthly instalments. The cash price of the car is Ksh.300, 000 and the interest rate is 15%p.a. A deposit of Ksh.75, 000 is made. Calculate her monthly repayments. (3 marks)
- The length and breadth of a rectangular floor garden were measured and found to be 4.1m and 2.2m respectively. Find the percentage error in its area. (3 marks)
- The gradient function of a curve is given dy/dx = 3x2 – 8x + 2. If the curve passes through the point, (2, –2), find its equation. (3 marks)
SECTION II (50 MARKS)
Answer five questions only from this section
- The following table shows the rate at which income tax was charged during a certain year.
A civil servant earns a basic salary of Ksh.35750 and a monthly house allowance of sh.12500. The civil servant is entitled to a personal relief of sh.1062 per month. Calculate:Monthly taxable income in Ksh. Tax rate % 0 - 9860
9861 - 19720
19721 - 29580
29581 - 39440
39441 - 49300
49301 - 59160
over 5916010
15
20
25
30
35
40- Taxable income (2 marks)
- Calculate his net monthly tax (5 marks)
- Apart from the salary the following deduction are also made from his monthly income.
WCPS at 2% of the basic salary
Loan repayment Ksh.1325
NHIF sh.480
Calculate his net monthly earning. (3 marks)
-
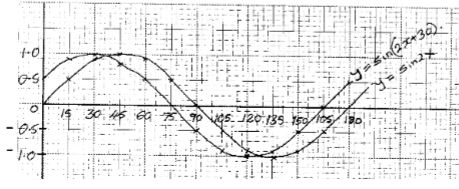
- Complete the table below for y=sin 2x and y=sin ( 2x + 30) giving values to 2d.p
(2 marks)x 0 15 30 45 60 75 90 105 120 135 150 165 180 Sin 2x 0 0.87 -0.87 0 Sin(2x +30) 0.5 0.5 -1 0.5 - Draw the graphs of y=sin 2x and y = sin (2x + 30) on the axis. (4 marks)
- Use the graph to solve (1 mark)
Sin (2x + 30) - Sin 2x =0 - Determine the transformation which maps Sin 2x onto Sin (2x + 30) (1 mark)
- State the period and amplitude of y=Sin(2x +30) (2 marks)
- Complete the table below for y=sin 2x and y=sin ( 2x + 30) giving values to 2d.p
- A plane S flies from a point P (400N, 450W) to a point Q (350N, 450W) and then to another point T (350N, 1350E).
- Given that the radius of the earth is 6370km find the distance from P to Q in Km.
(Take π = 22/7) (2 marks) - Find in nm
- The shortest distance between Q and T. (2 marks)
- The longest distance between Q and T (to the nearest tens) (2 marks)
- Find the difference in time taken when S flies along the shortest and longest routes if its speed is 420 knots (4 marks)
- Given that the radius of the earth is 6370km find the distance from P to Q in Km.
- The following table shows the distribution of marks obtained by 50 students.
By using an assumed mean of 62, calculateMarks 45 – 49 50-54 55-59 60-64 65-69 70-74 75-79 No. of students 3 9 13 15 5 4 1 - the mean (5 marks)
- the variance (3 marks)
- the standard deviation (2 marks) `
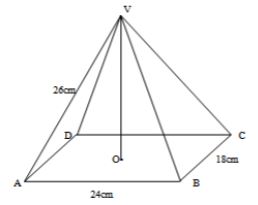
- The diagram below represents a pyramid standing on rectangular base ABCO. V is the vertex of the pyramid and VA = VB = VC = VD = 26 cm. M is the midpoints of BC and AC respectively. AB = 24 cm and BC = 18 cm.
Calculate:-- The length of the projection of line VA on plane ABCD (2marks)
- The angle between line VA and the plane ABCD. (2marks)
- The size of the angle between the planes VBC and ABCD. (2marks)
- The vertical height of the pyramid. (2marks)
- The volume of the pyramid (2marks)
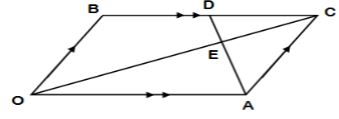
- A parallelogram OACB is such that OA = a, OB = b. D is the mid-point of BC. OE = hOC and AE = kAD.
- Express the following in terms of a, b, h and k.
- OC (1 mark)
- OE (1 mark)
- AD (1 mark)
- AE (1 mark)
- Find the values of h and k. (4 marks)
- Determine the ratios:
- AE : ED (1 mark)
- OE : OC (1 mark)
- Express the following in terms of a, b, h and k.
- A uniform distributor is required to supply two sizes of skirts to a school: medium and large sizes. She was given the following conditions by the school.
- The total number of skirts must not exceed 600.
- The number of medium size skirts must be more than the number of large size skirts.
- The number of medium size skirts must not be more than 350 and the number of large size skirts must not be less than 150. If the distributor supplied χ medium size and y large size skirts.
- Write down, in terms of χ and y, all the linear inequalities representing the conditions above. (4mks)
- On the grid provided, represent the inequalities in (a) above by shading the unwanted regions. (4mks)
- The distributor made the following profits per skirt.: Medium size = Sh.300., Large size = Sh.250. Determine the maximum profit. (3mks)
-
- On the same diagram construct:-
- Triangle PQR such that PQ = 9cm, PR = 7cm and triangle RPQ = 600 (2 marks)
- The locus of a point M such that M is equidistant from P and Q. (1mark)
- The locus of a point N such that RN ≤ 3.5cm. (1 mark)
- On the diagram in part (a)
- Shade the region B, containing all the points enclosed by the locus on M and the locus of N such that PM ≥ QM. (2marks)
- Find the area of the shaded region in (i) above (4marks)
- On the same diagram construct:-
MARKING SCHEME
-
No Std form Log 45.3
0.00697
0.534
0.83924.5×101
6.97×10-3
5.34×10-1
8.392×10-11.6561
3.8432 +
1.4993
1.7275-
1.7718÷3
1.92390.8392 -
- 16 + 6.15(-1/2x)+15.14(-1/2x)2 +20.13(-1/2x)3
=1 - 3x + 15/4x2 - 5/4x3 - -1/2x= -0.02
x= 0.04
= 1 - 30.04+15/4(0.04)2+5/4(0.04)3
= 1.11392
- 16 + 6.15(-1/2x)+15.14(-1/2x)2 +20.13(-1/2x)3
- Arrange in ascending order
7,8,9,9,10,11,12,13,13,14,15
Q1 = 9
Q3 = 13
Quartile range = 13 – 9 = 4 - a + 4d = 11 (i)
a + 24d = 51 ii
20d=40
d = 2 a = 3 - √3-2√2 x 3√2- √3
3√2+ √3 3√2- √3
3√6-12+2√6
18-3
1/3√6-1
a=1/3,b=6 and c=-1 - X R = 4.8 × 5/6=4
QT2 = PT x RT
QT 2 = 18 x 8
QT = √144
QT = 12cm - log (3x + 9) = log 33 + log 100
log (3x + 9) = log 2700
3x + 9 = 2700
3x = 2691
3x = 2691
3 3
x = 897 -
- 1/2 - 1/5= 3/10
Required time = 10/3
= 3 1/3 or 3 hours 20 mins - 1/2 - 1/5 - 1/6= 4/30
Required time = 30/3
= 7 hrs. 30mins or 7 ½
- 1/2 - 1/5= 3/10
- Determinant = 2 – 12 = –10
A.S.F= -10
= 10
10x 12.5 = 125 cm2 - Log x+p=px
Log x + p log y=px log Q
Log x=px log Q- p log y
Log x= p(x log Q-log y)
log x = p
xlog Q - log y - Midpoint (2+-2/2,4+6/2)
0,5
Length= √(0-2)2(5-4)2
Radius √4+1 =5units
(x-0)2+ (y-5)2 =√52
X2 + y2 - 10y + 20=0 - P(R) bag A 1/2 x 4/12= 1/6
P(R) bag B 1/2 x 3/10= 3/20
1/6 + 3/10 =38/120
= 19/60
Area = 1/2 ( 5 + 17 + 2(2 + 1 + 2 + 5 + 10)x -2 -1 0 1 2 3 4 y 5 2 1 2 5 10 17
= 31 sq. Units- P = 300,000 - 75000 = 225,000
A = 225,000 x 1.151.25
= 225,000 x 1.151.25
15
225000 x 1.190 = 267950
15 15
= Ksh.17863 - Maximum area 4015 x 2.25=9.3375
Actual area 4.1 x 2.2=9.02
Minimum area 4.05 x 2.15 = 8.7075
A.e = 9.3375-8.7075
2
= 0.315
%error=0.315/9.02 × 100%
= 3.492% - dy/dx = 3x2-8x+2
y = x3-4x2+2x+c
At x = 2 y=-2
- 2 = 8-16+4+c
C=2
y = x3- 4x2 + 2x+2 -
- taxable income
- 35750 + 12500 = 48250= sh.48250
- 35750 + 12500 = 48250= sh.48250
- 9860 x 10/100 = 986
9860 x 75/100 = 1479
9860 x 20/100 = 2976
9860 x 25/100 = 2465
8810 x 30/100 = 2643
9545
Total less relief 1062
sh.8483pm - WCPS = 2/100 x 35750 = 715
Total deduction
(8483 + 715 + 1325 + 480) = 11000
Net salary = 48250 - 11000
sh.37250 p.m
- taxable income
-
-
X 0 15 30 45 60 75 90 105 120 135 150 160 180 Sin 2x 0 0.5 0.87 1 0.87 0.5 0 -0.5 -0.87 -1 -0.87 -0.5 0 Sin (2x +30) 0.5 0.87 1 0.87 0.5 0 -0.5 -0.87 -1 -0.87 0.5 0 0.5 -
- x = 30.6o 120.9o
- Translation
- Period 180o amplitude 1
-
-
- 10/360 x 2 x 22/7 x 6370
= 1112km -
- 110 x 60
= 6600nm - 180 x 60 x cos 35º
= 8850nm.
- 110 x 60
- 420 = 6600
T1 = 6600
420
= 15hr 43min
420 = 8850
T2
T2 = 21h 4min
T2 – T1 = 21hr 4min – 15hr 43min
= 5hrs 21min
- 10/360 x 2 x 22/7 x 6370
-
- A =62
Marks f x d=x-A Fd d2 Fd2 45 – 49
50 -54
55- 59
60 – 64
65 – 69
70 – 74
75- 793
9
13
15
5
4
147
52
57
62
67
72
77-15
-10
-5
0
5
10
15-45
-90
-65
0
25
40
15225
100
25
0
25
100
225675
900
325
0
125
400
225f=50 Σfd=120 Σfd2=2650
Mean , x = A + ∑fd
∑f
= 62 + -120/50
= 62 - 2.4
= 59.6 - v = ∑fd2 - (∑fd/ ∑f )2
∑f
= 2650 - (120/50)2
50
= 53 – 5.7 = 47 .24 - s.d = √ ∑fd2 - (∑fd/ ∑f )2
∑f
=√ 47.24
= 6.873
- A =62
- C=182+242
=30 cm
VA = 0.5×30=15 cm - cos θ=1526
θ=54.77 - ϑ=21.2412 =60.54°
√262-15
=21.24 cm - v=13Ah=13×24×18×21.24
=3058.56 cm3
- C=182+242
-
-
- →
Oc= a + b
→ - OE= h (a + b)
→ - AD = b – ½ a
→ - AE = k (b – ½ a)
- →
- →
OE = a + k (b – ½ a)
a + kb – ½ ka = ha + hb
(1 – ½ k) = h
K – h
1 – ½ h = h
1 = 3/2h
h = 2/3 k = 2/3 - →
AE = 2/3AD
AE : ED
2 : 1
OE : OC
OE = 2/3OC
= 2 :1
-
- x+y≤600
x>y
x≤350
y≥150
300x+250y
300350+250250=sh167500 -
A = 147/360 × 22/7 × 3.5×3.5 – ½ × 3.5×3.5sin147
= 1.2 384 cm2
Download Mathematics Paper 2 Questions and Answers - MECS Cluster Joint Mock Exams 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students