INSTRUCTIONS TO CANDIDATES
- Write your name, stream, admission number and index number in the spaces provided above.
- The paper contains two sections, Section I and II
- Answer all questions in section I and ONLY any FIVE questions from section II.
- All answers and working must be shown on the question paper in the spaces below each question
- Show all steps in your calculations, giving answers at each stage
- Marks may be given for each correct working even if the answer is wrong
- Non-programmable silent electronic calculators and KNEC mathematical tables may be used.
SECTION I (50 MARKS)
Answer all questions in this Section
- Evaluate : (3 mks)
- Simplify completely (3 mks)
12x2 - 11xy + 2y2
8x3 - 8xy2 - Use the exchange rates below to answer this question.
Buying Selling
1 US dollar 63.00 63.20
1 UK £ 125.30 125.95
Abwanja, a tourist arriving in Kenya from Britain had 9600 UK Sterling pounds (£). He converted the pounds to Kenya shillings at a commission of 5%. While in Kenya, he spent ¾ of this money. He changed the balance to US dollars after his stay. If he was not charged any commission for this last transaction, calculate to the nearest US dollars, the amount he received. (3 mks) - Solve for x in the following equation. (3mks)
4x(8x - 1) = tan 45º - The sum of interior angles of two regular polygons of sides; n and n + 2 are in the ratio 3:4. Calculate the sum of the interior angles of the polygon with n sides. (3mks)
- Use logarithms to evaluate the following correct to 4 decimal places.
4√2 x 1.764-2 x 0.324
5.42 (3mks) - By shading, show the region defined by the following linear inequalities (3mks)
2y < x + 4; 4y ≥ -x – 4; x ≤ 2
- Find the equation of locus of points equidistant from points A (6, 5) and B (-2, 3) in the form y = mx + c (3mks)
- The GCD of three numbers is 6 and their LCM is 900. If two of the numbers are 36 and 60, find the least possible third number.(3mks)
- Use the tables of squares, cube roots and reciprocals to evaluate (3mks)
3√0.008 - 10
0.375 37.52 - Solve the following pair of simultaneous equations using substitution method (3mks)
4x + 3y - 475 = 0
2x + 5y - 325 = 0 - Given that Sinθ = 0.8 and θ is an acute angle, find without using tables or calculators
- Tanθ (2mks)
- Cos (180 - θ) (1mk)
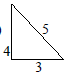
- The figure below is a triangular prism of uniform cross-section in which AF = FB =3cm,
AB = 4cm and BC = 5cm. Draw a clearly labeled net of the prism. (3mks)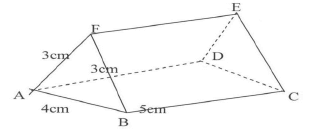
- The mass of two similar cans is 960g and 15000g. If the total surface area of the smaller can is 144cm2, determine the surface area of the larger can. (3mks)
- In the circle below, O is the centre, angle DAB = 87º , minor Arc AB is twice minor arc AD. CD is a tangent to the circle at D.
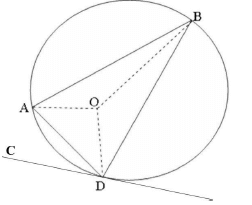
Giving reasons, Calculate the size of;- Angle AOB. (2mks)
- Angle ADT (2mks)
- A sector of a circle of radius 42cm subtends an angle of at the centre of the circle. The sector is folded into an inverted right cone. Calculate
- The radius of the cone (3mks)
- To one decimal place the vertical height of the cone (1mk)
SECTION II: 50 MARKS
Answer any FIVE questions in this section
- A bus and a Nissan left Nairobi for Eldoret, a distance of 340 km at 7.00 a.m. The bus travelled at 100km/h while the Nissan travelled at 120km/h. After 30 minutes, the Nissan had a puncture which took 30 minutes to mend.
- Find how far from Nairobi did the Nissan caught up with the bus (5mks)
- At what time of the day did the Nissan catch up with the bus? (2mks)
- Find the time at which the bus reached Eldoret (3mks)
- In the diagram below OA = a, OB = b the points P and Q are such that AP = 2/3 AB, OQ = 1/3 OA
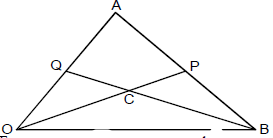
- Express OP and BQ in terms of a and b (2 mks)
- If OC = hOP and BC = kBQ, Express OC in two different way and hence
- Deduce the value of h and k. (5 mks)
- Express vector OC in terms of a and b only. (2 mks)
- State the ratio in which C divides BQ (1 mk)
- The table below shows the marks scored in a Mathematics examination.
- Calculate the mean mark (3mks)
Marks Frequency 5 – 14 2 15 – 34 22 35 – 54 50 55 – 84 24 85 – 94 2 - Draw a histogram to represent the above information (4mks)
- Using the histogram, find the median mark (3mks)
- Calculate the mean mark (3mks)
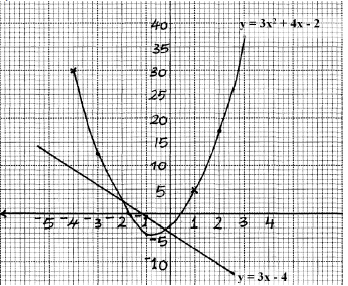
- Given the quadratic function y = 3x2 + 4x - 2
- Complete the table below for values of x ranging - 4 ≤ x ≤ 3. (2mks)
x -4 -3 -2 -1 0 1 2 3 y - Using the grid provided draw the graph of y = 3x2 + 4x – 2 for -4 ≤ x ≤ 3 (3mks)
- Using the graph, find the solution to the equations.
- 3x2 + 4x – 2 = 0 (2mks)
- 3x2 + 7x + 2 = 0 (3mks)
- Complete the table below for values of x ranging - 4 ≤ x ≤ 3. (2mks)
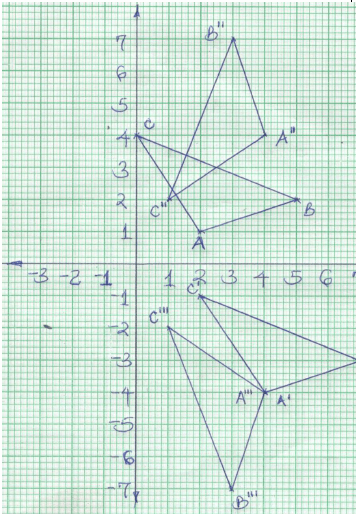
- A triangle ABC has vertices A(2,1), B(5,2) and C(0,4).
- On the grid provided plot the triangle ABC. (2 mks)
- A1B1C1 is the image of ABC under a translation(2-5) . Plot A1B1C1 and state its coordinates. (2mks)
- Plot A11B11C11 the image of A1B1C1 under a rotation about the origin through a negative quarter turn. State its coordinates. (3 mks)
- A111B111C111 is the image of A11B11C11 under a reflection on the line y = 0. Plot A111B111C111 and state its coordinates. (3 mks)
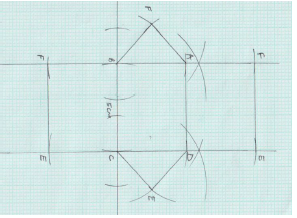
- Two Airstrips P and Q are such that Q is 500km due East of P. Two warplanes M and N
Leave from P and Q respectively at the same time. Warplane M moves at 360km/h on a bearing of 030º. Warplane N moves at a speed of 240km/h on a bearing of 315º. The two warplanes landed at Police camps A and B respectively after 90 minutes. Using a scale of 1cm represent 100km- Show the relative positions of the two police camps A and B (6mks)
- Find the shortest distance between the police camps A and B. (2mks)
- Find the true bearing of;
- Police camp A from B (1mk)
- Police camp B from A (1mk)
- The diagram below represents square based pyramid standing vertically. AB = 12cm, PQ = 4cm and the height of pyramid PQSV is 10cm.
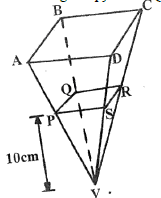
- If PQRSV is a solid, find the volume of material used to make it. (2mks)
- Find the
- height of the frustum ABCDPQRS (2mks)
- Volume of the frustum (3mks)
- The liquid from a hemisphere is poured into PQRS. Find radius correct to 4 significant figures of the hemisphere if the liquid from hemisphere filled the solid completely. Use π = 22/7 (3mks)
- The displacement h metres of a particle moving along a straight line after t seconds is given by h = -2t3 + 3/2 t2 + 3t
- Find the initial acceleration. (3mks)
- Calculate
- The time when the particle was momentarily at rest. (3mks)
- Its displacement by the time it comes to rest momentarily. (2mks)
- Calculate the maximum speed attained. (2mks)

MARKING SCHEME
- Numerator: 7/9 + 2/18 = 8/9
Denominator:2/5 x 10/3 x 3/1 = 4
8/9 x ¼ = 2/9 - N;(3x - 2y)(4x - y)
D;2x(3x - 2y)(3x + 2y)
(3x - 2y)(4y - y)
2x(3x - 2y)(3x + 2y)
4x - y
2x(3x - 2y) - UK £6900 = sh125.30 x 9600
= sh 1 202 880
95/10 x 1 202 880 = sh1 142 736
¼ x 1 142 736 = 285 684
285 684 = 4520.32
63.20
= $4520 - 4x(8x-1) = 1
8x-1 = 1
4x
23(x - 1) = 1
22x
23x - 3 = 2-2x
3x - 3 = -2x
x = 3/5 - 90(2n - 4) = 3
90º (2n) 4
(2n - 4) = 3
2n 4
8n - 16 = 6n
n = 8
90º(2 x 8 -4)
1080º -
No. Log 2
0.324
0.3010
-
1.5105
1.81151.7642
5.42
0.44280.2465 x 2
0.4930 -
0.7340 +
1.2270
2.5845 x ¼
- 4+ 2.5845
4
1.6462 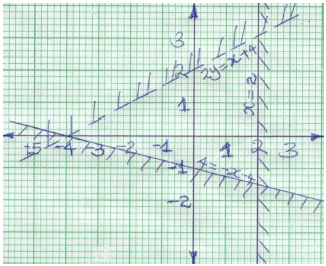
2y<x +4
4y ≥ - x- 4
x≤2- Midpoint (6+-2, 5 + 3)
2 2
(2,4)
m1 = 3 - 5 = ¼
-2 -6
m2 = -4
y - 4 = -4
x - 2
y = -4x + 12 - GCD = 6 = 2 x 3
LCM = 900 = 22 x 32 x 52
36 = 22 x 32
60 = 22 x 3 x 5
Least possible number = 2 x 3 x 52 = 150 - 0.2 x 10 x 1 - 10 x 1 x 1
3.75 1.406 1000
.0.2 x 10 0.2667 - 10 x 0.7114 x 0.001
0.5334 - 0.007114
0.526286 - 4x + 3y = 475
5y + 2x = 325
x =325 - 5y
2
4(325 - 5y ) + 3y = 475
2
-7y = -175
7y = 175
y = 25
x =325 - 5(25)
2
x = 100 -
Tanθ = 4/3- Cos(180 - θ) = -3/5
Complete net, well labelled- V.s.f = 960:1500
= 8:236
L.s.f = 2:5
A.s.f= 4:25
Surface area of the larger can = 144 x 25
4
= 900cm2 -
- Let <AOD = y <AOB = 2y
<BOD = 2 <DAB = 2 x 87 = 174º
y + 2y + 174 = 360º
<AOB = 2 x 62 = 124º
sum of angle at a point add up to 360º - <ADT = <ABD = 28 + 3 = 31º
angles in alternate segment are equal
- Let <AOD = y <AOB = 2y
-
- θ x 2πR = 2πr
360
120 x 2 x π x 42 = 2πr
360
r =120 x 42
36
= 14cm - h = √422 - 142
= 39.6cm
- θ x 2πR = 2πr
-
- Distance after 30mins
Bus → 100 x ½ = 50km
Nissan → 120 x ½ = 60km
Distance covered by bus in 1hr
50 km + 50km = 100km
Relative distance = 100 - 60
= 40km
Relative speed = 120 - 100
= 20km/hr
= Time taken to catch up = 40/20
= 2hrs
Distance from Nrb = 60 + (120 x 2)
60 + 240 = 300km - 7.00am + 1hr + 2hrs
= 10.00am - time =340 = 3.4hrs → 3hrs 24mins
100
Arrive time = 7.00am + 3hrs 24mins
= 10.24am
- Distance after 30mins
-
- OP = a + 2/3(b - a)
= 1/3a + 2/3b
BQ = 1/3a - b -
- OC = H(1/3a + 2/3b)
= 1/3ha + 2/3hb
OC = b + k (1/3a - b)
1/3ka + (1 - k)b
1/3h = 1/3k
h = k
2/3h = 1 - k
2/3k = 1 - k
2k = 3 - 3k
5k = 3
k = h = 3/5 - OC = (1/3)(3/5)a + (2/3)(3/5)b
= 1/5a + 2/5b - BC:CQ = 3/5:2/5
BC:CQ = 3:2
- OC = H(1/3a + 2/3b)
- OP = a + 2/3(b - a)
mean = ∑fx = 4630 = 46.3x fx fd 9.5 19 .0.2 24.5 539 1.1 44.5 2225 2.5 69.5 1668 0.8 89.5 179 0.2 ∑fx = 4630
∑f 100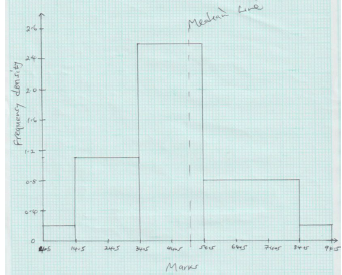
Total area = 2 + 22 + 50 + 24 + 2 = 100
50 – (2 + 22) = 26+26 = 2.5 x y, y = 10.4
Median = 34.5 + 10.4
= 44.9-
-
x -4 -3 -2 -1 0 1 2 3 y 30 13 2 -3 -2 5 18 37 -
-
- x = + 0.4
x = -1.7
±0.1 - y = 3x2 + 4x – 2
0 = 3x2 + 7x + 2
y = -3x – 4
x = -2 or x = -0.4 ± 0.1
For equation of line
For line drawn
- x = + 0.4
-
-
For plotting
For ΔABC
For ΔA1B1C1
For construction or otherwise
For ΔA11B11C11
For construction or otherwise
For ΔA111B111C111- A1(4,-4) B1(7,-3) C1(2,-1)
- A11(4,4) B11(3,7) C11(1,2)
- A111(4,-4) B111(3,-7) C111(1,-2)
-
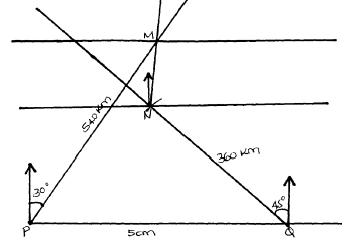
1cm rep.100km
<30º at P
<45º at Q
positions of PQM and N
labelling 540km, 360km, 500km all- 2.1 + 0.1cm
200km, 210km, 220km -
- Bearing of M from N = 010º ± 1º
- Bearing of N from M = 190º ± 1º
-
- 1/3 x 4 x 10 = 531/3 cm2
-
- 4.243 = 10 + H
2.828 10
42.43 = 28.28 + 2.828H
H = 14.15 = 5.004
2.828 - Volume of frustum
1/3 x 12 x 12 x 15.004 - 1/3 x 4 x 4 x 10
720.192 - 53.33
666.86cm3
- 4.243 = 10 + H
- 2/3 x 22/7 x r3 = 531/3
r3 =159 x 7 x 3
3 22 2
= 25.30
r = 935cm
-
- V = dh/dt = -6t2 + 3t + 3
a = dv/dt = -12t + 3
at t = 0,a = -12(0) + 3
3m/s2- -6t2 + 3t + 3 = 0 → 2t2 t - 1 = 0
2t(t - 1) + 1(t - 1) = 0
(2t + 1)(t - 1) = 0
t = 1 or -0.5
time = 1sec - h = -2(1)3 + 3/2(1)2 + 3(1)
= 2.5m
- -6t2 + 3t + 3 = 0 → 2t2 t - 1 = 0
- at maximum speed dv/dt = 0
-12t + 3 = 0
t = ¼
Maximum speed, -6(¼)2 + 3(¼) + 3
3.375m/s
- V = dh/dt = -6t2 + 3t + 3
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - Butere Mock Exams 2021.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

