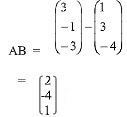Questions
INSTRUCTIONS:
- This paper consists of Two sections 1 and II.
- Answer all the questions in section 1 and only five questions from section II
- Show all the steps in your calculation, giving your answers at each stage in the space provided.
- Marks may be given for correct working even if the answer is wrong.
- Non programmable silent electronic calculator and KNEC Mathematical table may be used, except when stated otherwise.
SECTION 1 (50 MARKS) COMPULSORY
- Without using calculators evaluate: (3 marks)
½ ÷ 2 ⁴/₅ of 8 ÷ 6(2 x 4²/₅)
½ of 6 (8 ÷ 7¹/₃) - Simplify the expression (3 marks)
y⁴ - x⁴
y³ – yx² - Solve for x in the equation (3 marks)
2(2x-1) x (1/8) (1 – x) = 4(3x + 1) - The marked price of a modern camera is Ksh. 24,000. A trader sold it to a customer at a 10% discount. If the trader still made a profit of 20% on the cost price, what was its cost price. (3 marks)
- A two – digit number is such that the sum of the digit is 12. If the digits are interchanged the value of the new number formed is fifteen more than twice the value of the original number. Find the original number? (4 marks)
- Using reciprocal and square – root tables only. Evaluate. (3 marks)
9.4522 + 1/63.37 - Two similar container hold 2000cm3 and 6.75 litres respectively. If the smaller container has a diameter of 15.50cm. What is the radius of the larger container correct to 1 decimal place? (3 marks)
- Given that OA = i + 3j - 4k and OB = 3i - j - k. (3 marks)
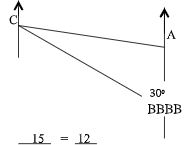
Find /AB/ - Three schools A, B, and C are such that B is 12km due south of A and C is 15km from A. C is on a bearing of N300W from B. Calculate the bearing of C from A. (3 marks)
- Solve the inequality
3 – 2 x ˂ x ≤ 2x + 5
3
State the integral values which satisfy these inequalities (3 marks) - The gradient of a line L through A (2x, 4) and B (-1, x) is 1/7. Find the equation of line perpendicular to L through B. (3 marks)
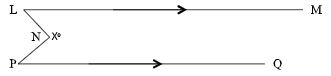
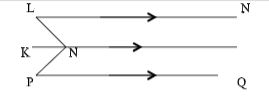
- On the figure below LM is parallel to PQ. Angle MLN = 300 and Angle NPQ = 700. Find the value of X0 (3 marks)
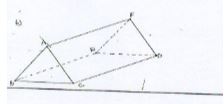
- Complete the sketch below for the prism, ABCDEF (3 marks)
- A Jua Kali artisan has 63000g of metal of density 7g/cm3. He intends to use it to make a rectangular pipe with external dimensions 120mm by 150mm and internal dimensions of 100mm by 120mm. Calculate the length of the pipe in metres. (3 marks)
- Jane and Mary started a business whereby contributed Ksh. 25000 and 20000 respectively. At the end of the year a profit of Ksh. 8100 was realized. From the profit funds for development, dividends and reserves were set aside in the ration 4:5:6 respectively. If the dividends were shared in the ration of their contribution, determine:
- The amount set aside for development (2 marks)
- The dividends Mary received (2 marks)
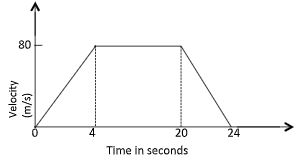
- The figure below is a velocity time - graph for car
- Find total distance traveled by the car (2 marks)
- Calculate the deceleration of the car. (1 mark)
SECTION II (50 MARKS)
Answer any five questions in this section
- Five members of a self-supporting enterprise Peter, John, Esther, Brian and Caro were given a certain amount of money to share amongst themselves. Peter got 3/8 of the total amount while John got 2/5 of the remainder. The remaining amount was shared equally among Esther, Brian and Caro each of which received Ksh. 6,000;
- How much was shared among the five business women? (3 marks)
- How much did John get? (2 marks)
- Peter, John and Caro invested their money and earned a profit of Ksh. 12,000. A third of the profit was left to maintain the business and the rest was shared according to their investments. Find how much each got. (5 marks)
-
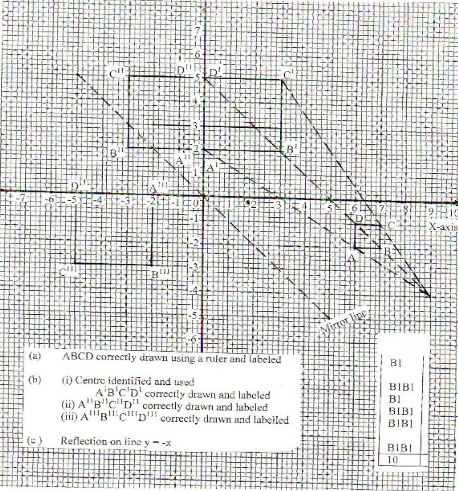
- On the grid provided draw the square whose vertices are A(6, -2), B(7, -2), C(7, -1) and D(6, -1) (1 mark)
- On the same grid draw
- A1B1C1D1 the image of ABCD, under an enlargement scale factor 3, Centre (9, -4) (3 marks)
- A11B11C11D11, the image A1B1C1D1 under a reflection in the line x = 0 (2 marks)
- A111B111C111D111, the image of A11B11C11D11 under a rotation of +900 about the origin. (2 marks)
- Describe a single transformation that maps A1B1C1D1 onto A111B111C111D111. (2 marks)
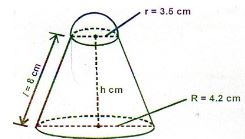
- The figure below shows a solid made up of a conical frustum and a hemispherical top. The dimensions are as indicated.
The top radius r = 3.5cm, bottom radius R = 4.2cm, slant height l = 8cm and the height of the frustum part is h cm.- Find the surface area of the solid (Take = 22/7) (5 marks)
- If a similar solid has a total surface area of 81.51cm2, determine the radius of its base, to the nearest whole number (1 mark)
-
- Find the height h of the frustum. (1 mark)
- Hence determine the volume of the solid (3 marks)
- Two towns A and B are 80km apart. Juma started cycling from town A to town B at 10.00am at an average speed of 40km/h. Mutuku started his journey from town B to town A at 10.30am and traveled by car at an average speed of 60km/h
Calculate:-
- The distance from town A when Juma and Mutuku met (5 marks)
- The time of the day when the two met (2 marks)
- Kamau started cycling from town A to town B at 10.20am. He met Mutuku at the same time as Juma did. Determine Kamau’s average speed. (3 marks)
-
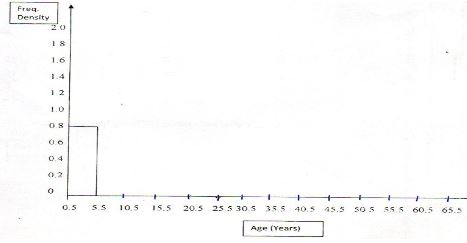
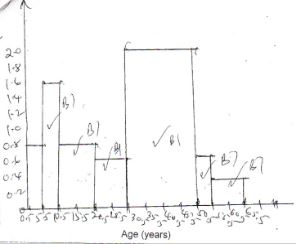
- The following data shows the sample of age distribution of the people who reside in a certain village in years, in Nandi County
Age group Frequency 1 - 5
6 - 10
11 - 20
21 - 30
31 - 50
51 - 55
56 - 654
8
8
6
40
3
3- Complete the histogram of the given data below (6 marks)
- Calculate the mean age of the given sample in the village (4 marks)
- Complete the histogram of the given data below (6 marks)
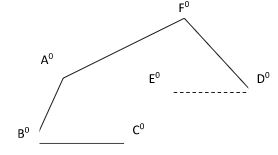
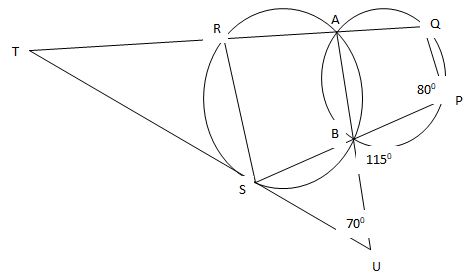
- The figure below shows two circles ABPQ and ABSR intersecting at A and B. PBS, QART and ABU are straight lines. The line UST is a tangent to the circle ABSR at S. Angle BPQ = 80°, angle PBU = 115° and angle BUS = 70°
Find the values of the following angles, stating your reasons in each case.- ˂BAR (2 marks)
- ˂STR (2 marks)
- ˂BSU (2 marks)
- ˂BRS (2 marks)
- ˂SBU (2 marks)
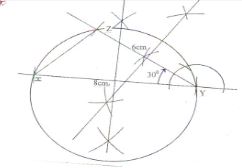
- Using a pair of compasses and ruler only,
- Construct triangle XYZ such that XY = 8cm, YZ = 6cm and angle XYZ = 300 (3 marks)
- Measure the length of XZ (1 mark)
- Draw a circle that touches the vertices X, Y and Z. (2 marks)
- Measure the radius of the circle (1 mark)
- Calculate the area of the circle outside the trangle to 2 d.p. (3 marks)
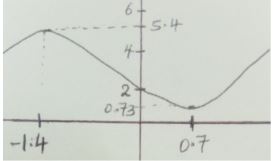
- The function y = x3 + x2 – 3x + 2 represents a curve.
- Find the gradient function of the curve (1 mark)
- Find the turning points of the curve and distinguish between them. (6 marks)
- Hence sketch the curve y = x3 + x2 – 3x + 2 (3 marks)
Marking Scheme
- 6(2 x 22/5) = 264/5
6 (2 x 5)= 5
112/5 ÷ 264/5 = 14/33
1/2 + 14/33 = 61/66
6 (8 x 3/22) = 72/11
1/2 x 72/11 = 36/11
61/66 ÷ 36/11 = 61/216 - (y² + x²) (y + x) (y – x)
y( y + x) (y – x)
y² + x²
y - 22x-1 x 2-3 + 3x = 26x +2
2x -1 – 3 + 3x = 6x + 2
x = - 6 - Customers selling price
=( 90/100 + 24,000)
= 21,600
100 x 21,600
120
= 18,000 - No. xy
x + y = 12
10y + x – 15 = 2(10x + y)
8(12 – x) -19x = 15
x = 3 y = 9
Original number 39 - 9.4522 = 89.34
1/63.37= 0.01578
89.35578 - L.S.F = ³√6750/2000 = 1.5
Radius of the large container = (15.5 x 1.5) x ½ = 11.625cm
= 11.6cm -
= 2i – 4j + k
/AB/ = √(22 + (-4)2 + 12)
=√ 21
= 4.583 -
15 = 12
Sin 30° sin θ
θ = 23.58°
n = 180 – 30 – 23.58 = 126.42°
Bearing = 180 + 126.42
= 306.42° - 3 – 2x ˂ x
3 ˂ 3x
1 ˂ x
3x ≤ 2x + 5
x ≤ 5 1 ˂ x ≤ 5
2,3,4,5 - 4 – x = 1/7
2x + 1
28 - 7x = 2x + 1, x = 3
y – 3 = -7
x + 1
y = -7x - 4 -
˂ LNK = 30°
˂ PNK = 70°
x = 360° – (30° +70°) = 260° -
- Volume = 63000/7
= 9000cm3
Volume L (15 x 12) - (12 x 10) h = 9000
60h = 9000
h = 1.5m -
- Jane: Mary
5 : 4
Dev: Div :Re
4 : 5 : 6
Dev = 4/15 x 81000 = sh. 21600
Div = 5/15 x 81000 = 27000
Mary got 4/9 x 27000 = 12000
- Jane: Mary
-
- D = ½ x 80 ( 24 + 16)
= 1600m - Decelaration = 20m/s2
- D = ½ x 80 ( 24 + 16)
-
- let the constant amount be x
Peter - (3/8 x ) / =
John’s - 2/5 (5/8x ) /=
= ¼ x /=
Remaining 3/8x - 18,000
x = 48,000
Therefore the original amount is 48,000 - John received
(1/4 x 48,000)
= 12,000/= - Business maintenance
(1/3 x 12,000)
= 4,000/=
Balance = 8,000
Ratios: Peter - (3/8 x 48,000)
= Ksh. 18,000/=
John - (1/4 x 48,000)
= 12,000/=
Caro - (1/3 x 18,000)
= 6,000/=
Ratio: 18,000 : 12,000 : 6,000
3 : 2 : 1
Peter got 3/6 x 8,000 + 18,000
= Ksh. 22,000/=
John got 2/6 x 8,000
= Ksh. 14,677/=
Caro got 1/6 x 8,000 + 18,000
= Ksh. 7,333/=
- let the constant amount be x
-
-
- bottom = 22/7 x 4.22 = 55.44cm2
Top = 4 x 22/7 x 3.52 x ½ = 77cm2
Curved = 22/7 x 8 x (4.2 + 3.5) = 193.6cm2
TSA = 77 + 55.44 + 193.6 = 326.04cm2 - r/1.2 = √81.51/326.04
r = 2.1cm -
- H = √(82 – 0.72)
= 7.97cm - volume = 1/3 x 22/7 x 7.97 (4.22 +3.5 +4.2 x 3.5) + 1/2 x 4/2 x 22/7 x 3.53
= 1/3 x 22/7 x 7.97 x 44.59 + 89.83
= 462.13 cm3
- H = √(82 – 0.72)
- bottom = 22/7 x 4.22 = 55.44cm2
-
-
- Relative speed = (40 + 60) km/h = 100km/h
Relative Distance = 80km – 0.5h x 40km/h = 60km
Time = distance/ relative speed = 60/100 = 0.6 hrs
Distance from A = 20km + 0.6 x 40 = 44km - 10.30am + 36 minutes = 11.06am
- Relative speed = (40 + 60) km/h = 100km/h
- Time taken by Kamau = 11.06am – 10.20am = 46 minutes
Average Speed = 44/ (46/60) = 57.39km/h
-
-
-
-
Class x F fx 1 - 5
6 - 10
11 - 20
21 - 30
31 - 50
51 - 55
56 - 653
8
15.5
25.5
40.5
53
60.54
8
8
6
40
3
312
64
124
153
1620
159
181.572 2313.5
Mean= Σfx/Σf
= 2313.5
72
= 32.13
-
-
- BAR ˂ QAB = 100° – opposite angles in a quadrilateral add up to 1800
˂ BAR = 80° – angles in a straight line add up to 1800 - STR ˂ STR = 180 – (80 + 70°)
= 30 – angles in a straight line add up to 180° - BSU ˂ UBS = 180 – 115° = 65° – angles in a straight line add up to 180°
˂ BSU = 45° – angles in a straight line add up to 180° - BRS ˂ SBA = 115° – vertically opposite angles are equal
˂ BRS = 65 – opposite angles in a cyclic quadrilateral add up to 1800 - SBU - 180 – 115 = 65° – angles on a straight line
- BAR ˂ QAB = 100° – opposite angles in a quadrilateral add up to 1800
-
- Xy and YZ
<XYZ construction of <30°
completing ΔXYZ - XZ = 4.0cm ± 0.1
- Bisecting any 2 sides curve circle
- Radius = 4.2cm ± 0.1
- Area of circle → 3.142 (4.2)2
Area = 55.425 - 12
= 43.43cm2
- Xy and YZ
-
- dy/dx = 3x2 + 2x -3
- 3x2 + 2x – 3 = 0
x = -2 ± √(4 + 36)
6
x = -2 ± 6.325
6
x = - 1.3875 or 0.7208
d²y = 6x + 2
dx²
6(-1.3875) + 2 = -6.325
6(0.7208) + 2 = 6.3248
(-1.3875, 5.416) is maximum turning point
(0.7208, 0.7316) is minimum turning point - y – intercept = 2
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - KCSE 2022 Mock Exams Set 2.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students