INSTRUCTIONS.
- Answer all the questions in the spaces provided.
QUESTIONS
SECTION 1 (50mks)
- The sum of n terms of the sequence:
3,9,15,21…. Is 7500- Find the 20th term of the sequence. (2mks)
- Determine the value of n. (2mks)
- A quadratic curve passes through the points (-2, 0) and (1, 0). Find the equation of the curve in the form y = ax2+bx+c, where a, b and c are constants. (2mks)
- Make h the subject of the formula. (2mks)
q= 1+rh
1-ht - P (1,2) and Q(9,8) are the points on the ends of the diameter of a circle. Write down in terms of x and y the equation of the circle in the form: ax2+by2+x+y+c=0. (3mks)
- In the figure below, O is the centre of the circle and AT is a tangent to the circle at A. AT = 2√6cm and DT=4cm.
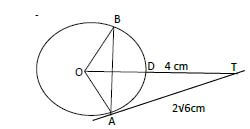
Determine:- OA (2mks)
- The value of angle AOB (2mks)
- In a transformation, an object with an area of 5cm2 is mapped onto an image whose area is 30cm2. Given that the matrix of the transformation is x
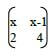
- Find the value of x. (2mks)
- Hence determine the inverse of the matrix
- The co-ordinates of P are (0,7) and Q are (3.5, 1.4). A point S divides PQ externally in the ratio 9:2. Find the co-ordinates of S. (3mks)
- The top of a coffee table is a regular hexagon. Each side of the hexagon measures 50.0cm, find the percentage error in calculating the perimeter of the top of the table. (3mks)
- The figure below represents a cuboid ABCDEFGH. AB=60cm, BC=11cm and CH=10cm.
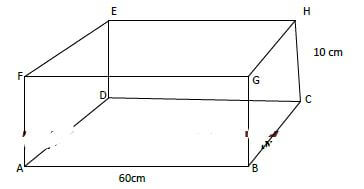
Calculate the angle between EB and plane EFGH. (3mks) -
- Expand and simplify the expression
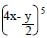 up to the third term. (2mks)
up to the third term. (2mks) - Hence use the expansion in (a) above to approximate the value of (39.6)5 correct to 3 significant figures. (2mks)
- Expand and simplify the expression
- A solution was gently heated, its temperature readings taken at intervals of 1 minute and recorded as shown in the table below:
Time(min) 0 1 2 3 4 5 Temperature (ºC) 4 5.2 8.4 14.3 16.8 17.5 - On the grid provided below, draw the time – temperature graph. (2mks)
- Use the graph to find the average rate of change in temperature between t=1.8 and t=3.4. (2mks)
- The shortest distance between two points A(40ºN,20ºW) and B(ѲºS,20ºW) on the surface of the earth is 8008km. given that the radius of the earth is 6370km, determine the position of B. (Take π=22/7). (3mks)
- Simplify √3 (2mks)
√3 - √2 - The table below shows income tax rates in a certain year.
In that year, a monthly personal tax relief of ksh. 1056 was allowed. Calculate the monthly income tax paid by an employee who earned a monthly salary of kshs. 32,500. (4mks)Monthly income in Kshs. Tax rate in each shilling Up to 9680 10% From 9681 to 18800 15% From 18801 to 27920 20% From 27921 to 37040 25% Over 37040 30% - Three types of beverages are mixed in the ration 1:3:5 respectively. Type A costs sh 26, type B costs sh 28 and type C sh 32, per packet. Find the cost of the mixture per packet. (3mks)
- The gradient of a curve is given by dy/dx = x2- 4x+3. The curve passes through the point (1,0). Find the equation of the curve. (3mks)
SECTION II (50MKS)
- The hire purchase (H.P) price of an electronic device was ksh. 276,000. A deposit of ksh 60,000 was paid followed by 18 equal monthly installments.
- Calculate the monthly installment. (2mks)
- The cash price of the electronic device was 10% less than the hire purchase (H.P) price. Calculate the cash price. (2mks)
- Madam Kanini decided to buy the electronic device in cash. She was allowed a 5% discount on the cash price, she took a bank loan to buy the device. The bank charged compound interest on the loan at the rate of 20% p.a. the loan was repaid in 2 years.
- Calculate the amount repaid to the bank by the end of the second year. (3mks)
- Express as a percentage of the hire purchase (HP) price, the difference between the amount repaid to the bank and the hire purchase price. (3mks)
- An examination involves a written test and a practical test. The probability that a candidate passes the written test is 6/11. If the candidate passes the written test, then the probability of passing the practical test is 3/5, otherwise it would be 2/7.
- Illustrate this information on a tree diagram. (2mks)
- Determine the probability that a candidate is awarded:
- For passing both tests. (2mks)
- For passing the written test. (2mks)
- Determine the probability that the candidate;
- Passes one test. (2mks)
- Fails for not passing the written test. (2mks)
- Construct triangle PQR with PQ= 7.2cm, QR=6cm and <PQR=48º. (3mks)
- The locus L1, of points equidistant from P and Q and Locus L2 of points equidistant from P and R, meet at M. Locate M hence measure QM. (4mks)
- A point X moves within triangle PQR such that QX ≥QM. Shade and label the locus of X. (3mks)
- Triangle PQR shown on the grid below has vertices P(5,5), Q(10,10) and R(10,15)
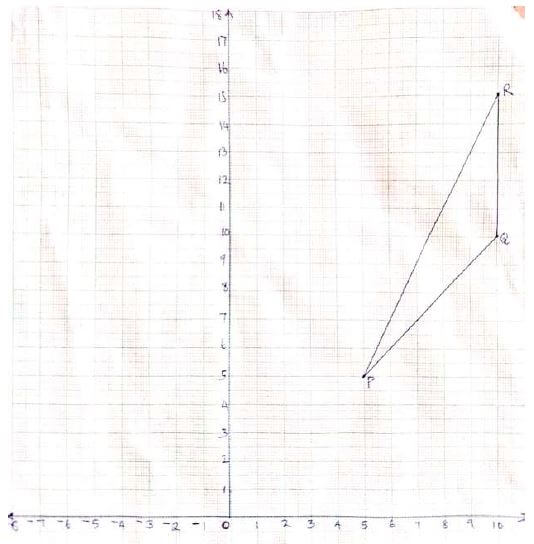
- Find the coordinates of the points P΄Q΄ and R΄ the images of P,Q and R respectively under transformation M whose matrix is [- 0.6 0.8] (3mks)
[ 0.8 0.6]
Given that M is a reflection:- Draw triangle P΄Q΄R΄ and the mirror line of the reflection. (2mks)
- Determine the equation of the mirror line of the reflection. (2mks)
- Triangle P˝Q˝R˝ is the image of triangle P΄Q΄R΄ under reflection N, where N is a reflection in the Y-axis.
- Determine triangle P˝Q˝R˝ (1mk)
- Determine a 2x2 matrix equivalent to the transformation NM. (2mks)
- Find the coordinates of the points P΄Q΄ and R΄ the images of P,Q and R respectively under transformation M whose matrix is [- 0.6 0.8] (3mks)
- In the figure below, PR is the diameter of the circle with centre O. Points P, Q, R and S are on the circumference of the circle. Angle PRQ = 72⁰ , QS = QP and line USV is a tangent to the circle at S.
Giving reasons, calculate the size of: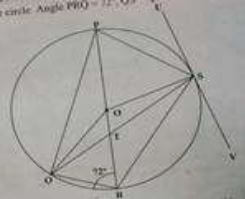
- ∠QPR (2 marks)
- ∠PQS (2 marks)
- ∠OQS (2 marks)
- ∠RTS (2 marks)
- ∠RSV (2 marks)
- Three quantities R,S and T are such that R varies directly as S and inversely as the square of T.
- Given that R= 480 when S=150 and T=5, write an equation connecting R, S and T. (4mks)
-
- Find the value of R when S=360 and T=1.5. (2mks)
- Find the percentage change in R if s increase by 5% and T decreases by 20%. (4mks)
- For a C B C inservice training course for teachers, at least four (4) but not more that nine(9) teachers are to be chosen per school. The ratio of the number of male teachers to the number of female teachers must be less than 2:1 and there must be more males than females. If x and y represent the number of male teachers and female teachers respectively:
- Write down in their simplest form the inequalities that x and y must satisfy. (4mks)
- On the gird provided below, represent the inequalities on the graph. (4mks)
- Use the graph to determine the composition of the training group of:
- The largest size. (1mk)
- The smallest size. (1mk)
- The equation of a curve is given by y=5x- ½ x2.
- On the grid provided below, draw the curve of y=5x- ½ x2 for 0≤x≤6. (3mks)
- By integration, find the area bounded by the curve, the line x=6 and the x-axis. (3mks)
- On the same grid, draw the line y=2x. (1mk)
- Determine the area bounded by the curve and the line y=2x. (3mks)
MARKING SCHEME
SECTION 1 (50mks)
- The sum of n terms of the sequence:
3,9,15,21…. Is 7500- Find the 20th term of the sequence. (2mks)
a = 3
d = 6
nth = a + (n - 1)d
∴20th = 3 + (20 - 1)6
=117 - Determine the value of n. (2mks)
sn = n/2 {2a + (n - 1)d}
7500 = n/2 {2 x 3 + (n - 1) 6}
15000 = 6n2
∴n2 = 2500
n = ± 50
= 50 terms
- Find the 20th term of the sequence. (2mks)
- A quadratic curve passes through the points (-2, 0) and (1, 0). Find the equation of the curve in the form y = ax2+bx+c, where a, b and c are constants. (2mks)
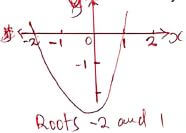
∴(x + 2) = 0
and (x - 1) = 0
let y = (x + 2) (x - 1)
=> y = x2 + x - 2 - Make h the subject of the formula. (2mks)
q= 1+rh
1-ht
q - qht = 1 + rh
q - 1 = rh + qht
q - 1 = h(r + qt)
∴ h = q - 1
r + qt - P (1,2) and Q(9,8) are the points on the ends of the diameter of a circle. Write down in terms of x and y the equation of the circle in the form: ax2+by2+x+y+c=0. (3mks)
ans = x2 + y2 - 10x - 10y + 25 = 0 - In the figure below, O is the centre of the circle and AT is a tangent to the circle at A. AT = 2√6cm and DT=4cm.

Determine:- OA (2mks)
let OD = x
TO x TD = TA2
(4 + x) 4 = (2√6)2
16 + 4x = 24
4x = 8
∴ x = 2 - The value of angle AOB (2mks)
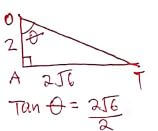
∴ θ = 67.8
∴ ∠ AOB = 2 x 67.8
= 135.6
- OA (2mks)
- In a transformation, an object with an area of 5cm2 is mapped onto an image whose area is 30cm2. Given that the matrix of the transformation is x
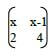
- Find the value of x. (2mks)
determinant = 4x - 2(x - 1)
= 2x + 2
area scale factor = 30/5
det = ASF
∴ 2x + 2 = 30/5
∴ x = 2 - Hence determine the inverse of the matrix
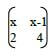
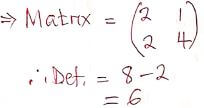
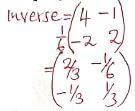
- Find the value of x. (2mks)
- The co-ordinates of P are (0,7) and Q are (3.5, 1.4). A point S divides PQ externally in the ratio 9:2. Find the co-ordinates of S. (3mks)
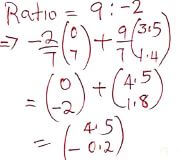
∴ s = (4.5, -0.2) - The top of a coffee table is a regular hexagon. Each side of the hexagon measures 50.0cm, find the percentage error in calculating the perimeter of the top of the table. (3mks)
n = 6 sides
actual perimeter = 50.0 x 6
= 300 cm
maximum per = 50.05 x 6
= 300.3
∴ Abs. error = 300.3 - 300
= 0.3
% error = 0.3 / 300 x 100
= 0.1 % - The figure below represents a cuboid ABCDEFGH. AB=60cm, BC=11cm and CH=10cm.

Calculate the angle between EB and plane EFGH. (3mks)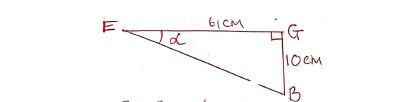
EG2 = 112 + 602
= 121 + 3600
EG = √3721
= 61 cm
Tan ∝ = 10/61
= 0.1639
∴ ∝ = 9.3º -
- Expand and simplify the expression
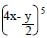 up to the third term. (2mks)
up to the third term. (2mks)
(4x)5 + (4x)4(-y/2) + (4x)3(-y/2)2 + ..............
1024x5 + 5 x 256(-y/2) + 10x64x3(-y2/4) + ............
1024x5 - 6404x4y + 160x3y2 + ............ - Hence use the expansion in (a) above to approximate the value of (39.6)5 correct to 3 significant figures. (2mks)
Let 39.6 = 40 - 0.4
=> 39.65 = (40 - 0.4)5
comparing:
4x = 40
; x = 10
-y/2 = 0.4
∴ y = 0.8
substituting;
1024(105) - 640(104) x 0.8 + 160(103)(0.8)2 + ......
= 102400000 - 5120000 + 102400
= 97382400
- Expand and simplify the expression
- A solution was gently heated, its temperature readings taken at intervals of 1 minute and recorded as shown in the table below:
Time(min) 0 1 2 3 4 5 Temperature (ºC) 4 5.2 8.4 14.3 16.8 17.5 - On the grid provided below, draw the time – temperature graph. (2mks)
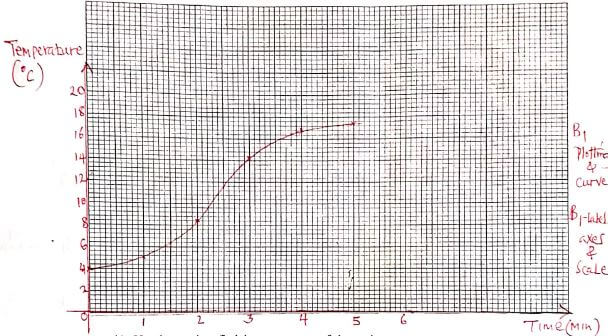
- Use the graph to find the average rate of change in temperature between t=1.8 and t=3.4. (2mks)
15.6 - 7.6 = 8
3.4 - 1.8 1.6
= 5ºc/min
- On the grid provided below, draw the time – temperature graph. (2mks)
- The shortest distance between two points A(40ºN,20ºW) and B(ѲºS,20ºW) on the surface of the earth is 8008km. given that the radius of the earth is 6370km, determine the position of B. (Take π=22/7). (3mks)
let ∝ = 40 + Ѳ
(40 + Ѳ) x 2π x 6370 = 8008
360
∴ Ѳ = 32.01º
∴ position B (32.01ºS, 20ºN) - Simplify √3 (2mks)
√3 - √2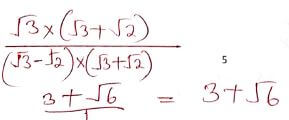
- The table below shows income tax rates in a certain year.
In that year, a monthly personal tax relief of ksh. 1056 was allowed. Calculate the monthly income tax paid by an employee who earned a monthly salary of kshs. 32,500. (4mks)Monthly income in Kshs. Tax rate in each shilling Up to 9680 10% From 9681 to 18800 15% From 18801 to 27920 20% From 27921 to 37040 25% Over 37040 30%
first 9680 x 10/100 = 968
second 9120 x 15/100 = 1368
third 9120 x 20/100 = 1824
last 4580 x 25/100 = 1145
gross tax = 5305
income tax = 5305 - 1056
= sh. 4249 - Three types of beverages are mixed in the ration 1:3:5 respectively. Type A costs sh 26, type B costs sh 28 and type C sh 32, per packet. Find the cost of the mixture per packet. (3mks)
1 + 3 + 5 = 9
type A -> 26 x 1 = sh.26
Type B -> 28 x 3 = Sh.160
Total cost = sh 270
∴ cost per packet = sh 270/9 = sh 30 - The gradient of a curve is given by dy/dx = x2- 4x+3. The curve passes through the point (1,0). Find the equation of the curve. (3mks)
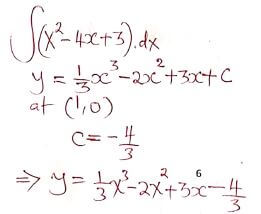
SECTION II (50MKS)
- The hire purchase (H.P) price of an electronic device was ksh. 276,000. A deposit of ksh 60,000 was paid followed by 18 equal monthly installments.
- Calculate the monthly installment. (2mks)
276000 - 60000
= 216 000
216000
18
= sh 12 000 - The cash price of the electronic device was 10% less than the hire purchase (H.P) price. Calculate the cash price. (2mks)
90 x 276 000
100
= sh 248 000 - Madam Kanini decided to buy the electronic device in cash. She was allowed a 5% discount on the cash price, she took a bank loan to buy the device. The bank charged compound interest on the loan at the rate of 20% p.a. the loan was repaid in 2 years.
- Calculate the amount repaid to the bank by the end of the second year. (3mks)
95/100 x 248 000
= sh 235 980
Let principal = sh 235 980
Rate = 20%
n = 2 yrs
A = P(1 + r/100)n
= 235 980 (1 + 20/100)R
= sh 339, 811. 20 - Express as a percentage of the hire purchase (HP) price, the difference between the amount repaid to the bank and the hire purchase price. (3mks)
339,811.20 - 276,000
=sh 63, 811.20
63811.20 x 100
276000
= 23.12%
- Calculate the amount repaid to the bank by the end of the second year. (3mks)
- Calculate the monthly installment. (2mks)
- An examination involves a written test and a practical test. The probability that a candidate passes the written test is 6/11. If the candidate passes the written test, then the probability of passing the practical test is 3/5, otherwise it would be 2/7.
- Illustrate this information on a tree diagram. (2mks)
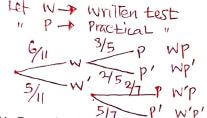
- Determine the probability that a candidate is awarded:
- For passing both tests. (2mks)
p(wp)
= 6/11 x 3/5
= 18/55 - For passing the written test. (2mks)
p(wp) or p(wp')
6/11 x 3/5 + 6/11 x 2/5
= 6/11
- For passing both tests. (2mks)
- Determine the probability that the candidate;
- Passes one test. (2mks)
p(wp') or p(w'p)
6/11 x 2/5 + 5/11 x 2/7
= 1474/4235 - Fails for not passing the written test. (2mks)
p(w'p')
5/11 x 5/7
= 25/77
- Passes one test. (2mks)
- Illustrate this information on a tree diagram. (2mks)
- Construct triangle PQR with PQ= 7.2cm, QR=6cm and <PQR=48º. (3mks)
- The locus L1, of points equidistant from P and Q and Locus L2 of points equidistant from P and R, meet at M. Locate M hence measure QM. (4mks)
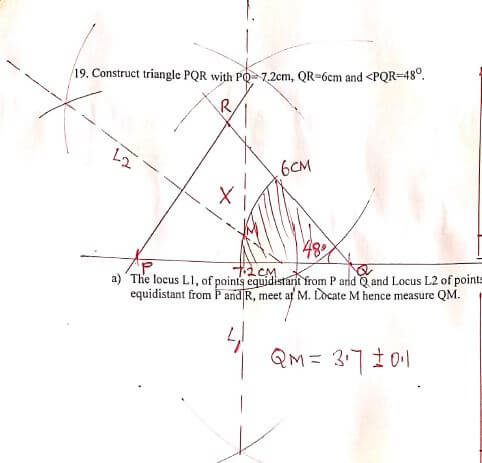
- A point X moves within triangle PQR such that QX ≥QM. Shade and label the locus of X. (3mks)
- The locus L1, of points equidistant from P and Q and Locus L2 of points equidistant from P and R, meet at M. Locate M hence measure QM. (4mks)
- Triangle PQR shown on the grid below has vertices P(5,5), Q(10,10) and R(10,15)
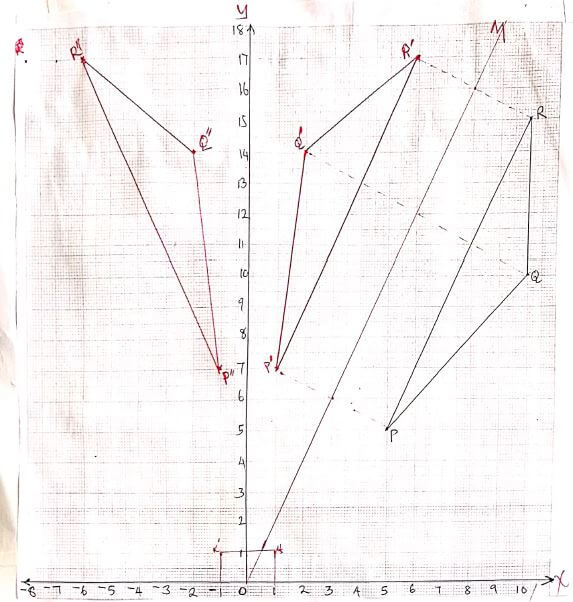
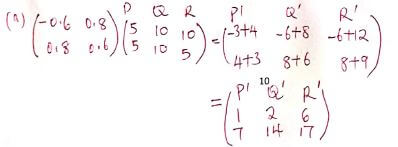
- Find the coordinates of the points P΄Q΄ and R΄ the images of P,Q and R respectively under transformation M whose matrix is [- 0.6 0.8] (3mks)
[ 0.8 0.6]
Given that M is a reflection:- Draw triangle P΄Q΄R΄ and the mirror line of the reflection. (2mks)
line y = 2x drwan/identified - Determine the equation of the mirror line of the reflection. (2mks)
gradient of m = 2 units
let y = mx + c
y = 2x + 0
∴ y = 2x
- Draw triangle P΄Q΄R΄ and the mirror line of the reflection. (2mks)
- Triangle P˝Q˝R˝ is the image of triangle P΄Q΄R΄ under reflection N, where N is a reflection in the Y-axis.
- Determine triangle P˝Q˝R˝ (1mk)
in the graph - Determine a 2x2 matrix equivalent to the transformation NM. (2mks)
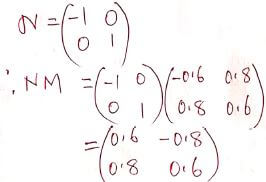
- Determine triangle P˝Q˝R˝ (1mk)
- Find the coordinates of the points P΄Q΄ and R΄ the images of P,Q and R respectively under transformation M whose matrix is [- 0.6 0.8] (3mks)
- In the figure below, PR is the diameter of the circle with centre O. Points P, Q, R and S are on the circumference of the circle. Angle PRQ = 72⁰ , QS = QP and line USV is a tangent to the circle at S.
Giving reasons, calculate the size of:
- ∠QPR (2 marks)
- ∠PQS (2 marks)
- ∠OQS (2 marks)
- ∠RTS (2 marks)
- ∠RSV (2 marks)
- Three quantities R,S and T are such that R varies directly as S and inversely as the square of T.
- Given that R= 480 when S=150 and T=5, write an equation connecting R, S and T. (4mks)
ans = R = 80S
T2 -
- Find the value of R when S=360 and T=1.5. (2mks)
R = 80 x 360
152
= 12, 800 - Find the percentage change in R if s increase by 5% and T decreases by 20%. (4mks)
Ans = 64.06% increase
- Find the value of R when S=360 and T=1.5. (2mks)
- Given that R= 480 when S=150 and T=5, write an equation connecting R, S and T. (4mks)
- For a C B C inservice training course for teachers, at least four (4) but not more that nine(9) teachers are to be chosen per school. The ratio of the number of male teachers to the number of female teachers must be less than 2:1 and there must be more males than females. If x and y represent the number of male teachers and female teachers respectively:
- Write down in their simplest form the inequalities that x and y must satisfy. (4mks)
- x + y ≥ 4 (at least 4 teachers)
- x + y ≤ 9 (not more than 9 teachers)
- x:y < 2:1
x < 2y - x>y (more males than females)
- On the gird provided below, represent the inequalities on the graph. (4mks)
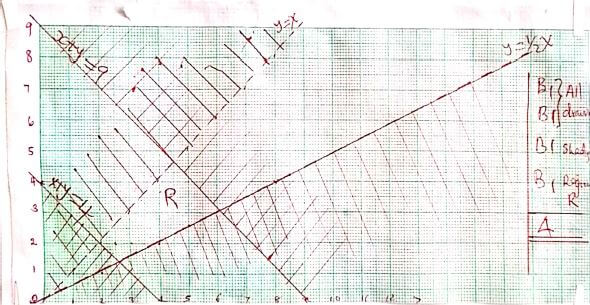
- Use the graph to determine the composition of the training group of:
- The largest size. (1mk)
integral values (5,4)
5 + 4 = 9 teachers - The smallest size. (1mk)
integral values (3,2)
3 + 2 = 5 teachers
- The largest size. (1mk)
- Write down in their simplest form the inequalities that x and y must satisfy. (4mks)
- The equation of a curve is given by y=5x- ½ x2.
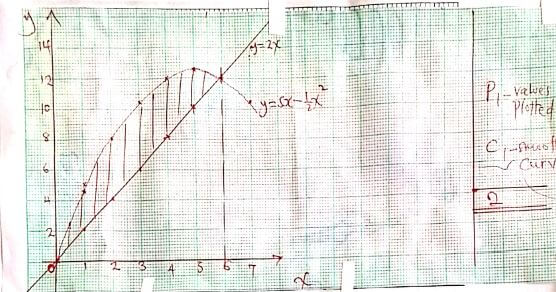
- On the grid provided below, draw the curve of y=5x- ½ x2 for 0≤x≤6. (3mks)
x 0 1 2 3 4 5 6 y 0 4.5 8 10.5 12 12.5 12 - By integration, find the area bounded by the curve, the line x=6 and the x-axis. (3mks)
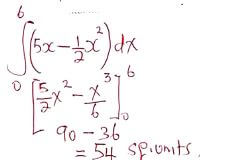
- On the same grid, draw the line y=2x. (1mk)
Line drawn (must be straight) - Determine the area bounded by the curve and the line y=2x. (3mks)
A = 54 - Area of triangle
= 54 - 1/2 x 6 x 12
= 54 - 36
= 18 sq.units
- On the grid provided below, draw the curve of y=5x- ½ x2 for 0≤x≤6. (3mks)
Download Mathematics Paper 2 Questions and Answers - Lanjet Joint Mock Exams 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students
