Mathematics Paper 1 Questions and Answers - ACK Diocese Mumias Joint Evaluation Mock 2022

Questions

SECTION I (50 Marks)
Answer all the questions in this section in the spaces provided.

1. Without using mathematical tables or calculator evaluate: 7³/₅ - 1/3(1¹/₄ + 3 ¹/₃) x 2²/₅ (3 marks)
2. Lessons in Nyamasaria and Kasagam Secondary schools take 30 minutes and 40 minutes respectively.
   The two bells ring simultaneously at 7.50 a.m. How many times will they ring together again between 7.50 a.m. and 3.00 p.m. (3 marks)
3. Use table of squares and square roots to find the value of x = √(0.0472² +0.1236²) (3 marks)
4. A straight line L₁ whose equation is 3y− 2x=−2 meets the x – axis at R. Determine the coordinates of R. (2 marks)
5. Given that tanα=0.75, without using mathematical tables or calculator find cos(90−α). (2 marks)
6. A Kenyan company received M Us dollars. The money was converted into Kenya Shillings in a bank which buys and sells foreign currencies as shown below.
   

   	Buying (Kshs)	Selling  (Kshs)
   1 Sterling Pound	125.78	126.64
   1 US Dollar	75.66	75.86

   
   
   1. If the company received Kshs.15, 132, 000, calculate the amount, M Us Dollars. (2 marks)
   2. The company exchanged the above Kenyan shillings into Sterling pounds to buy a car in Britain. Calculate the cost of the car to the nearest Sterling Pound. (2 marks)
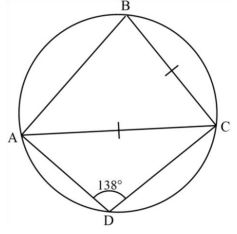
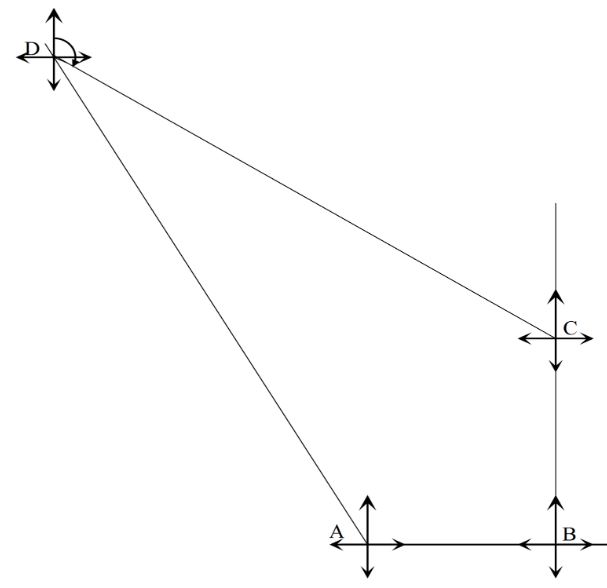
7. In the figure below, A, B, C and D are points on the circumference. Chord BC = AC and angle ADC = 138°
   
   Giving reasons, calculate the size of angle ACB. (3 marks)
8.  
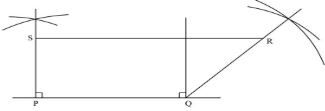
   1. Using a ruler and a pair of compasses only, construct a quadrilateral PQRS in which PQ = 5 cm, PS = 3 cm, QR = 4 cm, <PQR=135° and Angle SPQ is a right angle. (2 marks)
   2. The quadrilateral PQRS represents a plot of land drawn to a scale 1:4000. Determine the actual length of RS in meters. (2 marks)
9. Find the ratio a:c if a:b = 2:5 and b:c = 2:3. (2 marks)
10. Simplify the expression:(3 marks)
    2p² -3p - 5
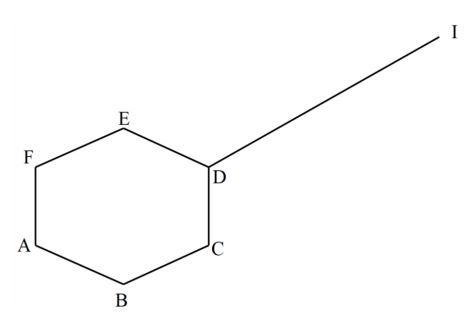
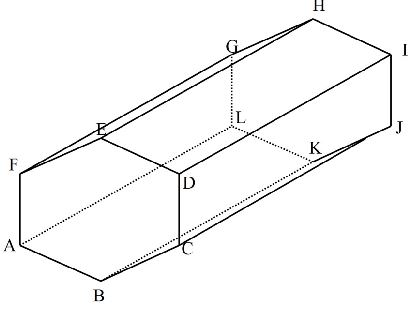
       4p² - 25
11. In the figure below ABCDEF is a uniform cross – section of a solid. Given that DI is one of the visible edges of the solid, complete the sketch showing the hidden edges withbroken lines. (3 marks)
    
    
    1. Given the inequalities 2x−3≤4x+7<x+13, solve the inequalities and represent the solution on a number line. (3 marks)
12. The position vector of points A and B are −10i− 6j+ 9k and −5i+k respectively.
    Calculate |AB| leaving your answer in surd form. (3 marks)
13. Two numbers p and q are such that p³ × q=135 , find p and q. (3 marks)
14. A circle centre O has the equation x² +y² = 4. The area of the circle in the first quadrant is divided into five vertical strips each of width 0.4 cm.
    1. Use the equation of the circle to complete the table below for values of y correct to two decimal places. (1 mark)
       

       x	0	0.4	0.8	1.2	1.6	2.0
       y	2.00			1.60		0.00

    2. Use trapezium rule to estimate the area of the circle. (3 marks)
    3. Four interior angles of an irregular polygon are each 155°, while the rest are each 160°. Find the number of sides of the polygon. (3 marks)

SECTION II (50 Marks)
Answer only five questions in this section in the spaces provided.

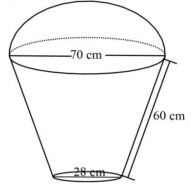
17. The figure below represent a model of a solid structure in the shape of a frustum of a cone with hemispherical top. The diameter of hemispherical part is 70 cm and is equal to the diameter of the frustum. The frustum has a base diameter of 28 cm and a slant height of 60 cm.
    
    Calculate:
    1. The area of the hemispherical surface. (2 marks)
    2. The slant height of the cone from which the frustum was cut. (3 marks)
    3. The total surface area of the model. (5 marks)
18. A matatu and Nissan left town A for town B 240 km away at 8:00 a.m. travelling at 90 km/hr and 120 km/hr respectively. After 20 minutes the Nissan had a puncture which took 30 minutes to mend.
    1. At what time did the Nissan catch up with the matatu? (5 marks)
    2. How far from town A did the Nissan catch up with the matatu? (2 marks)
    3. At what time did the matatu reach town B? (3 marks)
19. A number of people are asked to cut 20 cm length of string without measuring. Later 100 cm pieces are collected and measured correct the nearest 0.1 cm. The data below was obtained.
    

    Length	18.0 −18.4	18.5−18.9	19.0 −19.4	19.5 −19.9	20.0− 20.4	20.5− 20.9	21.0 − 21.4	21.5− 21.9
    Frequency	5	8	30	x	10	20	10	4

    1. Find :
       1. The value of x. (1 mark)
       2. The modal class. (1 mark)
    2. Calculate:
       1. The mean. (4 marks)
       2. The median. (4 marks)
20. Four cities A, B, C and D are such that town B is 1500 km due East of town A. Town C is 1800 km due North of town B. Town D is on a bearing of 330° from town A and on a bearing of 300° from C.
    1. Use a ruler and compasses only to show the position of town A, B, C and D. (Take a scale of 1 cm = 300 km ). (5 marks)
    2. Determine:
       1. The distance AD. (2 marks)
       2. The distance CD. (2 marks)
       3. The bearing of town D from town B. (1 mark)
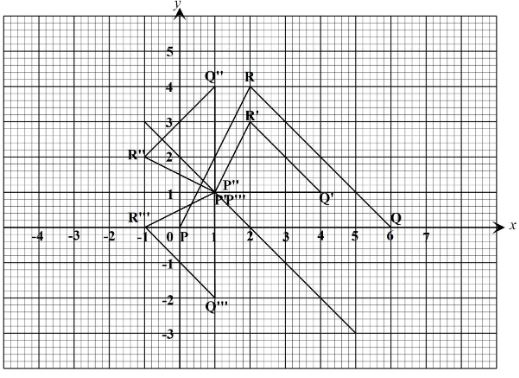
21. The vertices of triangle PQR are P(0,0), Q(6,0) and R(2,4) .
    1. Draw triangle PQR on the grid provided. (1 mark)
    2. Triangle P'Q'R'is the image of a triangle PQR under an enlargement scale factor and centre (2,2). Write down the coordinates of triangle P'Q'R'and plot on the same grid. . (3marks)
    3. Draw triangle P''Q''R''the image of triangle P'Q'R'under a positive quarter turn about point (1,1). (2 marks)
    4. Draw a triangle P'''Q'''R''' the image of triangle P''Q''R'' under reflection in the line y= 1. (2 marks)
    5. Describe fully a single transformation that maps triangle P'''Q'''R''' onto triangle P'Q'R'. (2 marks)
22.         
    1. Find the inverse A−1 of the matrix: A= (2 marks)
    2. Rose bought 20 bags of oranges and 15 bags of mangoes for a total of Kshs.9 500. Chumo bought 15 bags of oranges and 10 bags of mangoes for a total of Kshs.6 750. If the price of a bag of oranges is x and that of mangoes is y:
       1. Form two equations to represent the information above. (2 marks)
       2. Hence use the matrix A−1 above to find the price of one bag of each item.(3 marks)
    3. The price of each bag of oranges was increased by 10% and that of mangoes reduced by 10%. The businesswomen (Rose and Chumo) bought as many oranges and as many mangoes as they bought earlier. Find by matrix method the total cost of oranges and mangoes that the businesswomen bought after the percentage change. (3 marks)
23.         
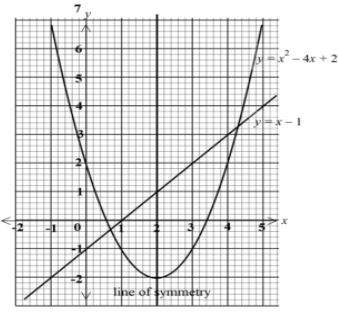
    1. Fill the table below for the function y=x² −4x+ 2 for −1≤ x≤5. (2 marks)
       

       x	-1	0	1	2	3	4	5
       y

    2.   
       1. Draw the graph of the function y=x² −4x+ 2 for −1≤ x≤5. (3 marks)
       2. On the same axes, draw line y=x−1. (1 mark)
    3. Determine the values of x at the points of intersection between the curve y=x2 −4x+ 2 and line y=x−1 (2 marks)
    4. Draw the line of symmetry of the curve hence state its equation. (2 marks)
24. The displacement s of a particle after t seconds is given by s =4t³ − ⁵/₂t² −3t +3.
    Determine the:
    1. Velocity of the particle when t =3 seconds. (3 marks)
    2. Value of t when the particle is instantaneously at rest. (3 marks)
    3. Displacement when the particle is instantaneously at rest. (2 marks)
    4. Acceleration of the particle when t =2 seconds. (2 marks)

Marking Scheme

1. ³⁸/₅  - ¹/₃ X ⁵⁵/₁₂ X ¹²/₅
   ³⁸/₅  - ¹¹/₃ =   14  -   55      
                               15
   =3¹⁴/₁₅
2. L.C.M (30,40)=120minutes (2 hours)
   Number of times = 1500hrs  -  0750hrs
                                       2hrs
   = 3 ⁷/₁₂ = 3 times
3. (0.0472)² =(4.72 x 10⁻²)²
   = 22.278 x 10⁻⁴ = 0.0022278
   (0.1236)² = (1.236 x 10⁻¹)²
   =1.528 x 10⁻² = 0.01528
   =√(0.0022278 + 0.01528)
   =√(1.751 X 10^-2)
   =0.13233
4. 3(0)−2x=−2
   x=1
   ⸫R(1,0)
5. Hypotenuse = √(4²+3²) = 5
   ⸫ Cos (90-α) =3/5
6.      
   1. M=   15132000  
                 75.66
      = 200 000 US Dollars
   2. 15132000
         126.64  
      =119488
7. <ABC = 42° Opposite angles in a cyclic quadrilateral add up to 180
   <BAC = 42° Base angles of an isosceles triangle are equal
   <ACB = 96° Sum of interior angles of a triangle add up to 180
8.    
   
   7.8cm x 40m
         1
   =312 ± 4m
9. a : b : c
   2 : 5
        2 : 3 ,
   4: 10: 15
   a:c= 4:15
10.    2p² + 2p - 5p - 5
     (2p + 5)(2p -5)
      (p + 1) (2p -5)  
     (2p -5)(2p + 5)
    
       P+1      .
       2p+ 5
11.    
    
12. 2x−3≤ 4x+7 
    −2x≤10
    x≥−5
    
    4x+7 <x+3 
    3x< 6
    x<2
    -5≤ x<2
    
13.      
    
    
14. p³×q =135
    p³×q = 3³×5
    p = 3
    q = 5
15.        
    1.    
       

       x	0	0.4	0.8	1.2	1.6	2.0
       y	2.00	1.96	1.83	1.60	1.20	0.00

             
    2. Area = ½ × 0.04 [(2.00+0.00)+2(1.96 +1.83+ 1.60+1.20)]
       = 0.2(2.00+13.18)
       =3.036cm²
16. (4x155)+160(n−4)=180(n−2)
    620+160n−640 =180n−360
    20n = 340 n =17sides
17.      
    1. S.A= 2XX352
       =7700cm2 x _____
         x+60   =     x    
           35            14
       14(x+60)= 35x
       14x−35x =−840
       −21x =−840
       x = 40
       ⸫ Slant height = 40 + 60 = 100cm
    2. Total Surface Area of the model:
       = 2πr² +(πRL−πrl)+πr²
       Curved S.A = ²²/₇(35x100−14x40r) = 92400cm²
       Base area: ²²/₇ x 14²
       = 616cm2
       Total Surface area of the model:
       = 7700 + 9240 + 616 =17 556cm²
18.    
    1. Matatu distance =    90 x 20    = 30km
                                          60
       Nissan distance =    120x30    = 40km
                                          60
       After 30 mins =     90x30       
                                      60
       =45 km
       Relative distance = (120 −90)= 30 km/hr Relative speed = 75−40 = 35 km
       Time taken to overtake = = 1 hour 10 mins time = 8 : 50 + 1: 10 = 10:00 a.m.
    2. Overtaking time = 10:00 - 8:00 = 2 hours
       Distance = 90 x 2
       = 180 km
    3. Time =      distance    =     240   
                        speed               90
       = 2 hours 40 minutes Arrival time = 8:00 + 2:40
       = 10 : 40 a.m.
19.    
    1. x =100−87 x =13
    2. Modal class : 19.0 – 19.4
       

       Length (cm)	x	f	fx	cf
       18.0−18.4 18.5−18.9 19.0−19.4 19.5−19.9 20.0−20.4 20.5−20.9 21.0−21.4 21.5−21.9	18.2 18.7 19.2 19.7 20.2 20.7 21.2 21.7	5 8 30 x=13 10 20 10 4	91 149.6 576 256.1 202 414 212 86.8	5 13 43 56 66 86 96 100
       		100	1987.5

    3. Mean = Σfx/Σf=    1987.5   
                                    100
       =19.875
    4. 19.45+ (50-43) x 0.5
                         13
       =19.45+10.26923 =19.72
20.     
    1. Diagram (Next page)
    2. 16.5x300=4950 ±30km
    3. 16x300=4800 ±30km
    4. 316° ± 1°
       
21.            
    1. Plotting PQR
    2. On grid (Triangle P'Q'R'under enlargement S.F = ½ about(2,2) )
       P'(1,1) Q'(4,1) R'(2,3)
    3. On the grid (TriangleP''Q''R'' under positive quarter turn about(1,1) )
    4. On grid (Triangle P'''Q'''R''' under reflection in the line y=1 )
    5. Reflection in the line y=−x+ 2
       
22.       
    1. Determinant = 8−9=−1
       A^-1 = 1/-1 (2 -3 -3 4) = (-2 3 3 -4)
       1. Equations:
          20x+15y = 9500
          15x+10y = 6750
       2. Solving the equations:
          20x+15y= 9500
          15x + 10y = 6750
          4x + 3y = 1900
          3x + 2y = 1350
          (4 33 2)(x y)= (1900 1350)
          (-2 3 3 -1 )(1900 1350)
          (x y )= (250 300)
          ⸫ x = Kshs 250 y = Kshs 300
       3. Oranges new price = 110/100 x 250 = Kshs.275
          Mangoes new price =90/100  x 300 = Kshs.270
          (20 15 15 10) (275 270) = 9550 6825
          total cost = 9550 + 6825 = Kshs.16
23.                 
    1.    
       

       x	-1	0	1	2	3	4	5
       y	7	2	-1	-2	-1	2	7

          
    2. Curve
       1.  
               
       2. Line drawn
    3. x = 0.7 or 4.3 ± 0.1
    4. x = 2
24.    
    1. ds/dt =12t² −5t −3
       v =12t² −5t −3 v =12(3)²
       −5(3)−3 v = 90m/s
    2. 12t2 −5t −3=0
       12t2 −9t + 4t −3 = 0
       3t(4t −3)+1(4t −3)= 0
       (4t −3)(3t +1)= 0
       t = 3/4 or 1/3
       t = 3/4 seconds
    3. Displacement at t =
       s = 4t³ − 5/2 t² −3t+3
       s = 3/4
       s = 4(3/4)³ - (3/4)² - 3(3/4) + 3
       s =³³/₃₂ = 1 ¹/₃₂ or 1.03125
    4. a= dvdy =24t – 5
       a =dvdy =24(2)-5
       a = 43 m/s²