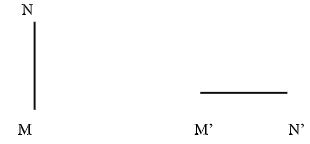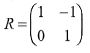Mathematics Paper 1 Questions - Bondo Joint Mocks Exams 2022

Questions

Instructions to candidates

• This paper contains two sections: Section I and Section II. Attempt all the questions in section I and strictly any five questions from Section II.
• All answers and working must be written on the question paper in the spaces provided below each question.
• Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
• Marks may be given for correct working even if the answer is wrong.
• Non-programmable silent electronic calculators and KNEC mathematical tables may be used, except where stated otherwise.

SECTION A (50 MARKS)
Attempt ALL questions in this section

1. Use logarithms table to evaluate (3marks)
2. In blessed church choir, the ratio of males to females is 2:3, on one Sunday service, ten males members were absent and six new female members joined the choir as guests for the day. If on this day the ratio of males to females was 1:3, how many regular members does the choir have? (3marks)
3. Evaluate without using tables or calculators. (2marks)
   (3√729)2 X (4√16)3 ÷ (5√243)
4. Three tellers in a bank can each serve a customer in 42seconds, 56secs and 84secs respectively. Determine the shortest time they can take to serve a total of 117 customers. (4marks)
5. Simplify the expression (2marks)
     x -1   -    2x - 1  
     x               3x
   Hence solve the equation (2marks)
     x - 1   -    2x - 1   =       2     
        x               3x            3
6. A tourist exchanged X Us dollars for Kenya shillings when he arrived in Kenya. He spent three days in the country and paid Kshs 45,600 for expenses. He later left country and exchanged the remainder back to US dollars. He went back with 1200 dollars. Given that
   Buying 1 US dollars =Kshs 98.36
   Selling 1 US dollar =Kshs 98.54
   Find the value of x to the nearest dollar. (3marks)
7. Determine the radius of a uniform cylindrical block. 1.4m long and of density of 2.2g/cm 3 . If the mass is 47432g.(Use = ) (3marks)
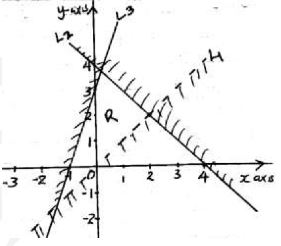
8. Write down the three inequalities which define the region R (3marks)
   
9. Without using tables, evaluate and give your answer in standard form  (3 marks)
       0.51  x  5700   
        6.8  x  0.0095
10. Points A(-2,2) and B(-3,7) are mapped onto A 1 (4,-10) and B 1 (0,10) by an enlargement . Find the scale factor of the enlargement. (3 marks)
11. The diagram below shows a line NM and its image N´M´ after a rotation. Determine, by construction, the centre of the rotation O and angle of the rotation. (3 marks)
    
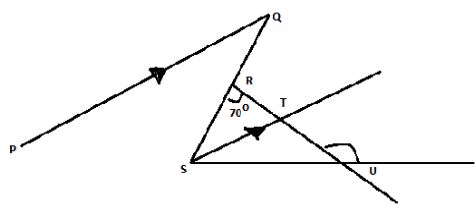
12. In the figure below PQ is parallel to ST and ST bisects angle. QSV. Angle SRU=70 o while angle RUV=120 o If S, U and V are points in a straight line.
    Giving reasons, find:
    
    
    1. Angle RSV (2marks)
    2. Angle PQS (2marks)
13. Factorise and simplify completely the fractional expression (3 marks)
    2my +xy -y² - 2mx
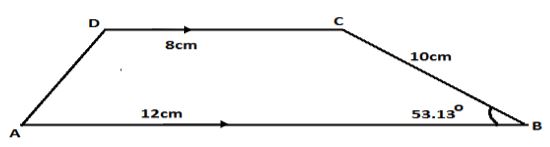
        y² - 4m²
14. The figure below shows a trapezium ABCD in which AB is parallel to CD and angle ABC=53.13° , AB=12cm, BC =10cm and CD=8cm. calculate the area of the trapezium. (3 marks)
    
15. Line L₁ has equation ¹/₂x-y=3. If L 1 passes through the point (R(8,n), find the value of n and hence the equation of the L₂ which makes an angle of 135° with the x-axis and passing through R (3 marks)
16. Using trapezium rule with 5 ordinates, approximate the area bounded by the curve y = -x² + ¼ , x= -3, x=5 and the x-axis (3 marks)

SECTION B: (50MARKS):
Attempt only five questions from this section

17.      
    1. Complete the table below for the graph y=6 + x - x 2 for -2 ≤ x ≤ 4 (2 marks)
       

       x	-2	-1	0	1	2	3	4
       y	0		6			0

    2. Draw the graph of y=6 + x - x² for -2 ≤ x ≤ 4. Use scale of 2cm to represent 1 unit on x –axis and 1cm to represent 1 unit on y-axis (3 marks)
    3. Use your graph to solve the equation
       1. x² -3x -4 =0 (3 marks)
       2. 6 + x - x² < 1 (2 marks)
18.   
    1. A triangle ABC, A(0,1), B(3,0) and C(1,3) is mapped onto triangle A 1 B 1 C 1 by matrix 
       
       Write down the co-ordinates for triangle A¹B¹C¹ (3 marks)
    2. Triangle A¹¹B¹¹C¹¹ is the image of A¹B¹C¹ under transformation represented by matrix
       Write down the co-ordinates for triangle A 11 B 11 C 11 (3 marks)
    3. Find a single matrix represented by R followed by Q (2 marks)
    4. A square PQRS whose coordinates are P(0,0) Q(4,0) R(4,4) and S(0,4) Under a shear matrix with x-axis invariant, R(4,4) is mapped onto R¹(-8,4) Determine the shear matrix (2 marks)
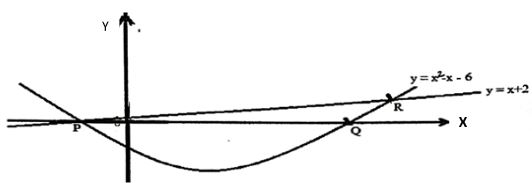
19. The figure below shows a circle whose equation is y=x ² – x - 6 intersecting a straight line whose equation is y= x+2 at points P and R. Point P and Q are x-intersects for the curve.
    
    
    1. Determine the co-ordinates of points P and R (3 marks)
    2. Calculate the area bounded by the curve y=x² - x - 6, and the x-axis between P and Q (3 marks)
    3. Calculate the exact area bounded by the curve y=x² - x - 6 and the lines y = x+2 (4 marks)
       
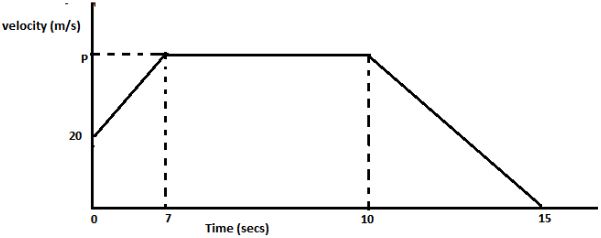
20. The diagram below shows a velocity time graph of a car that accelerated uniformly from 20m/s to attain a maximum speed P m/s in 7 seconds. It then maintained the speed P m/s for another 3 seconds before decelerating to rest in a further 5 seconds.
    Given the average speed of the car for the whole journey is 25 2 / 3 m/s .
    1. Calculate the value of P (5 marks)
    2. Determine the time taken to cover the first three fifths of the whole of the journey (3 marks)
    3. Calculate the speed of the car on the 13 th second of motion (2 marks)
21.  
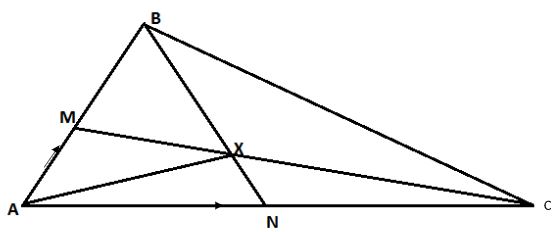
    1. In triangle. ABC shown below, AB=a AC=b. Point M lies on AB such that AM:MB=2:3 and point N lies on AC such that AC:CN =6:-1.BN intersect line MC at X
       
       Express the following interns of a and b
       1. BN (1mark)
       2. CM (1 mark)
    2. Given that BX=kBN and CN = rCM where k and r are scalars, write down two different expressions for AX in terms of a,b k and r hence find values of k and r. (8 marks)
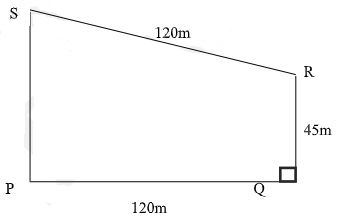
22. The diagram below shows a quadrilateral garden in which PQ=120m ,QR=45m,RS=120 m and angle QRS=135° while angle PQR=90°
    
    
    1. Calculate to 1 decimal place
       1. The size of angle QPR (2 marks)
       2. The length PS (4 marks)
    2. The area of the garden in hectares correct to 2 significant figures (4 marks)
23. An expedition has 5 sections AB, BC CD DF and EA. B is 200m on a bearing of 050° from A. C is 500km from B. The bearing of B from C is 300° . D is 400km on a bearing of 230° from C, and E is 250m on a bearing of 025° from D
    1. Sketch the route (1 mark)
    2. Use the scale of 1cm represent 50m to draw the accurate diagram representing the route (6 marks)
    3. Use your diagram to determine
       1. Distance of A from E (2 marks)
       2. Bearing of E from A (1 mark)
24. The figure below shows two circles, center P and Q. AP=5.4cm, AQ=7.8cm and PQ =11.5cm. AC meet PQ at M
    Calculate
    1. < APM (2 marks)
    2. Length AM (2 marks)
    3. The area of the shaded region (6 marks)