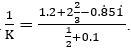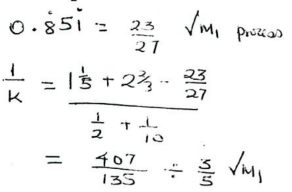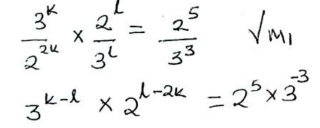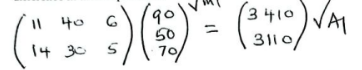Mathematics Paper 1 Questions and Answers - Maranda High School Mock Exams 2023

Share via Whatsapp

Next Topic »
Mathematics Paper 2 Questions and Answers - Maranda High School Mock Exams 2023

Download PDF for future reference Get on Whatsapp for 50/-

Instructions to candidates

This paper consists of two sections: Section I and Section II.
Answer all the questions in Section I and only five questions from Section II.
Show all the steps in your calculations, giving your answers at each stage in the spaces provided below each question.
Marks may be given for correct working even if the answer is wrong.
Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.
Candidates should answer the questions in English

SECTION I (50 marks)

Answer all the questions in this section in the spaces provided:

Simplify the expression {2(−x+3y) −0.5 (2x−y)}. (2 marks)
Solve for K in the equation (4 marks)
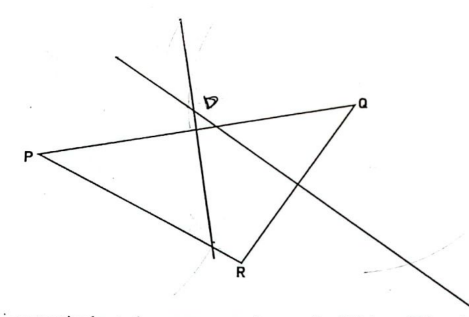
The scale diagram below shows the relative positions of three towns P, Q and R drawn to a scale of 1:100,000.

By construction locate the common sercurity camp D which is equididtant from three towns hence state its distance from town P. (3 marks)
Given that matrix A = is a singular matrix solve for m. (2 marks)
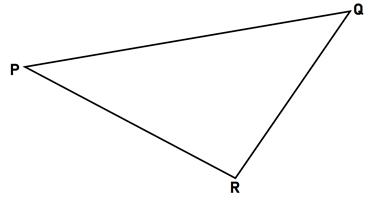
The figure shows triangle ABC and x and y are two exterior angles and angle ABC=nº.

Given that x+y=220° calculate the value of n. (3 marks)
Solve for k and l in the equation(³/₄)^k × (²/₃)^L = ³²/₂₇. (4 marks)
Mama Mboga added a stock of tomatoes to her stall. She tried grouping the tomatoes into piles of either 3 tomatoes, 4 tomatoes or 5 tomatoes before selling and realized that when piled in 3s she remained with 1 tomato while when she puts them into the piles of 4 tomatoes 2 remained in her basket and 3 tomatoes when distributed in piles of 5 tomatoes. Determine how much more she could have if she finally chose to sell them in piles of 3s istead of 5s if each pile of 5 was to be sold at Kshs.45 and Kshs.30 for piles of 3s and the remainder in each case she took to for her personal consumption.
(4 marks)
Evaluate 16^x given that x and y are positive integers and 2x − 4y = 3. (2 marks)
256^y
The figure below is a square in which arcs of radius 3cm each have been made from its corners as shown.

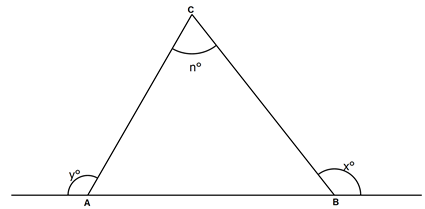
Calculate the area of the shaded region leaving your answer in terms of π. (2 marks)
The figure below is a velocity time graph for a car.

Calculate the maximum velocity attained by the car if covered a distance of 270m within the first 20s of its journey. (2 marks)
Mercy spent a total of Ksh. 196 on buying 3 exercise books and 5 pens. If she could have bought 2 exercise books and 8 pens, she could have spent Ksh. 28 more. Taking Ksh. x to be the cost of one exercise book and Ksh. y to be the cost of each pen use the grid provided to solve for x and y.
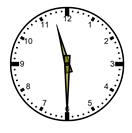
(4 marks) (Use 1cm to represent Ksh. 5 in both axes)
The figure below shows the correct time when Peter set his faulty watch on a Monday morning.

Determine the time, in 24 hour clock system, it showed at noon Friday the following week if it looses 4 seconds every hour. (4 marks)
The graph below shows a section of a curve y = ax² + bx + c

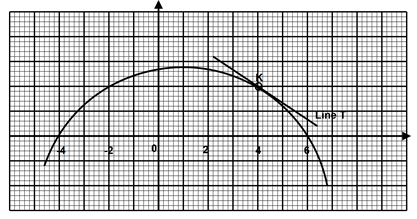
Given that the line T is a tangent to the curve at point K determine its equation. (4 marks)
After selling a bag of potatoes at Sh. 420 Paul made some profit. If he could have sold it at Sh. 320 he could have made a loss. Given that the profit is thrice the loss calculate the amount of money he paid for the bag of potatoes. (3 marks)
After planning to buy a certain number of cartons of a fruit juice for a total of KShs.30,000 the price of each carton was lowered by KShs.100 and this enabled an hotelier to purchase 10 more cartons of the juice. Determine the original number of cartons of juice he planned to purchase. (4 marks)
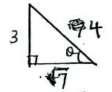
Without using calculator or mathematical table evaluate sin⁡(90−θ)°tan⁡(90−θ)° given that cosθ = ^√7/₄. (3 marks)

SECTION II (50 marks)

Answer any five questions from this section

A line L1 with equation –px + 2y = 3 passes through the point (−3,1). Calculate:
1. the value of p (2 marks)
2. the size of the obtuse angle which line L₁ makes with x-axis (4 marks)
3. the equation of line L₂ parallel to L₁ and passes through (2,6) in form of y=mx +c. (2 marks)
4. the equation of the line L₃ perpendicular to L1 at (−3,1). Give your answer in the form ax + by = c. (2 marks)
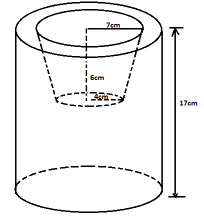
The figure below shows a traditional artifact made of wood. It consist of outer cylindrical surface radius 9cm and a frustum of the top radius 7cm and bottom radius 4cm, height 6cm (Take π = ²²/₇)
1. The surface of the model is to be painted including the inner frustum surface. Determine the total area painted to 2 decimal places (6 marks)
2. Calculate the volume of wood used to the model (4 marks)
Below is a histogram showing the performance of a class in an internal Maths Contest .
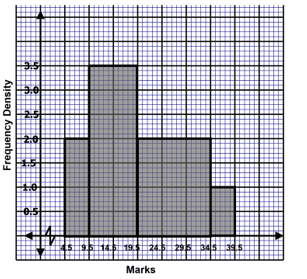
1. If the frequency of the first class is 10, develop a frequency distribution table from the histogram above. (3 marks)
  
  Marks Frequency
  
  5-9 10
2. State the modal class (1 mark)
3. Use the histogram above to determine:-
  1. The median mark to four significant figures. (3 marks)
  2. The mean mark (3 marks)
Onyango and Wairimu bought some items from hardware. Onyango bought 11 bags of cement, 40 Iron sheets and 6 litres of paint while Wairimu bought 14 bags of cement, 30 Iron sheets and 5 litres of paint. The prices of a bag of cement, a piece of iron sheet and a litre of paint were sold for Ksh. 90, Ksh.50 and Ksh.70 respectively.
1. Represent:
  1. The number of items bought by Onyango and Wairimu using 2 x 3 matrix. (1 mark)
  2. The price of the item bought using 3x1 matrix. (1 mark)
2. Using the matrices in (a) above to determine the total expenditure incurred by each person hence the difference in their expenditure. (3 marks)
3. Amani and Wafula also bought bags of cement and Iron sheets. Amani bought 36 bags of cement and 23 iron sheets and paid Ksh. 8,160 while Wafula bought 50 bags of cement and 32 Iron sheet and paid Ksh. 11,340. Use the matrix method to determine the price of a bag of cement and apiece of Iron sheets. (5 marks)
The displacement, s metres, of a moving particle after t seconds is given by
S = t³ + 6t² − 9t + 5
Determine:
1. The velocity of the particle when t = 2seconds (3 marks)
2. The value of t when the particle is momentarily at rest. (3 marks)
3. The displacement when the particle is monetarily at rest. (2 marks)
4. The acceleration of the particle when t = 4seconds (2 marks)
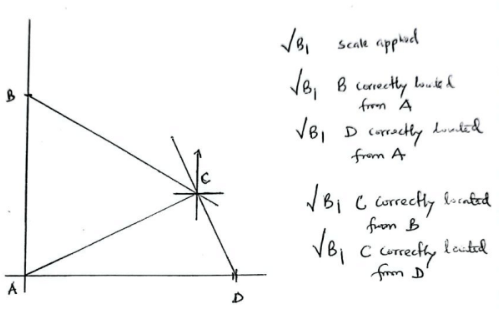
Four pegs A, B, C and D are on the vertices of a plain field. B is 360 m north of A and D is 420 m east of A. The bearing of C from B is 120° and the bearing of D from C is S25°E.
1. Using a scale of 1 cm to represent 60 m, represent the information on a scale drawing. (5 marks)
2. Using the scale drawing, determine
  1. Compass bearing of C from A. (1 mark)
  2. The distance between C and D. (1 mark)
  3. The perimeter of the region enclosed by the four pegs. (3 marks)
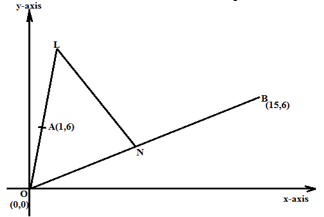
In the diagram below, the coordinates of points A and B are (1, 6) and (15, 6) respectively). Point N is on OB such that OB: BN = 3:−1. Line OA is produced to L such that ¹/₃OL = OA
1. Find vector LN (2 marks)
2. Given that a point M is on LN such that LM: MN = 3: 4, find the coordinates of M. (3 marks)
3. If line OM is produced to T such that OM: MT = 6:1
  1. Find the position vector of T (2 marks)
  2. Show that points L, T and B are collinear (3 marks)
1. On the grid, plot triangle ABC in which A (2,1), B(1,5) and C(5,2) (1 mark)
2. Rotate ABC to A' B' C' through +90 about (0,0) and state the coordinates of A' B' C'. (2 marks)
3. Reflect A' B'C' to A'' B''C'' in the line line y − x = 0. (2 marks)
4. Find the image of A'' B''C'' under enlargement scale factor −2 about (0,0) hence state the coordinates A''' B'''C'''. (2 marks)
5. State pairs of triangles above that are:
  1. oppositely congruent. (2 marks)
  2. directly congruent . (1 mark)

MARKING SCHEME

= {−2x + 6y − x + 0.5y} M1
= − 3x + 6.5y A1
=⁴⁰⁷/₁₃₅ × ⁵/₃
K = ⁸¹/₄₀₇
- B1 Bisecting any two sides
- B1 Location of D
- B1 4.5 ± 0.1km
−2m + 0.5 = 0
m = 0.25
(180 − y)° + (180 − x)° + n° = 180° ✓M1
360 + n − (x+y) = 180° ✓M1 Substitution for (x+y)
n − 220° = − 180°
n = 40° ✓A1
k − l = −3
l − 2k = 5   ✓ M1
−k = 2    ✓M1
−2 − l = − 3
l = 1   ✓A1
Common differences = 5  − 3 = 4  − 2 = 3 − 1
= 2
LCM = 5 × 4 × 3   ✓M1
= 60
No. of tomatoes = 60 − 2 ✓M1
= 58
58/5 = 11³/₅ piles and ⁵⁸/₃ = 19¹/₃piles
Difference = (19×30) − (45×11)  ✓M1
= 75/= ✓A1
16^x = 4^2x
256^y 4^4y
= 4^{2x − 4y} ✓M1
=4³
= 64 ✓A1
Area = 6² − 4 × ¼π × 3² ✓M1
= 36 − 9π ✓A1
½ × 4 × V_max + 16 × V_max = 270 ✓M1
18 V_Max = 270
V_max = 15ms⁻¹ ✓A1
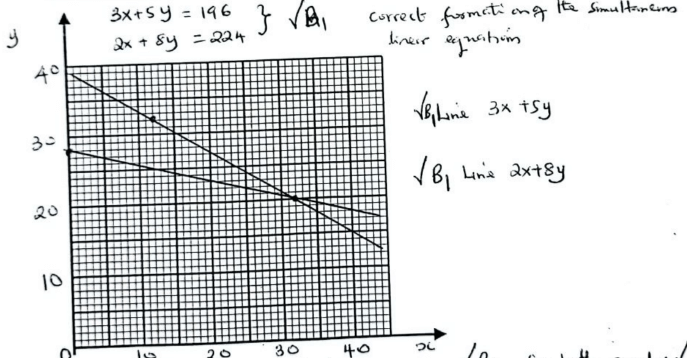
x = 32/= y = 20/= ✓B1 for both x and y
Time = 11:30am Monday ✓B1
From Monday h11:30am to Friday Noon the following week
= (12 × 24)hrs + 30mins ✓M1
= 288½hours
Time lost = 288½ × 4 ✓M1
60
= 19mins 14 seconds
Time in the watch
= 11:40:46am ✓A1
At y = 0 x = −4 or 6
(x+4) (x − 6) = 0 vM1
x₂ − 2x −24 = 0
The curving is maximum hence
y = −x² + 2x ,+ 24
At maximum ^dy/_dx = −2x + 2 ✓M1
Gradient = −2 × 4 + 2
= − 6
At x = 4 y = 16 hence k (4,16) is
− 6 = y − 16 ✓M1
x − 6
y = − 6x + 40 ✓A1
P = 420 − B.P
L = B.P − 320
But L = ¹/₃P
P = 420 − B.P
¹/₃P = B.P − 320 ✓M1
^h/₃P = 100 ✓M1
P = 75/=
B.P = 420 − 75 ✓M1
= 345/= ✓A1
Let the original number of cartons be X
30000  − 30000 = 100 ✓M1
x x + 10
100x² + 1000x − 300000 = 0   ✓M1
x2 + 10x − 3000 =
(x − 50) (x+60) = 0   ✓M1
x = 50 or −60
x = 50 cartons ✓A1
Sin (90 − θ)° = ^√7/₄ ✓M1
Tan (90 − θ)° = ^√7/₃ ✓M1
Sin(90 − θ)° Tan (90 − θ)°
=^√7/₄ ×^√7/₃
=⁷/₁₂ ✓A1
1. −P (−3) + 2(1) = 3 ✓M1
  P = ¹/₃
2. ¹/₃x + 2y = 3
  2y = −¹/₃x + 3
  y = −¹/₆x + ³/₂ ✓M1
  tan θ = (−¹/₆) ✓M1
  ⇒ θ° = 9.46°
  But θ is obtuse
  θ° = 180° − 9.46° ✓M1
  = 170.54° ✓A1
3. −1/6 = y − 6 ✓M1
  x − 2
  6y − 36 = −x + 2
  y = − ¹/₆x + 6¹/₃ ✓A1
4. −¹/₆m₂ = −1 ⇒ m₂ = 6
  6 = y − 1 ✓M1
  x + 3
  6x − y = 19 ✓A1
1. ⁷/₄ = 6 − x   ✓M1
  x
  x = 3
  L = √(7² + 9²)  ✓M1
  = 11.40
  L = √(4² + 3²)
  = 5
  Total Surface Area  ✓M1
  = ²²/₇ × 9 × 9 + 2 × ²²/₇ × 9 × 7 + ²²/₇ (9² − 7²) + ²²/₇ × 4² +²²/₇ × (7 × 11.4) − (4 × 5)
  = 254.571 + 961.714 + 100.571 + 50.286 + 18.7943
  = 1555.09cm² ✓A1
2. V =²²/₇ × 9²× 17 ✓M1 − ¹/₃ { (²²/₇ (7² × 9²) − (4² × 3)} ✓M1
  = 4327.714 − 411.714 ✓M1
  = 3916 ✓A1
1. Marks Frequency
  
  5 - 9 10
  
  10 - 19 35
  
  20 - 34 30
  
  35 - 39 5
2. 10 - 19 ✓B1
3. 1. Total Area = (5×2) + (10 × 3.5) + (15×2) + (5×1) M1
    = 80
    ½A = 40
    Median = 9.5 + 40 − 10 ✓M1
    3.5
    = 18.07 ✓A1
  2. x̄ = 70 + 507.5 + 810 + 185 ✓M1 ✓m1
    80
    = 19.65625 ✓A1
2. Difference in expenditure = 3410 − 3110
  = 300
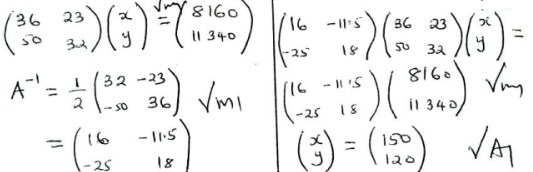
3. Cost of a bag of cement = 150/=
  Cost of a piece of iron sheet = 120/=
1. v = ^ds/_dt = 3t² + 12t − 9 ✓M1
  V(2) = 3(2)² + 12 × 2 − 9 ✓M1
  = 27ms⁻¹ ✓A1
2. At rest = ^ds/_dt = 0
  3t² + 12t − 9 = 0   ✓M1
  t + 4t − 3 = 0
  (t + 1) (t − 3) = 0   ✓M1
  t = −1 or 3
  ∴ t = 3 seconds   ✓A1
3. S = 3³ + 6(3)² − 9(3) + 5 ✓M1
  = 59
4. a = ^dv/_dt = 6t + 12 ✓M1
  a(4) = 6(4) = 12
  = 36ms⁻² ✓A1
2. 1. N25°E ✓B1
  2. 180 ± 6m ✓B1
  3. 420 + 360 + 180 + 390 ✓M1 ✓B1 for BC = 390m
    = 1350m ✓A1
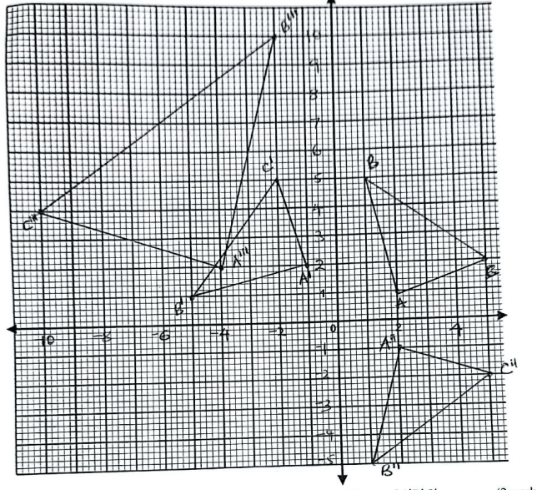
2. A'(−1,2) B'(−5,1) C'(−2,5) ✓B1 Diagram carefully plotted ✓B1 Correct coordinates
3. ✓B1 line y − x = 0 Correctly identified
  ✓B1 A''B''C'' correctly drawn
4. ✓B1 Enlargment correctly done.
5. 1. ABC and A''B''C'' ✓B1
    A'B'C' and A''B''C'' ✓B1
  2. ABC and A'B'C' ✓B1