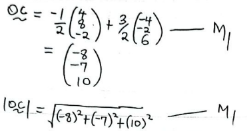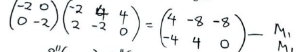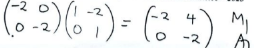Mathematics Paper 2 Questions and Answers - Maranda High School Mock Exams 2023

Instructions to Candidates

• This paper consists of two sections; Section I and Section II.
• Answer all qUestions in Section I and only five qUestions from Section II.
• Show all the steps in your calculations, giving the answers at each stage in the spaces provided below each question.
• Marks may be given for correct w rking even if he answer is wrong.
• Non-programmable silent electronic calcUlators and KNEC mathematical tables may be used, except where stated otherwise.
• Candidates should answer the questions in English.

SECTION I(50 marks)

Answer all the questions in this section in the spaces provided.

1. In calculating the volume of a cone a student had an error of 0.1% in , 0.3% in the height and 0.4% in the radius, calculate the relative error involved in calculating the volume of the cone. (3 marks)
2. Solve for in x the equation (3 marks)
   ¹/₂ log₂81 + log₂(x² − ^x/₃) = 1
3. The length of a rectangle is three times its breadth. If the breadth is decreased by 2m and the length increased by 4m, the area of the rectangle is decreased by a third. Find the area of the original rectangle. (3 marks)
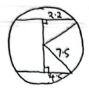
4. Two parallel chords of length 4.4 cm and 9 cm are in a circle of radius 7.5cm. Calculate the distance between the two chords given that they are on different sides of the centre. (3 marks)
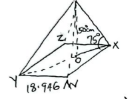
5. A square based pyramid has a height 50cm.The sloping edges make an angle of 75° with the base. Find the volume of the pyramid. (3 marks)
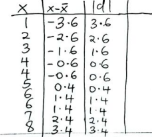
6. Calculate the mean absolute deviation of the set of data below:
   1, 6, 4, 7, 3, 8, 4, 6, 5, 2. (3 marks)
7.                                            →                               →                                                                                                                 →
   Given the position vectors OA = 4i + 8j − 2k and OB = 6k − 4i − 2j . Point C divides in the ratio of  3: −1. Find the modulus OC of Give your answer to 2 d.p. (3 marks)
8. Below is a circle centre O.
   
   Find the equation of the circle in the form ax² + by² + cx + dy + e = 0 where a, b, c, d and e are integers. (3 marks)
9. Tractor A can plough a peace of land in 4½ hours while tractor B can do the same amount of work in 7½ hours. Both tractors began to plough the piece of land but after 2 hours tractor A broke down and B had to clear the remaining work. The two tractors are operated by different owners. The whole work was valued at Ksh.13 500 and was shared proportionally to work done. Calculate the amount of money received by the owner of tractor B. (4 marks)
10. The gradient of the curve y = 2x² + c at the point (p, 5) equals −8. Find the values of p and c. (3 marks)
11. A theatre is designed so that the next row of seats has d less seats than the row behind. The first row has a seats while the tenth row has 435 seats. There are 25 rows of seats in all. The entire theatre contains 9000 seats. Find the values of a and d. (3 marks)
12. Find the value of if  (4 marks)
13. The figure below shows part of the a curve which passes through point A (3,8)
    
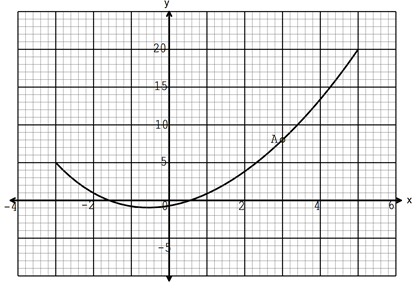
    Determine the instantaneous rate of change at A. (3 marks)
14. Pascal earned an interest of Ksh 2 122 312 after seven years on an investment project which paid 13% per annum interest compounded semi-annually. Find the amount Pascal invested to the nearest thousand (3 marks)
15. The rate of growth of a great white shark, ^dl/_dt ,is inversely proportional to the square root of its age, t years. When a shark is four years old, its growth rate is 0.14m/year. A newborn shark is 1.2m long. Determine the length of a 25- year old shark. (3 marks)
16. The figure below represents the curve of the function y = 1 = P sin dx for the range −25° ≤ x ≤ 55°
    
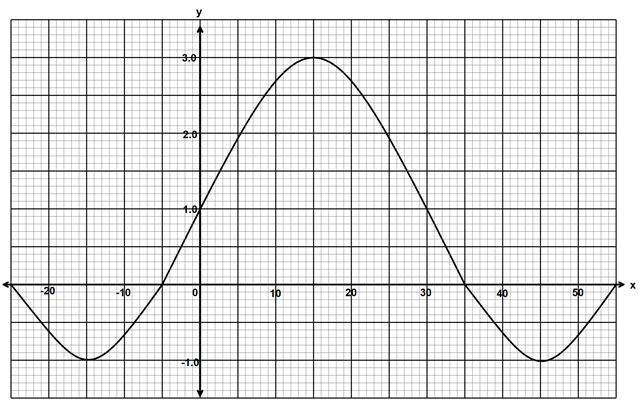
    Determine the values of P and d             (3 marks)

SECTION II (50 MARKS)

Answer ANY FIVE Questions from this Section

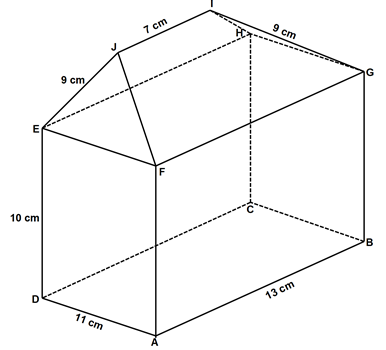
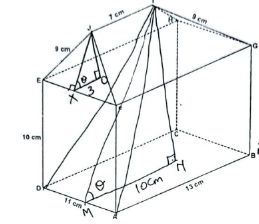
17. The figure below shows a model of a house, with a hip top EFGHIJ as its roof. The edge IJ = 7 cm is centrally placed above the plane EFGH. Given that AB = 13 cm, AD = 11 cm, DE = 10 cm and EJ = FJ = HI = GI = 9 cm.
    
    Calculate to two decimal places
    1. The length EB. (2 marks)
    2. The angle that line EB makes with the plane ABCD. (2 marks)
    3. The angle between plane JEF and plane ABCD. (2 marks)
    4. The angle between plane ADI and plane ABCD. (4 marks)
18. The figure below shows triangle PQR and its image P'Q'R' under a transformation matrix T
    
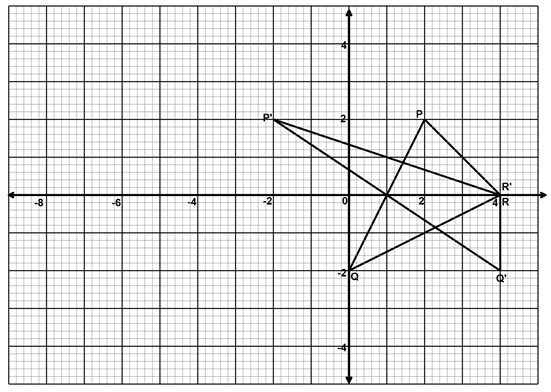
    1. Determine the matrix of transformation that maps triangle PQR onto triangle P'Q'R'.     (3 marks)
    2. Describe the transformation T fully. (2 marks)
    3. Triangle P'Q'R' is mapped onto triangle P''Q''R'' by a transformation defined by the matrix 
       1. Draw triangle P''Q''R'' on the same grid (3 marks)
       2. Find a single matrix that maps triangle PQR onto triangle P''Q''R'' (2 marks)
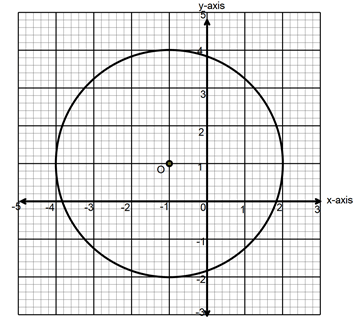
19. The figure below shows a semi-circle centre (5,0) and radius 5 units.
    
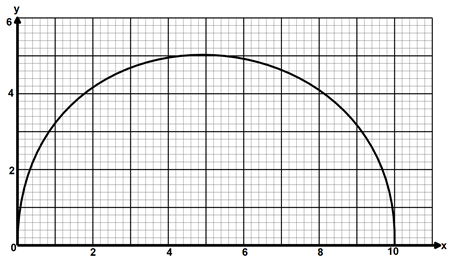
    1. Estimate the area of the semi-circle using:
       1. Trapezoidal rule with 5 strips (4 marks)
       2. Mid –ordinate rule with 5 rectangles (4 marks)
    2. Find in terms of π, the percentage error in the area of the semi-circle when mid-ordinate rule is used as in (a)(ii) above. (2 marks)
20. Mairura has to transport 42 tonnes of potatoes to the market in a day. A lorry and a trailer are available. The lorry can carry 4 tonnes of potatoes per trip while the trailer carries 6 tonnes of potatoes per trip. A lorry uses 2 litres of fuel per trip while a trailer uses 4 litres of fuel per trip. The two vehicles are to use less than 24 litres of fuel. The number of trips made by the lorry should be less than the number of trips made by the trailer. The lorry should make more than 4 trips.
    1. Taking x and y to represent the number of trips made by lorry and trailer respectively, write the inequalities that represent the above information.
       (4 marks)
    2. On the grid provided, plot the inequalities in (a) above. (4 marks)
       
    3. If a lorry makes a profit of Ksh 35 000 per trip and a trailer makes a profit Ksh.28 000 per trip, using a search line or otherwise, determine the maximum profit made by Mairura (2 marks)
21. Bag A contains 4 red balls and 5 white balls while bag B contains 6 red balls and 4 white ones.
    1. A bag is picked at random and a ball is picked, find the probability that the ball is white.     (2 marks)
    2. A ball is removed from A and placed in bag B. Two balls are then picked from B at random one at a time without replacement; find the probability that the two balls are of the same colour. (4 marks)
    3. Three boys and three girls sit in a row of six seats. Find the probability that:-
       1. Three girls sit together. (2 marks)
       2. The girls and boys sit in alternative seats. (2 marks)
22.  
    1. A point Q is 2610nm to the east of P(0°, 155°E). Find the longitude of Q. (3 marks)
    2. The position of three cities are A(15°N, 20°W ), B(50°N, 20°W ) and R(50°N, 60°E). A plane left city A at 0250hrs and flew to city B at where it stopped for 3hours then flew on to city C, maintaining a speed of 900 knots through-out. Calculate;
       1. the total distance covered by the plane from city A to R via C. ( 3 marks)
       2. the local time(to the nearest minute) at city R when the plane arrived. (4 marks)
23. The table below shows income tax in a certain year.
    

    Monthly taxable income in Ksh.	Tax rates
    0 - 12 298	10%
    12 299 - 23 885	15%
    23 886 - 35 472	20%
    35 473 - 47 059	25%
    47 060 and above	30%

    In that year, Kamau earned a basic salary of Ksh.45,000 per month. He also enjoyed the following allowances. House allowance Ksh.35 000, Commuter allowance Ksh.10 000, Medical allowance Ksh 15 000. He has an insurance scheme for which he pays a monthly premium of Ksh.22 000. He is therefore entitled to a relief of 15% of the premium paid. He contributes 10% of his basic salary to a pension scheme, which is exempted from taxation. He was entitled to a personal relief of Ksh.1 280 per month.
    Calculate;
    1. Kamau’s monthly taxable income. (2 marks)
    2. The tax payable by Kamau that month. (5 marks)
    3. The following deductions are also made from Kamau’s salary every month.
       1. N.H.I.F of Ksh.320
       2. Cooperative society shares of Ksh.6 000
       3. Union dues of Ksh.200.
          Calculate Kamau’s net monthly salary (3 marks)
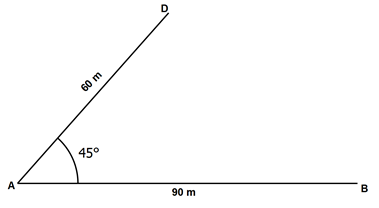
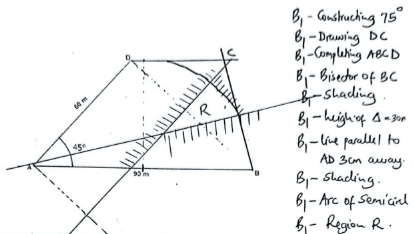
24. The figure below shows the edges AB = 90m and AC = 60m of a trapezoidal field ABCD drawn to scale. Angle DAB = 45°.
    
    Using a ruler and a pair of compasses only;
    1. Complete trapezium ABCD such that angle ABD = 75◦ (3 marks)
    2. Locate by construction a region R within the trapezium and on the same side of AB as CD which satisfy the conditions below.
       1. R is such that BR ≥ CR (2 marks)
       2. the area of triangle ARD is at least 450m² (3 marks)
       3. R such that angle ARB is at least 90° (2 marks)

MARKING SCHEME

1. V = ¹/₃πr²h
       = 0.1 + 290.4) + 0.3  ✓M1
      = 1.1%
   Relative error = ^1.1/₁₀₀   ✓M1
                          = 0.011  ✓A1
2. 9(x² − ^x/₃) =2    ✓M1
   9x² − 3x −  2 = 0
   x = 3±√{9−4(9x−2)}     ✓M1
                    18
   x = ²/₃ or −¹/₃       ✓A1
3. Length = 3x
   Width = x
   (3x + 4) (x−2) = ²/₃(3x²)    ✓M1
   x² − 2x − 8 = 0
   (x + 2)  (x − 4) = 0   ✓M1
   x = −2 or 4
   area = 3(4)²
            = 48m²    ✓ A1
4.  
    
   √(7.5² − 2.2²)  ✓M1+ √(7.5² − 4.5²) ✓M1
   7.17cm + 6cm
   13.17cm   A1
5. 
   
   OX =    50        ✓M1
            tan 75°
   XY = 2 ×    50     
                  tan 75°
         = 26.795cm
   V = ¹/₃ × ¹/₂ × 26.795 × 50        ✓M1   
       = 5983.1cm³    ✓A1
6.  
   
   X̄ = ⁴⁶/₁₀ = 4.6     ✓M1
     = Σldl        
          N
     = ¹⁸/₁₀      ✓M1
    = 1.8      ✓A1
7.  
   
          = 14.59 units       ✓A1
8. Centre (−1,1)
   Radius = 3 units
   (x+1)² + (y−1)² = 9    ✓M1
   x² + 2x + 1 + y² − 2y + 1 = 9
   x² + y² + 2x − 2y − 7 = 0    ✓A1
9. Work done by A = ¹/_4½ × 2
                              = ⁴/₉          ✓M1
   Work done by B = 1 − ⁴/₉ = ⁵/₉       ✓M1
   Amount = ⁵/₉ × 13,500      ✓M1
               = Ksh. 7500     ✓A1
10. ^dy/_dx = 4x
    4p = −8   ✓M1
      p = −2
    5 = 2(−2)² + c  ✓M1
    c = −3  ✓A1
11. a + 9d = 435 ..........(i)
    ²⁵/₂[2a+d(25−1)] = 9000   ✓M1
    2a + 24d = 720.........(ii)
    2a + 18d = 870
    2a + 24d = 720    ✓M1
            −6d = 150
         d = −25
         a = 660       ✓A1   
12.  
      ✓M1 - for integration
    (9 + 12 + c) − (a² + 4a + c) = 25     ✓M1
    a² + 4a + 4 = 0
    a = −4±√(16−16)    ✓M1
                   2
          = − 2     ✓A1
13. B1 tangent correctly drawn
    A(3, 8)     (1.5, 0 )
    Gradient =   0 − 8       ✓M1
                      1.5 − 3     
                   = 5¹/₃    ✓A1
14. P + 2 122 312 = P (1 + ^6.5/₁₀₀)¹⁴    ✓M1"
    P + 2 122 312 = 2.4149P      ✓M1
     P = 1,500,000.511
        = Ksh 1,500,000     ✓A1
15. ^dl/_dt m= ^K/_√t
    0.14 = ^K/_√4
    K = 0.28
    ^dl/_dt = ^0.28/_√t = 0.28t^−½ ✓M1
    L = ∫ 0.28t^−½    M1
    L = 0.28t^½ + c   M1
    L = 0.56t^½ + c
    1.2 = 0.56(0)^½ + c   ✓M1
    c = 1.2m
    L = 0.56(25)^½ + 1.2   ✓M1
    = 4m   ✓A1
16. P = 3 − 1   ✓M1
        = 2 ✓A1
    ³⁶⁰/_d = 60
    d = 6
17.  
    
    
    1. DB = √(112 +132) = √290   ✓M1
       EB = √(102 + 290) = √f390 = 19.74cm  ✓ A1
    2. θ =   tan^{−1 10}/_√29   ✓M1
          = 30.42°   ✓A1
       
    3.  
       
       Jx = √(92 − 5.52) = 7.124
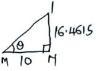
       θ = Cos⁻¹(³/_7.124) = 65.09°   A1
    4. Nl = 10 + √(7.1242− 32)
            = 10 + 6.4515
            = 16.4615
       
       θ = tan⁻¹(16.4615)  ✓ M1
                            10
          = 58.72°   ✓ A1
18.  
    
    1.  
       
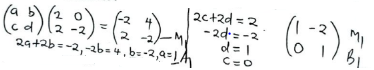
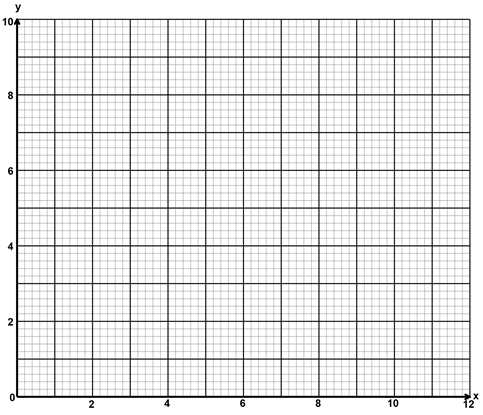
    2. Shear x - axis invariant mapping ,P(2,2) onto P'(−2,2)
    3.  
       1.  
          
          P''(4,−4) Q''(−w8,4) R''(−8,0)   ✓A1
       2.  
          
19.  
    1.  
       1. h = ¹⁰/₅ = 2
          

          x	0	2	4	6	8	10
          y	0	4.1	4.9	4.9	4.2	0

          A = ½ × [(0+0) + 2(4.1+4.9+4.9+4.1)]   ✓M1
              = 36 sq. units   ✓A1
       2. h = ¹⁰/₅ = 2
          

          x	1	3	5	7	9
          y	3.2	4.7	5	4.7	3.2

          A = 2(3.2 + 4.7 + 5 + 4.7 + 3.2)   ✓M1
              = 41.6 sq.units
    2. Exact Area = ½π×5² = 12.5π
       % age error = (13.24 − 12.5)π × 10d   
                                        12.5π  
       = 5.92%   ✓M1
       = 1.884 π%      ✓  A1
20.  
    1. x < y    ✓B1
       x + 2y< 12     ✓B1
       2x + 3y ≥ 21       ✓B1
       x > 4
       y ≤ 9     ✓B1
    2.  
       
    3. 35,000x + 28,000y = k   (9,9)    ✓B1
       35,000(9) + 28000(9) = 567,000    ✓B1
21.  
    1. P(AW) or P(BW)
       (½ ×⁵/₉) +(½×⁴/₁₀)     ✓M1
             = ⁴³/₉₀    ✓A1
    2.  
       
       (⁴/₉×⁷/₁₁×⁶/₁₀) + (⁴/₉×⁴/₁₁׳/₁₀) + (⁵/₉×⁶/₁₁)×⁵/₁₀) + (⁵/₉×⁵/₁₁×⁴/₁₀) 
       168 +  48  + 150 + 100        ✓M1
       990     990   990     990
        = 466     ✓A1
            990    
    3.  
       1. (GGGBBB) or (BGGGBB) or (BBGGGB) or (BBBGGG)
          (³/₆ײ/₅×¹/₄) + (³/₆׳/₅ײ/₄×¹/₃) + (³/₆ײ/₅׳/₄ײ/₃×¹/₂) + (³/₆ײ/₅×¹/₄)       ✓M1   
            6  +  18 + 36  +  6   
          120   360   720   120
          = ¹/₅    ✓A1
       2. (BGBGBG) or (GBGBGB)
          (³/₆׳/₅ײ/₄ײ/₃×¹/₂) +  (³/₆׳/₅ײ/₄ײ/₃×¹/₂)   ✓M1
           36  +   36    = ¹/₁₀    ✓A1
          720     720 
22.  
    1. 60θ = 2610       ✓M1
           θ = 43.5 
       longitude of Q = 360° − (155+43.5)       ✓M1
                              = 161.5°W
    2.  
       1. (35 × 60) + (80 × 60 Cos 50)
          2100 + 3085.38   ✓M1M1
          5185.38nm   ✓A1
       2. Time taken = 2100 + 3085.3805 + 3hrs
                                 900          900
                             =2¹/₃hrs + 3hrs + 3hrs 25min 41s    ✓M1
                              = 8hrs 45min 41s
          Time differnece = 80 × 4             ✓M1
                                    = 5hrs 20 min    
          02 50
            5 20  +
            8 45 41     ✓M1
          16 55 41  
           = 1655hrs     ✓A1
23.  
    1. 45,000 + 35,000 + 10,000 + 15,000 − ¹⁰/₁₀₀ × 45,000 = Ksh 100,500 ✓A1
    2. 0.1 × 12298 =   1229.80   ✓M1
       0.15 × 11587 = 1738.05
       0.2 × 11857 =    2317.4   ✓M1
       0.25 × 11857 = 2896.75
       0.3 × 53441 =  16032.3       ✓M1
                              24.214.3
       Net tax = 24 214.3 − (1280 + 3300)      ✓M1
                    = Ksh 19634.30      ✓A1
    3. Net pay = 100,500 − (19634.30 + 22000 + 320 + 6000 + 200)   ✓M1
                     = 100,500 − 48154.30        ✓M1
                    = Ksh 52345.70       ✓A1
24.