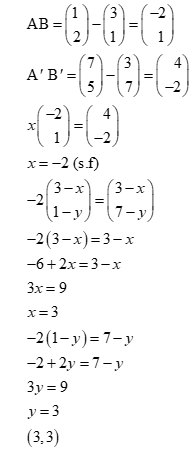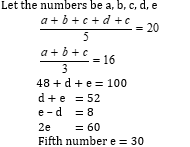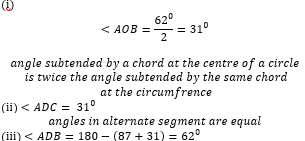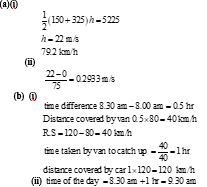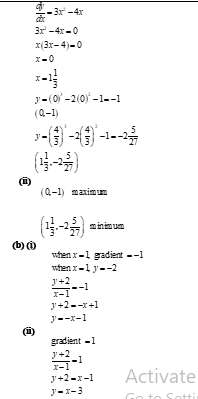Mathematics Paper 1 Questions and Answers - Nginda Girls Mock Examination 2023

Instructions to Candidates

• Answer ALL questions in section I and STRICTLY ANY FIVE questions from section II.
• Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
• Marks may be awarded for correct working even if the answer is wrong.
  printed as indicated and no question is missing.

QUESTIONS

SECTION I(50marks)
Answer all the questions in this section

1. Without using a calculator evaluate. (3marks)
   
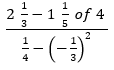
2. A piece of rectangular plot measuring 27m by 16m is to be divided into smaller rectangular units leaving no remainder. Calculate the highest number of smaller units whose dimensions are each greater than 1m that can be obtained from the plot. (3marks)
3. Given that x=1.3 ̇13 ̇, find the exact value of . (3 marks)
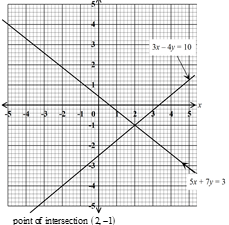
4. Using the grid provided below, solve the simultaneous equation (3 marks)
   
   3x-4y=10
   5x+7y=3
5. Write the following ratios in ascending order  2:3, 15:16, 7:6, 13:15 (3 marks)
6. Under an enlargement, the image of the points A(3,1) and B(1,2)are A'(3,7) and B'(7,5). Find the centre and scale factor of enlargement. (4 marks)
7. A Kenyan businessman intended to buy goods worth US dollar 20,000 from South Africa. Calculate the value of the goods to the nearest south Africa (S.A) Rand given that 1 US dollar = Ksh 101.9378 and 1 S.A Rand = Ksh 7.6326. (3marks)
8. Solve for x in the following equation. (3marks)
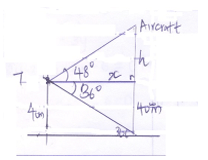
   4x (8x - 1) = (sin45°)/(cos45°)
9. From a viewing tower 40 metres above the ground, the angle of depression of an object on the ground is 36° and the angle of elevation of an aircraft vertically above the object is 48°. Calculate the height of the aircraft above the objet on the ground. (3marks)
10. Solve the equation 2x² + 3x= 5 by completing the square method. (3marks)
11. The mean of five numbers is 20. The mean of the first three numbers is 16. The fifth number is greater than the fourth by 8. Find the fifth number. (3marks)
12. Simplify: (3 marks)
    
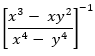
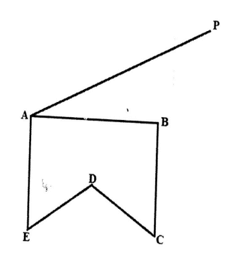
13. The figure below ABCDE is a cross-section of a solid ABCDEPDRST. The solid has a uniform cross-section. Given that AP is an edge of the solid, complete the sketch showing the hidden edges with a broken line. (3 marks)
    
14. In the circle below, O is the centre, angle DAB = 87° and acute angle A0D=62°. CD is a tangent to the circle at D.
    
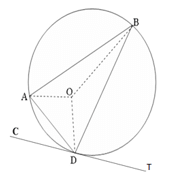
    Calculate the size of;
    1. Angle ABD. (2marks)
    2. Angle ADC (1mark)
    3. 0Angle ADB (1mark)
15. Given that log a = 0.30 and log b = 0.48 find the value of log b²/a. (3marks)
16. The area of a rhombus is 60cm². Given that one of its diagonal is 15cm long. Calculate the perimeter of the rhombus. (3marks)

SECTION II (50marks)
Answer 5 questions only in this section

17. Three business partners Abila, Bwire and Chirchir contributed Ksh120,000, Ksh 180,000 and Ksh 240,000 respectively to boost their business. They agreed to put 20% of the profit accrued back into the business and to use 35% of the profits for running the business. The remainder was to be shared among the business partners in the ratio of their contribution. At the end of the year, a gross profit of Ksh225,000 was realised.
    1. Calculate the amount.
       1. Put back into the business. (2marks)
       2. Used for official operations. (1mark)
    2. Calculate the amount of profit each partner got. (4marks)
    3. If the amount put back into the business was added to individual’s shares proportionately of their initial contributions, find the amount of Chirchir’s new shares. (3marks)
18. One day Mr. Makori bought some oranges worth Ksh 45, on another day of the same week his wife Mrs.Makori spent the same amount of Money but bought the oranges at a discount of 75 cents per orange
    1. If Mr.Makori bought an orange at Kshs x, write down and simplify an expression for the total number of oranges bought by the two in the week. (3marks)
    2. If Mrs.Makori bought 2 oranges more than her husband, find how much each spent on an orange. (5 marks)
    3. Find the number of oranges bought by the two. (2 marks)
19. Two lines L1:2y – 3x -6 = 0 and L2 = 3y + x – 20 = 0 intersect at a point A.
    1. Find the coordinates of A (3 marks)
    2. A third line L4 is perpendicular to L2 at point A. Find the equation of L3 in the form y = mx + c, where m and c are constants. (3 marks)
    3. Another line L4 is parallel to L1 and passes through (-2, 3). Find the x and y intercepts of L4 (4 marks)
20. The mases to the nearest kilogram of some student were recorded in table below
    

    Mass (kg)	41-50	51-55	56-65	66-70	71-85
    Frequency	8	12	16	10	6
    Height of rectangle					0.2

    
    
    1. Complete the table above to 1 decimal (2 marks)
    2. On the grid provided below, draw a histogram to represent the above information (3 marks)
       
    3. Use the histogram to
       1. State the class in which the median mark lies. (1 mark)
       2. Estimate the median mark (2 marks)
       3. The percentage number of students with masses of at least 74kg. (2marks)
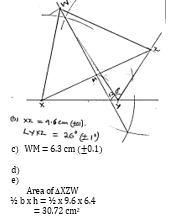
21. Use a ruler and compass only for all the constructions in this question.
    1. Construct a triangle XYZ in which XY= 6cm, YZ =5cm and angle XYZ= 120°. (2marks)
    2. Measure XZ and angle YXZ. (2 marks)
    3. Construct the perpendicular bisector of XZ and let it meet XZ at M. (1 mark)
    4. Locate a point W on the opposite of XZ as Y and that XW = ZW and YW =9cm and hence complete triangle XZW. (2 marks)
    5. Measure WM and hence calculate the area of triangle XZW. (3 marks)
22. The diagram below shows the speed time graph for a bus travelling between two stations, the bus starts from rest and accelerates uniformly for 75 seconds. It then travels at constant speed for 150 seconds and finally decelerates uniformly for 100 seconds
    .
    
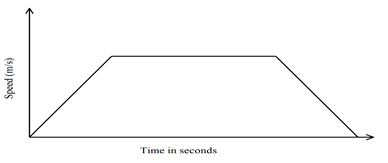
    1. Given that the distance between the two stations is . Calculate
       1. maximum speed in attained by the bus. (3 marks)
       2. the acceleration of the bus (2 marks)
    2. A van left Nairobi at 8.00 a.m and travelled towards Mombasa at an average speed of 80 km/h. At 8.30 am a car left Nairobi and travelled along the same road at an average speed of 120km/h.
       1. Calculate the distance covered by the car to catch up with the van. (4 marks)
       2. Find the time of the day when the car caught up with van. (1 mark)
23. While designing the water circulation system, planners of an estate used assumption that each housing unit in the estate will require at least 0.32m3 of water per day. To satisfy this need, they are to use a water pipe of radius 8cm to distribute the water. The water will be flowing in the pipe for only 14 hours a day at the rate of 24cm/s.
    1. Determine the amount of water to the nearest litres, supplied in one hour. (3marks)
    2. What is the maximum number of housing units that can be supported by the water circulation system? (Assume that a housing unit requires at most 0.32m3 of water per day). (2marks)
    3. Each housing unit will pay a flat rate of sh. 280 per month for the supply of water. If the number of housing units in the estate is to be maximum and all end up being occupied, calculate the amount of money that will be collected in a month. (2 marks)
    4. The maximum number of housing units were constructed and all got occupied. The estate ended up using on average 0.35m3 of water per housing unit per day. How much longer was the water pumped per day to satisfy the estate’s water demand? (3marks)
24. The equation of the curve is  y=x³-2x²-1
    1. Determine
       1. the stationary points (4marks)
       2. the nature of the stationary points in (a) (i) above (2 marks)
    2. Determine
       1. the equation of the tangent to the curve at (2marks)
       2. the equation of the normal to the curve at (2marks)

MARKING SCHEME

	Section I
1.	6⁄5*4=24⁄5 7⁄3-24⁄5=35-72/15=-37/15  1⁄4-1⁄9=9-4/36=5⁄36 -37⁄15*36⁄5=17 19⁄25	M1 M1 A1
		3
2.	27=3*3*3 16=2*2*2*2 Dimension of the smaller unit =3*2 no of smaller unit = 27*16/3*2 =72 units	M1 M1 A1
		3
3.	x=1.313313313 1000x= 1313.13313313 999x=1312 x=1312      999	M1 M1 A1
		3
4.
		3
5.
		3
6.		B1	For both value of x and y  For coordinate
		4
7.		M1 M1 A1	Expression Expression CAO
		03
8.		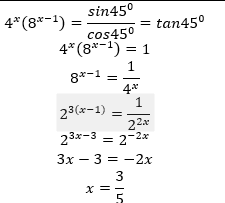M1 M1 A1	Comparing powers
		3
9.	Tan 36o = 40x           x =40/ Tan 36              = 55.06m  Tan 48 = h/55.06           h = 61.15m (61.15 + 40) = 101.15m	M1 M1 A1	ü  For value of x Height of aircraft from object
		3
10.	x2+3⁄2x + (3⁄4)2 =5⁄2 + (3⁄4)2 (x+3⁄4)2 = 49⁄16 x+3⁄4 =+- √49⁄16 x=-3⁄4 +- 7⁄4 x=2.5 or 1	M1 M1 A1
		3
11.		M1  M1 A1
		3
12.		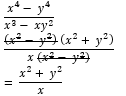M1 M1 A1
		03
13.		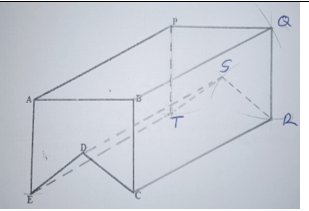B1 B1 B1	Broken edges Locating Q,R,S,T Complete diagram
		3
14.		B1 B1 B1 B1
		4
15.	=log b2⁄a = log b2 - log a 2(0.48) – 0.30 0.96 – 0.30 = 0.66	M1 M1 A1
		03
16.		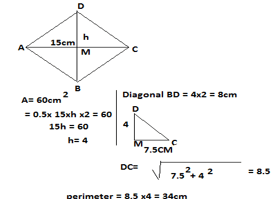M1 M1 A1	Height Base Perimeter
		3
	SECTIONII
17.	for    for    for    for    for    for    for    for    for    for		for for    for for   for    for    for    for
		10
18.	(a).45⁄x + 45/x-0.75      = 45(x-0.75) + 45x               x(x-0.75)      = 45x – 33.75 + 45x           x2 – 0.75x (b). 45 + 2 =   45__            x        x-0.75 45(x - 0.75) + 2x(x- 0.75) = 45x  45x - 33.75 +2 x 2 - 1.5x =  45x              2x2 - 1.5x - 33.75 = 0                    8x2 - 6x - 135 = 0         8x2 - 36x + 30x -135 = 0     4x(2x - 9) + 15(2x – 9) = 0                   4x = -15 or 2x = 9                    x = -3.75 or x = 4.5 Makori spent sh 4.50 per orange           Mrs Makori spent sh 3.75 per orange (c). N.of oranges =45/4.50+45/3.75 = 10 + 12 = 22 oranges	M1 M1 AI M1 MI MI M1 A1 M1 A1	-simplified equ. Equating to zero For factors For both
		10
19.	a) 2y - 3x = 6 3y + x =20 x = 20 – 3y 2y – 3(20 – 3y)=6 2y – 3(20 – 3y) – 6 = 0 2y – 60 + 9y – 6 = 0   11y = 66                y = 6       x = 20 - 3 (6)                              = 20 – 18                  x = 2 Co-ordinates of A (2,6) (b). L2M2 3y = 20 - x             y =   - x         M1 =         M3 = 3          . = 3 y = 3x – 6 + 6 y = 3x (c). 2y = 6+3x         y =3 + x      M1 =      M4 =   = 2y = 3x+6+6 .y = x + y = x + .x-intecept (y = 0) 0 =x + 6 -6 = x x= -4 x-intercept = -4 if intercept (x=0) y = (0) + y = 6 y-intercept  = 6	M1 AI B1 B1 M1 A1 B1 M1 B1 B1	(both)
		10
20.	Mass (kg) 41-50 51-55 56-65 66-70 71-85 Frequency 8 12 16 10 6 Height of rectangle 0.4 1.2 0.8 1.0 0.2   c) (i) 56-65      (ii)55.5+6/2*0.8          =55.5+3.75=59.25       d)5⁄52*100=9.615%	B2 B1 B1 B2 B1 B1 M1 A1 M1A1	For all For any 3 Scale For all bars For 3 bars
21.	c)   WM = 6.3 cm (0.1) d)      e)        Area of ΔXZW ½ b x h = ½ x 9.6 x 6.4             = 30.72 cm2	B1 B1 B1 B1 B1 B1 B1 B1 M1 A1	For 120o construction Complete construction of DXYZ Length Angle YXZ Perp bisec of XZ to M Correct location of W Complete DXZW Length WM
22.
		10
23.		M1 M1 A1 M1 A1 M1 A1 M1 M1 A1	CAS
		10
24.