INSTRUCTIONS
- The paper contains two sections. Section I and Section II.
- Answer ALL the questions in section I and any five questions in section II.
- Show all steps in your calculations below each question.
- Marks may be given for correct working even if the answer is wrong.

QUESTIONS
SECTION I: 50 MARKS
ANSWER ALL QUESTIONS IN THIS SECTION
- Solve for x in the equation
2Sin2x - 1 = Cos2x + Sinx for 0≤x≤360 (3 Marks) -
- Expand (1+3⁄x)5 upto the fifth term (2 Marks)
- Hence use your expansion to evaluate the value of (2.5)5 to 3 d.p. (2 Marks)
- Make p the subject of the formula (3 Marks)
- A object A of area 10cm2 is mapped onto its image B of area 60cm2 by a transformation whose matrix is given by Find the possible value of (3 Marks)
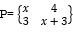
- A variable Z varies directly as the square of X and inversely as the square root of Y. Find the percentage change in Z if X increased by 20% and Y decreased by 19% (3 Marks)
- A circle whose equation is (x – 1)2 + (y – k)2 = 10 passes through point (2,5). Find the coordinates of the two possible centres of the circle.(3marks)
- Juma deposited Sh. 45 000 in a bank which paid interest at 12% p.a compounded monthly. Calculate the amount of interest after 3 years (3 Marks)
-
- Find the inverse of the matrix
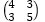 (1 Mark)
(1 Mark) - Hence solve the simultaneous equation below using matrix method (3 Marks)
4x + 3y = 6
5y + 3x – 5 = 0
- Find the inverse of the matrix
- Given that P=4+√2 and Q=2+√2 and that P/Q=a+b√c , where a, b and c are constants, find the values of a, b and c. (3 marks)
- Find the value of x that satisfies the equation: log3(x+24)-2=log3 (9-2x) (3 marks)
- Under a shear with x-axis invariant the point (3,2) is mapped onto (-2,2). Find the image of point (4,4) under the same transformation.(3marks)
- The data below shows the marks obtained by ten students in a test. 71, 55, 69, 45, 65, 57, 71, 82, 55, 50
Find the quartile deviations. (3 marks) - A bag contains 4 green, 9 purple and 18 blue balls. The balls are identical except for the colour. Two balls are picked at random, one at a time without replacement, find the probability that, a blue ball and a green ball are picked. (3 marks)
- Find the equation of the tangent to the curve y = x2 + 2x + 3 at the point where the gradient is equal to 4. (3 marks)
- The radius of a spherical ball is 2.5cm correct to one decimal place. Calculate the percentage error in calculating the surface area of the ball (3 marks)
-
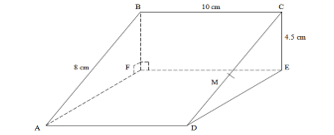
The above diagram represents a wooden prism. ABCD is a rectangle. Points E and F are directly below C and B respectively. M is the mid-point of CD. AB = 8 cm, BC = 10 cm and CE = 4.5 cm. Calculate the Angle CAE makes with the plane ADEF (3marks)
SECTION II: 50 MARKS
ANSWER ANY 5 QUESTIONS IN THIS SECTION
- In the figure below, OA = ãandOC = c∼. CB = 2⁄3 OA and Bdivides CD in the ratio 3: 1
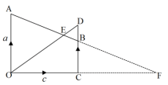
- Express the following vectors in terms of a and c only:
- AB (1 mark)
- OD (2 marks)
- Given that OE=hOD and AE=kAB where h and k are scalars express OE in two different ways hence find the scalars h and k. (5 marks)
- If OC produced meets AB produced at F, find OF . (3 marks)
- Express the following vectors in terms of a and c only:
-
- The 5th term of an AP is 82 and the 12th term is 103. find:
- the first term and common difference. (3marks)
- the sum of the 21 terms. (2 marks)
- A stair case was built such that each subsequent stair has a uniform difference in height. The height of the 6th stair from the horizontal floor was 85 cm and the height of the 10th stair was 145. Calculate the height of the 1st stair and the uniform difference in height of the stairs. (3 marks)
- During the construction of the staircase, each step was supported by a vertical piece of timber. If the staircase has 11 stairs, calculate the total length of timber used. (2 marks)
- The 5th term of an AP is 82 and the 12th term is 103. find:
-
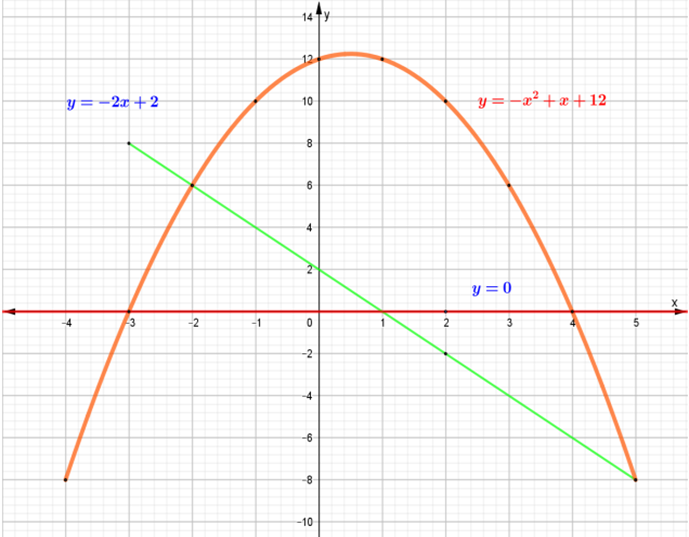
- Complete the table below given that y = -x2 + x + 12 for -4 ≤ x ≤ 5 (2 marks)
X
-4
-3
-2
-1
0
1
2
3
4
5
Y
8
12
12
- On the grid provided below, draw the graph of y = 〖-x〗^2 + x + 12 for -4 ≤ x ≤ 5
Scale: 1 cm represents 1 unit on the x – axis and 1 cm represents 2 units on the y – axis. (4 marks)
- Using your graph, to Solve the equation x2-3 x- 10=0 (2 marks)
- State the range of values of x for which -x2 + x + 12≥ 0 (1 mark)
- Estimate the coordinates of the turning point of the curve y =-x2 + x + 12 (1 mark)
- Complete the table below given that y = -x2 + x + 12 for -4 ≤ x ≤ 5 (2 marks)
- An aircraft leaves town P(30°S,17° E)and moves directly to town Q(60°N,17°E) . It then moved at an average speed of 300 knots for 8 hours westwards to town R. Determine;
- The distance PQ in nautical miles. (3 marks)
- The position of town R. (3 marks)
- The local time at R if the local time at Q is 3:15 p.m (2 marks)
- The total distance moved from P to R in km. Take 1nm=1.853 km (2 marks)
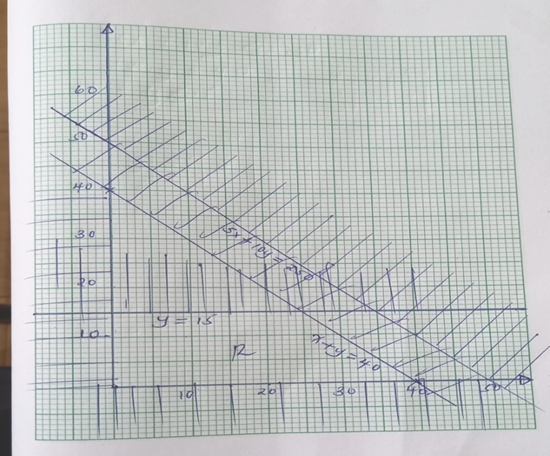
- Using a ruler and compasses only.
- Construct a parallelogram ABCD such that AB = 10cm, BC = 7cm and angle ABC = 105º. (3 marks)
- Construct the loci of P and Q within the parallelogram such that 6cm. AP≤4cm and BQ≤6cm (3 marks)
- Calculate the area within the parallelogram but outside regions bounded by the loci of P and Q. (4 marks)
- Below is the histogram representing marks obtained in Mathematics test
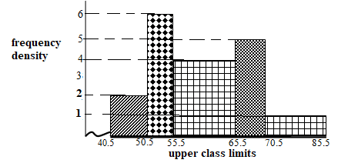
- Develop a frequency distribution table for the data (3 Marks)
- Using an assumed mean of 60.5 find the mean. (3 marks)
- Calculate Standard deviation. (4marks)
-
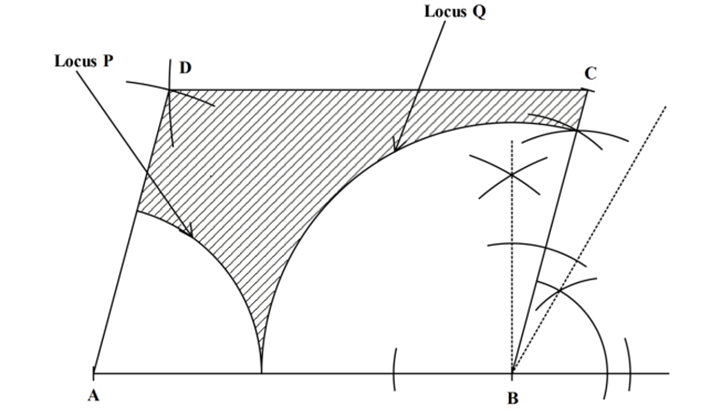
- Use the mid ordinate rule with 5 strips to estimate the area bounded by the curve y=x2-3x 4,x=-2,x=3 and x-axis (3 marks)
- Calculate the exact area above (5 marks)
- Find the percentage error involve in using the mid-ordinate role. (2 marks)
- Eldoret Airport is planning to build a fire fighting plant on a space of 250m2. Two types of machines are to be installed, machine x which occupies a space of 5m2 and machine Y which occupies 10m2. The airport can have a maximum of 40 machines at a time. At most 15 machines of type Y are used at any given time.
- Write down three inequalities other than x>0, and y>0. (3marks)
- On the grid below, show the region satisfying the given conditions. (4marks)
- The profit from a type x machine is Ksh 1000 and that of type y is Ksh 4000. Use the graph to obtain the number of machines of each type that should be installed to obtain maximum profit. Calculate the maximum profit. (3marks)

MARKING SCHEME
SECTION I
|
|
WORKING |
MARKS |
GUIDELINES |
|
1. |
2sin2x-1 = 1-sin2x + sinx 3sin2x-sinx-2 = 0 (3sinx + 2 )(sinx-1)=0 either sinx =0.6667 or sinx =1 90.221.81,318.19 |
M1 M1 M1 A1 |
|
|
|
4 |
||
|
2. |
|
M1 A1 M1 A1 |
|
|
|
3 |
||
|
3. |
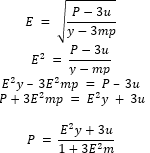 |
M1 M1 A1 |
Squaring Collecting terms in P Subject obtained |
|
|
3 |
||
|
4. |
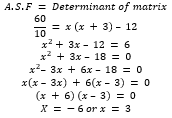 |
M1 M1 A1 |
Equation Factorization |
|
|
3 |
||
|
5. |
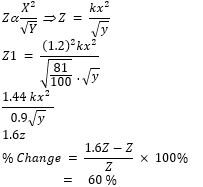 |
M1 M1 A1 |
(squaring on both sides) |
|
|
3 |
||
|
6. |
(2-1)2 + (5-k)2 =10 1+25*10k+k2=10 (k-2)(k-8)=0 k=2or8 centre (1,2) and (1,8) |
M1 M1 A1 |
|
|
7. |
Amount after 3 years (36 monthly periods) =45000*(1+1/100)36 =ksh. 64384.60-45000) intrest=ksh (64 384.60 - 45000) =ksh.19.384.5953 |
M1 M1 A1 |
|
|
|
3 |
||
|
8. |
|
M1 M1 A1 |
|
|
|
3 |
||
|
9. |
|
M1
A1 B1 |
|
|
|
3 |
||
|
10. |
log3(x+24) -log39 = log3(9-2x) log3(x+24/9) = log3(9-2x) (x+24/9)=(9-2x) x+24=81-18x x=3 |
M1 M1 A1 |
|
|
|
3 |
||
|
11. |
|
M1 M1 A1 |
|
|
|
3 |
||
|
12. |
45,50,55,55,57,65,69,71,71,85 |
M1 M1 A1 |
|
|
|
3 |
||
|
13. |
P(BG or GB) 4/31 * 18/30 + 18/31 * 4/30 36/465 + 36/465 =72/465 |
M1M1 A1 |
|
|
|
|
3 |
|
|
14. |
y = x2 + 2x + 3 |
M1 A1 B1 |
|
|
|
3 |
||
|
15. |
|
M1 M1 A1 |
|
|
|
3 |
||
|
16. |
DE = 82 − 4.52 = 6.61cm |
M1 M1 A1 |
|
|
|
3 |
SECTION II
|
|
WORKING |
MKS |
GUIDELINES |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
17. |
 |
B1 B1 B1 M1 M1 M1 M1 A1 M1
A1
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
10 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
18. |
|
B1 M1 A1 M1 A1 B1 M1 A1 M1 A1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
10 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
19. |
 |
B2 S1 P2 C1 L1 B1 B1 B1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
10 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
20. |
a) distance PQ= 60*90 =5400nm |
B1 m1 A1 M1 M1 A1 M1 A`1 M1 A1 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
10 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
21. |
Area of parallelogram = 10*7 sin 75 =67.61cm2 |
B1 B1 B1 B1 B1 B1 B1 M1 M1 M1 A1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
10 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
22. |
a) mean = -75/130+60.5 = 59.92 |
B1 B2 B1 B1 B1 M1 A1 M1 M1 A1 |
Class Frequency d |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
10 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
23. |
|
B1 M1 A1 M1 M1 M1 A1 M1 A1 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
10 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
24. |
a) 5x + 10y 250 or x+2y50 ksh 85,000 |
B1 B1 B1 B1 B1 M1 A1 B1 B1 B1 B1 |
Objective function x and y substitution |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
10 |
Download Mathematics Paper 2 Questions and Answers - Nginda Girls Mock Examination 2023.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

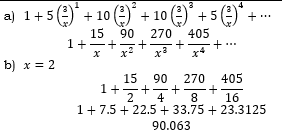
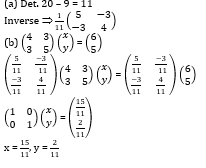
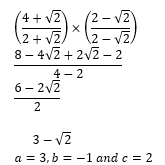
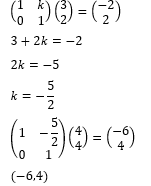

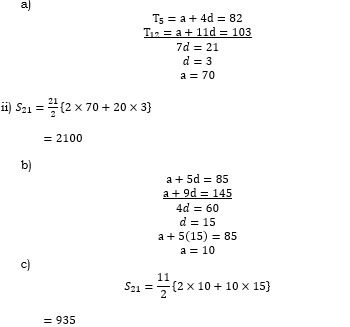
 c)
c)