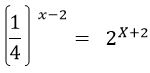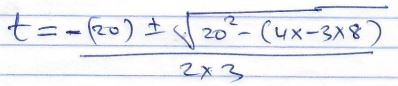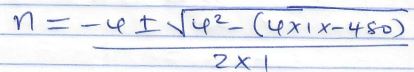Mathematics Paper 1 Questions and Answers - Samia Joint Mock Examination 2023

Instructions to candidates.

• This paper consists of two sections: Section I and Section II.
• Answer all the questions in Section I and only five questions from Section II
• Show all the steps in your calculations, giving your answer at each stage in the spaces provided below each question
• Marks may be given for correct working even if the answer is wrong.
• Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.

SECTION 1 (50 MARKS)

Answer all questions in the spaces provided.

1. A sum of money is divided between three men x, y and z in the ratio 5:3:1. If y has Shs. 700/= more than z, calculate how much x has.
   (3 marks)
2. Simplify the expression  12x² + ax - 6ax²           (3 marks)
                                                9x² - 4a²              
3. Find the integral values of x of which  (3 marks)
   5 ≤ 3x + 2
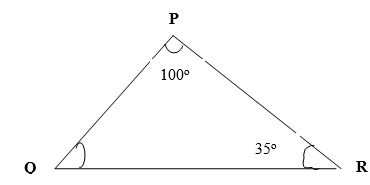
   3 x − 14 ≤ − 2
4. The figure below shows triangle PQR in which PQ = 7cm, angle QPR = 100° and angle PRQ = 35°. Calculate to 2 decimal places the length of PR hence the area of triangle PQR.
                                                          
5. Evaluate without using a calculator  3 marks)
               23.4 − 2(5.2 + 5.3)
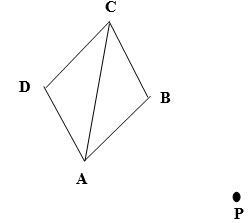
                      3.2 x 1.2 
6. The figure below represents a kite ABCD. Use a pair of compasses and ruler only to rotate it through -60° about point P.  (2 marks)
                                                                     
7. Find the inverse of the matrix (¹/₃ ¹/₁) hence determine the point of intersection of the lines. (4 marks)
         y + x = 7
         3x + y = 15
8. A trader had a bag of rice, when he packed the rice in 6kg packets, he had 1 kg left over, when he packed the rice in 8kg packets, again he had 1kg left over. When he packed the rice in 9kg packets, he had 1kg left over. What is the smallest amount of rice that he must have had.
   (3 marks)
9. A Histogram is drawn from the set of data given below. Complete the missing bars.  (3 marks) 
   

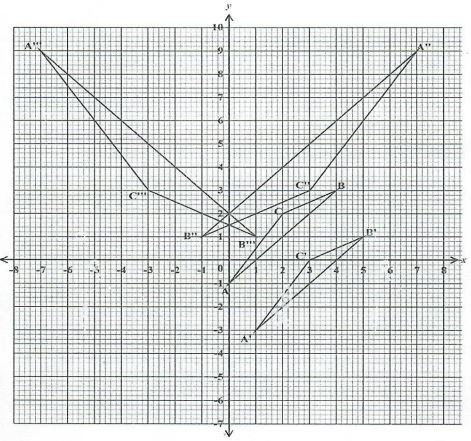
   Marks	6-10	11-20	21-35	36-55	56-65
   Frequency	8	14	18	24	10

10. Kinyua marked an article at Kshs. 1200/- and sold it to a customer at a discount of 15%. Find the percentage profit he made if he had bought the article at Kshs. 900/=.                (3 marks)
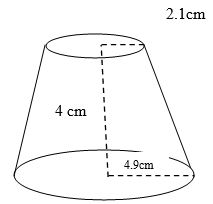
11. The diagram below represents a solid of a conical frustrum. (Use π ²²/₇) (4 marks)
                                                                             
    Calculate the volume of the solid
12. Given that a = (−28), b = −64) and c = −4 2 and given that = 4a − 8b + 6c, find /P/  (3 marks)
13. Evaluate using tables of reciprocals  (3 marks)
         5      +    1     
       807      0.0591
14. Solve for x in the following equation  (3 marks)
           
15. Each interior angle of a regular polygon is four times greater than the exterior angle. How many sides does this polygon have?  (3 marks)
16. A boat is at point P, a distance of 100km from the bottom of a hill. The angle of elevation of the top of the hill is 30° from P. The boat sails straight towards the hill to a point Q from where the angle of elevation to the top of the hill is now 60°. Calculate the distance PQ   (3 marks)

SECTION II (50 MARKS)

Answer only five question from this section in the spaces provided.

17. Given that a line L₁ passes through the points A(−1, 5) and B (3, −1), find
    1. The equation of line L1 in the form y = mx + c     (2 marks)
    2. The equation of a line L₂, which is a perpendicular bisector of L₁. Leave your answer in the form
       ax + by = c where a, b, c are integers  (3 marks)
    3. Given that another line L₃ is parallel to L₂ and passes through point (−3, −5) and intersects lines L₁ at point P. Find the equation of L₃ in the form ax + by +c = 0  (2 marks)
    4. The coordinates of the point of intersection of lines L₁ and L₃   (3 marks)
18. Four towns P, R, T and S are such that R is 70km directly to the north of P and T is on a bearing of 280° from P at a distance of 75km. S is on a bearing of 320° from T and a distance of 45km.
    1. Using a scale of 1cm to represent 10km, make an accurate scale drawing to show the relative position of the towns. (4 marks)
    2. Using your diagram above, find the distance in km of
       1. R from T  (3 marks)
       2. S from R
    3. From your diagram, what is the compasses bearing of (3 marks)
       1. R from T
       2. P from S
19. Nyaugenya bus leaves Port Victoria for Eldoret at 7:00 a.m. at an average speed of 80km/h. Climax bus leaves Eldoret towards Port Victoria at 7:30 a.m on the same day using the same route at an average speed of 60km/h. The distance from Eldoret to Port Victoria is 450km. After travelling for one hour and a half, climax bus developed a mechanical problem which took 45 minutes to repair before continuing at its speed in the same direction.
    1. Determine the time when the two buses met. (4 marks)
    2. Calculate the distance from Eldoret at the time of the two buses meeting.  (3 marks)
    3. For how long did the Nyaugenya bus stay in Eldoret before Climax bus arrived at Port Victoria.  (3 marks)
20.  
    1. On the grid provided draw triangle ABC with vertices A(0, -1), B(4, 3) and C(2, 2)   (1 mark)
         
    2. Draw triangle A¹B¹C¹, the image of ABC under a translation defined by the translation vector T = (¹ ₋₂)  (3 marks)
       Write down the coordinates A¹B¹C¹.
    3. A¹¹B¹¹C¹¹ is the image of ABC under an enlargment, scale factor −2, centre (3,1). On the same grid draw A¹¹B¹¹C¹¹ and write down its coordinates.
    4. Draw A¹¹B¹¹C¹¹, the image of A¹¹B¹¹C¹¹, 1 under reflection on the line x = 0
21. The motion of a particle P moving along a straight line is described by the equation S = (8+10t)t – t³
    Calculate;
    1. The distance when t = 3 sec.  (2 marks)
    2. The maximum velocity of the motion. (4 marks)
    3. The acceleration of motion after 4 seconds.  (2 marks)
    4. The time at which the velocity is zero.  (2 marks)
22. 1. Use the trapezium rule with 8 ordinates to approximate the area under the curve   (5 marks)
       y = x² + x + 3 and the x-axis between lines x = −3 and x = 4 
    2. Use the mid-ordinate rule with 5 strips to calculate the area under the curve y = 3x² + 8 and bounded by lines y = 0, x = 1 and x = 6.
       (5 marks)
23. Three people; A, B and C work together to make a certain number of tins. It person C was to work alone he will take 4⁴/₉ hours to complete the job. If all working together they will take 1 hour 40 min. to complete the job. They all started working together however person B left after the first 40 minutes, while person C left 20 minutes later. Person A took a further 1hr 46mins. Calculate how long it would take if all the tins were made by;
    1. Person A alone  (6 marks)
    2. Person B alone (2 marks)
    3. Person A and C alone  (2 marks)
24. In Busia County, a tailor bought a number of suits at a cost of Shs. 57,600/= from a wholesaler. Had he bought the same number of suits from a supermarket, it would have cost him Shs. 480/= less per unit. This would have enabled him to buy four extra suits for the same amount of money.
    1. By letting the number of suits that the tailor bought to be n, write an expression in n for cost of a suit from;
       1. The wholesaler (1 mark)
       2. The supermarket (1 mark)
    2. Find the number of suits that the trailer bought  (4 marks)
    3. The tailor later sold each suit for Shs. 720/= more than he paid for it. Determine the percentage profit he made.    (4 marks)

MARKING SCHEME 

No.	Working	Marks Allocation
1.	3 − 1 = 2   700 x 5        2  sh. 1750	B1 - difference in ratio    M1    A1
		03
2.	12x2 + 9ax − 8ax − 6a2   3x(4x + 3a) −2a(4x + 3α)   (4x + 39) (3x − 2a)   (3x − 29) (3x + 2a)   (4x + 39)(3x − 29)     (3x − 29) (30 + 24)         4x + 39         3x + 29	B1    B1    A1
		03
3.	3 ≤ x   1 ≤ x       or    x ≥ 1    3x ≤ 12     x ≤ 4       or    4 ≥ x    x = 1, 2, 3, 4	B1    B2    A1
		03
4.	7       =  QR                Sin 35    sin 100             QR = 12.02 cm              ½ x 7 x 12.02 Sin 45         =   29.75cm2	M1    A1  ( C.A.O)    M1    A1
		04
5.	2.4      3.84     24 x 10        384       =  0.625	M1 - for simplifying    M1 - for cancellation   A1  ( C.A.O) DO NOT AWARD IF FRACTION
		03
6.		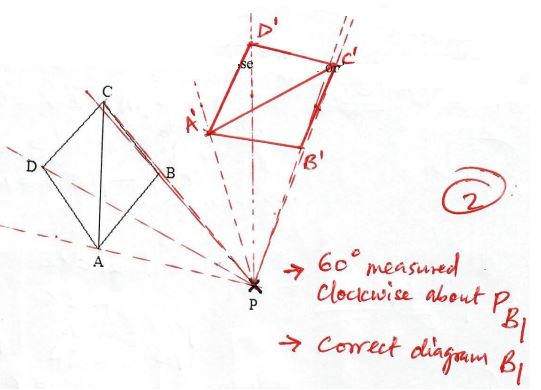B1 - for 60° measurement clockwise about                      0     B1 - for correct diagram
		02
7.	(1 x 1) − (3 x 1)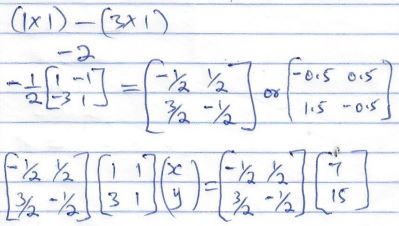	M1 - For determinant    A1 - C.A.O    M1 - For premultipying by inverse            otherwise award 0    A1
		04
8.	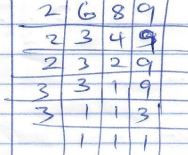LCM = 23 x 32            = 72   Amount of rice = 72 + 1                           = 73 kg	M1 - For finding lcm    M1 - for adding 1    A1
		03
9.		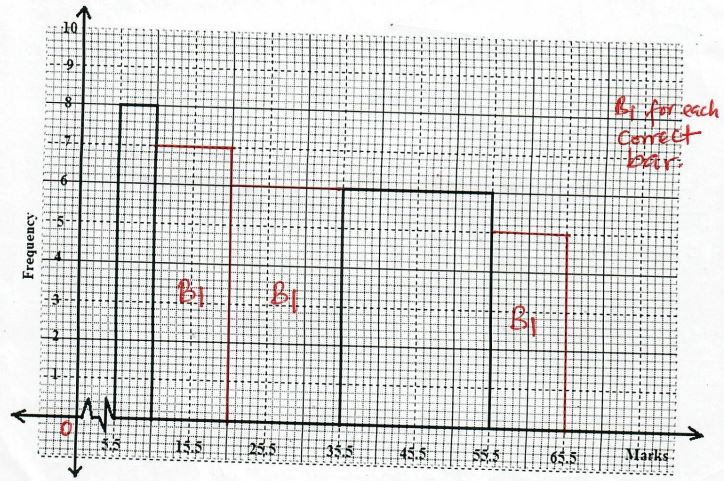B1 - Each correct bar B1    Three correct bars drawn
		03
10	S.P = 85 x 1200           100         = 1020   profit = 1020 − 900            = 120   % profit = 120 x 100                     900                = 13 1/3 or 13.3 or 13.33%	M1 - for selling price                        calculations     M1 - for % profit calculation     A1
		03
11.	h    =    2.1    h + 4       4.9    h = 3    Vol = 1/3 x 22/7 ( 4.92 x 7 − 2.12 X 3)          = 162.2133 cm3	M1 - for finding height of the                   original cone    B1 - for height    M1 - for finding volume    A1
		04
12.	P   = 4 (−2 8) −8 (–6 4) + 6(–4 2)         = (16 12)   /P/ = √162 + 122        = 20 units	M1 - for substitution   M1 - for calculation of magnitude    A1
		03
13.	(5 X 0.1293 X 10−2)     0.006195    0.1692 X 102      16.92    0.006195 + 16.92 = 16.926195	B1 - for finding reciprical using                tables   B1 -  for finding reciprical using                tables    A1 - no mark for using calculators            C.A.O
		03
14.	(2−2)(x − 2)  =  2(x + 2)    −2x + 4 = x + 2      x = 2/3	M1 - for expressing to similar                   base.   M1 - for interpretation of equation    A1
		03
15.	x + 4x = 180          x = 36   n = 360          36      = 10	M1   M1   A1
		03
16.	tan 30 = h/100   100tan30 = h    tan 60 =  100tan30                     100 − x     x = 662/3km or 66.6km	M1 - for finding height   M1 - for substituting height    A1 - Accept 4.sf.
		03
17.	M1 = −1 − 5           3− (−1)       = −3/2    y − 5  = − 3   x −(−)       2   y = −3/2x + 7/2 M2 = 2/3 Midpoint = (1,2) y − 2 = 2 x − 1    3 2x − 3y = − 4 or −2x + 3y = 4 M3 = 2/3 y − (−5) =  2 x − (−3)     3 2x − 3y − 9 = 0 or −2x + 3y + 9 = 0 2x − 3(−3x + 7) − 9 = 0              2      2 x = 3 y = −3 x 3 + 7        2           2    = −1 P(3, −1)	M1 - correct substitution   A1        B1 - for both M2 & midpoint                   correct   M1 - correct substitution    A1      M1 - correct substitution  A1        M1 - correct substitution       M1 - correct substitution   A1
		10
18.	9.4 x 10     94km ± 1km   10.5 x 10    105km ± 1km    N52°E ± 1° S65°E ± 1°	M1    A1        M1    A1    B1    B1
19.	Distance by Nyangenya = 80 x (½ + 1½ + ¾)                                          = 220km  Distance by Climax = 60 x 1½                                  = 90km RD = 450 − (220 + 90)       = 140km RS = 80 + 60       = 140km/h T = 140       140     = 1hr Time of meeting = 7:30                               3:15                            = 10.45 a.m Time by Climax bus = 1.5 + 1                                  = 2.5h Distance = 60 x 2.5                = 150km Time taken by Nyangenya =  150                                                 80                                            =  17/8 hr Time taken by Climax =  300                                          60                                     = 5h Time difference = 5h − 17/8	B1 - for distcance by both buses    B1 - for both RD & RS    M1     A1    M1    M1    A1(accept relevant alternative)    M1    M1
		10
20.	A1 (1, −3) , B1 (5, 1), C1(3, 0) A11 (7, 9), B11 (−1, 1), C11 (3, 3)	B1 - for correct Δ ABC   B2 - for correct Δ A1B1C1   B3 - for correct Δ A11B11C11      B2 - for correct Δ A111B111C111                 B1 - for correct co-ordinates   B1 - for correct co-ordinates
		10
21.	s = (8 + 10(3))3 − 33    = 87 m v = 8 + 20t − 3t2 a = 20 − 6t 6t = 20 t = 10/3 v = 8 + 20 (10/3) −3(10/3)2   = 411/3 or 41.3 a = 20 − 6(4)   = 4m/s2 8 + 20t − 3t2 = 0 = 7.045 sec 0r − 0.375 ∴ t = 7.045 sec	M1 - correct substitution   A1      B1 - for correct a   M1 - for correct substitution   M1 - for correct substitution   A1   M1 - correct substitution   A1   M1    A1
		10
22.	x  − 3  − 2  − 1  0  1   2   3   4  y = x2 + x +3   9 5  3  3  5  9  15  23 A = ½ x 1{(9 + 23) + 2(5 + 3 + 3 +5 + 9 + 15)}    = 56 sp. units    x   1.5  2.5   35   4.5   5.5   y = 3x2 + 8  14.75  2 6.75   44.75   68.75   98..75 A = 1(14.75 + 26.75 + 44.75 + 68.75 + 98.75)    = 253.75 sq units	B3 - for all correct   B2 - for any 5 correct   B1 - for any 3 correct   M1    A1      B1 - for all correct    B2 - for all correct    B1 - for any 3 correct     M1      A1
		10
23	A + B + C ⇒ 1h 40 min = 5/3h   ∴ Work done in 1h = 3/5 ⇒ work done in 40min       40/60 x 3/5 = 2/5 Let work completion by A and B be a and b respectively. C  takes 40/9 h ∴ When B leaves, work done by A and C = 20/60 (1/9 + 9/40)                                                                  = 1/3a + 3/40 When C leaves, work done by A = 1/a (53/30a                                                     = 53/30a ∴ Completing the job     2/5 + 1/3a + 3/40 + 53/30a = 1                                     a = 4h 1/4 + 1/b + 9/40 = 3/5              1/b = 1/8                b = 8h 1/4 + 9/10 = 19/40	B1 - for work done in 40                minutes    M1 - for work done by             A & C    B1         M1 - for work done by all     A1       M1 - for work done by the              3      A1      M1 - for work done by A
24	57600      n 57600  n + 4   57600 − 57600 = 480     n          n + 4 n2 + 4n − 380 = 0 n = − 24 or 20 ∴ No. of suits bought = 20 720 x 20  1400 14400 x 100 57600 = 25%	B1    B1   M1    B1 - for correct quadratic                equation   M1 - accept any other                    method    A1   M1   B1    M1   A1 - acccept alternative