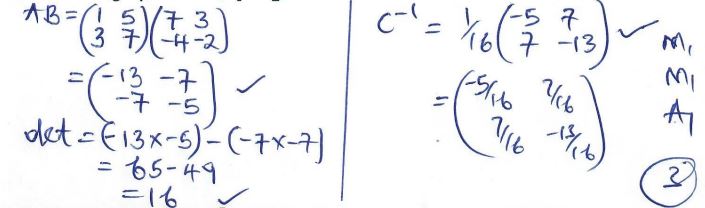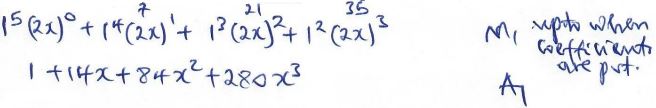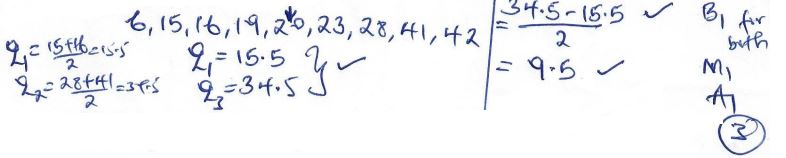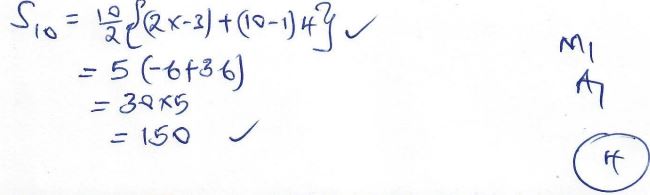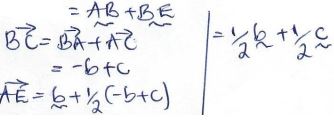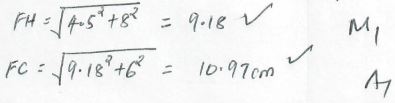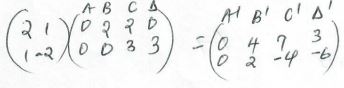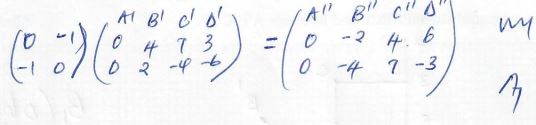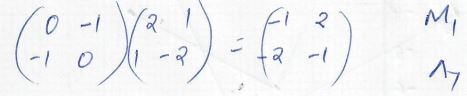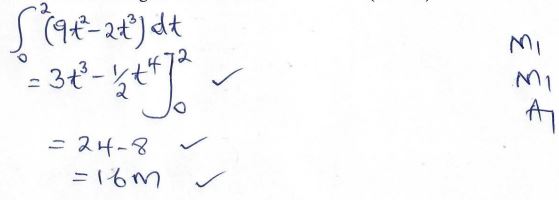Mathematics Paper 2 Questions and Answers - Samia Joint Mock Examination 2023

INSTRUCTIONS TO CANDIDATES

• The paper consists of two sections: Section I and Section II.
• Answer ALL questions from section I and ONLY FIVE from section II
• All answers and workings must be written on the question paper in the spaces provided below each question.
• Show all the steps in your calculation, giving your answer at each stage in the spaces below each question.
• Non – Programmable silent electronic calculators and KNEC mathematical tables may be used, except where stated otherwise.

(SECTION I : 50 MARKS)

1. Use logarithms to evaluate. (4marks)
                                
2. Make x the subject of the formula. (3 marks)
                              
3. Given that   8   = a + b√3 and that a and b are rational numbers, find the values of a and b. (3 marks)
                    4 − 2√3
4. Given that A = (1 5 3 7 ) and B = ( 7 3 − 4 ) and that C = AB, find C^-1 (3 marks)
5.  
   1. Expand and simplify (1 + 2x)⁷ up to the term in x³ (2 marks)
   2. Use the expansion in (a) above to estimate the value of (1.02)⁷ correct to four decimal places. (2 marks)
6. Solve for x in: log (7x + 2) – log (x – 1) = 0 (3 marks)
7. Find the quartile deviation for the following set of data (3 marks)
   16, 42, 41, 6, 20, 28, 19, 23, 15
8. The radius and height of a cylindrical tank rounded to 1cm are 105cm and 300cm respectively. Calculate the percentage error in its volume. (to 4 s.f) (3 marks)
9. Give that 25x² − 20x + k is aperfect square. Find the value of K.   (2 marks)
10. Solve for x in the equation; (3 marks)
    2Sin²x − 1 = Cos²x + Sin x, for 0° x ≤ 360°  
11. P and Q are two points on the earth’s surface. Their positions are P (60°S, 30°E) and Q (60°S, 90° W).Find the distance between P and Q along the parallel of latitude in km (Take radius of earth = 6370 km and π = ²²/₇) [to 1 decimal place.) (3 marks)
12.  
    1. The sum of the fifth and sixth term of an AP is 30. If the third is 5, find the first term. (2 marks)
    2. The sum of the first 10 terms of the AP (2 marks)
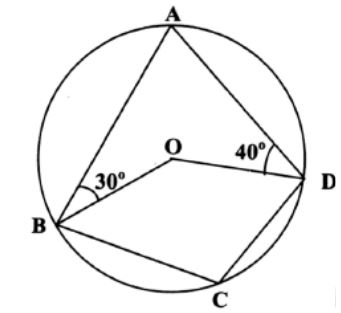
13. In the figure below, ABCD is a cyclic quadrilateral. Point O is the centre of the circle. Angle ABO = 30° and angle ADO=40°
                                                                        
    Calculate the size of angle BCD. (2 marks)
14. Obtain the Centre and radius of the circle represented by the equation.   (3 marks)
    x² + y² − 10y + 16 = 0
15. John bought 3 brands of tea A, B and C.  The cost price of the three brands was sh.25, sh.30 and sh.45 per kilogram respectively.  He mixed the three brands in the ratio 5:2:1 respectively.  After selling the mixture he made a profit of 20%.  How much profit did he make per kilogram of the mixture?                         (4mks)
16. Draw a line DF= 4. 6cm.Construct the locus of point K above DF such that angle DKF = 70°. (3 marks)

SECTION II (50 MARKS)

(Answer ONLY FIVE questions in the spaces provided)

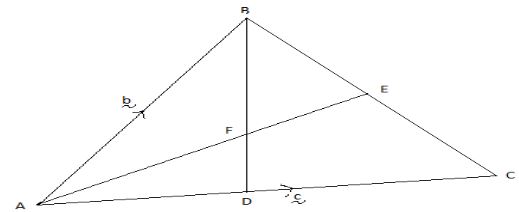
17. In the figure below, E is the midpoint of BC. AD : DC = 3:2 and F is the meeting point of BD and AE.
                                      
    1. Express the following vectors in terms of b and c
       
       1.     (2 marks)
       2.       (2 marks)
    2. If BF = tBD and AF = nAE, find the value of t and n (5 marks)
    3. State the ratio in which F divides BD and AE (1 mark)
18. The probability that a boy goes to school by bus is ¹/₃ and by matatu is ¹/₂ . If he uses a bus the probability that he is late to school is ¹/₅ and if he uses a matatu the probability of being late is ³/_10. If he uses other means of transport, the probability of being late is ¹/₂₀.
    1. Represent this information on a tree diagram. (2 marks)
    2. What is the probability that;
       1. He will be late to school (2 marks)
       2. He will not be late to school (2 marks)
       3. He will be late to school if he does not use a matatu. (2 marks)
       4. He neither uses a bus nor matatu but arrives to school early. (2 marks)
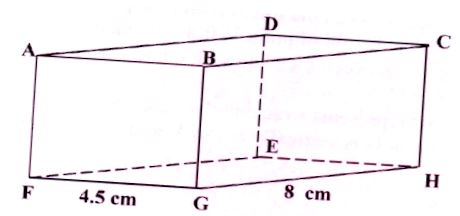
19. The diagram below represents a cuboid ABCDEFGH in which FG= 4.5 cm, GH = 8cm and HC = 6 cm
                                                              
    Calculate:
    1. The length of FC (2 mks)
    2.  
       1. the size of the angle between the line FC and the plane FGHE (2 mks)
       2. The size of the angle between the lines AB and FH (2 mks)
       3. The size of the angle between the lines AC and GE (2mks)
    3. The size of the angle between the planes ABHE and the plane FGHE (2 mks)
20. The table below shows the income tax rates
    

    Income per  annum in K£	Rate in Sh per K£
    1-1980	2
    1981-3960	3
    3961-5940	5
    5941-7920	7
    7921-9920	9
    Over 9920	10

    Juma is a salaried employee with a basic salary of Ksh. 15,710 per month and house allowance of sh1,350 monthly. He is also entitled to a monthly tax relief of Ksh1320.
    Calculate:
    1. Juma’s annual salary in K£. (2 marks)
    2. The monthly tax paid by Juma in Ksh. (6 marks)
    3. Find his net pay per month in Ksh. (2 marks)
21.  A transformation represented by the matrix  to map onto A 0,0) B(2, 0) C(2, 3) and D(0, 3) onto A¹B¹C¹D¹ respectively
    1. Find the co-ordinates of A¹B¹C¹D¹ 
    2. Draw the quadilateral ABCD and its image A¹B¹C¹D¹ and A²B²C²D² (2 marks)                                         

    3. Hence or otherwise, determine the area of A¹B¹C¹D¹. (2mks)

    4. Another transformation represented by the matrix  maps A¹B¹C¹D¹ onto A¹¹B¹¹C¹¹D¹¹.Draw the image A¹¹B¹¹C¹¹D¹¹. (2mks)

    5. Determine the single matrix, which maps A¹¹B¹¹C¹¹D¹¹ back to ABCD.

22. A particle starts from rest at a point A and moves along a straight line coming to rest at another point B. During the motion, its velocity v(m/s) after time t (sec) is given by v = 9t² − 2t³. Calculate:
    1. The time taken for the particle to reach B. (2 marks)
    2. The distance traveled during the first two seconds. (3 marks)
    3. The time taken for the particle to attain its maximum velocity. (3 marks)
    4. The maximum velocity attained (2 marks)
23.  
    1. Complete the table below for y = sin 2x and y = sin ( 2x + 30) giving values to 2d.p
       

       X°	0	15	30	45	60	75	90	105	120	135	150	165	180
       Sin 2x	0				0.87				− 0.87				0
       Sin (2x +30)	0.5				0.5				− 1				0.5

                                                                                                                                                                                                   (2 marks)
    2. Draw the graphs of y=sin 2x and y = sin (2x + 30) on the axis. (5 marks)                                              
    3. Use the graph to solve Sin ( 2x + 30) − Sin 2x = 0 (1 mark)
    4. State the period and amplitude of y =  Sin (2x + 30) y = Sin(2x + 30) (2marks)
24. A trader makes chairs and tables. The cost of each chair is shs.300 while each table costs shs.700. He is prepared to spend not more than shs. 21,000. It is not viable for him to make less than 20 items. chairs must be less than twice the tables but more than 15. By taking the number of chairs as x and tables as y:
    1. Write down all the inequalities in x and y. (4marks)
    2. Draw the inequalities on the grid provided. (4marks)  
    3. He sells tables at a profit of shs.140 while chairs at a profit of shs.120; Determine the maximum possible profit he makes. (2 marks)

                                                                                MARKING SCHEME

(SECTION I: 50 MARKS)

1. Use logarithms to evaluate. (4marks)
                                
                                                
2. Make x the subject of the formula. (3 marks)
                                     
           y² =  x                                                                                M1 - s.q for both sides
                 x + h                                                                
   y²x + y²h = x
   y²x − x = −y²h                                                                            M1 - isloating x
   x(y² − 1) = y²h
     x =    − y²h                                                                                A1       
              y² − 1                                                                                 
3. Given that   8   = a + b√3 and that a and b are rational numbers, find the values of a and b. (3 marks)
                    4 − 2√3
                                   8(4 + 2√3)           
                            (4 − 2√3)(4 + 2√3)                                            M1 - rational denominators
                             32 + 16√3
                              16 − 12                                                           M1 
                  32 + 16√3
                   4         4                                                                      A1 - for both
                   8 + 4√3
                    a = 8
                    b = 4
4. Given that A = (1 5 3 7 ) and B = ( 7 3 − 4 ) and that C = AB, find C^-1 (3 marks)
                                    
5.  
   1. Expand and simplify (1 + 2x)⁷ up to the term in x³ (2 marks)
                            
   2. Use the expansion in (a) above to estimate the value of (1.02)⁷ correct to four decimal places. (2 marks)
      2x = 0.02     1 + (14 x 0.01) + 84 x (0.01)² + 280 x (0.01)³                    M1
       x = 0.01    = 1 + 0.14 + 0.0084 + 0.00028                                             A1
                        = 1.14868 
                        = 1.1487
6. Solve for x in: log (7x + 2) – log (x – 1) = 0 (3 marks)
        7x + 2 = 1
         x − 1
         7x + 2 = x − 1
                6x = − 3
                  x = − ½
7. Find the quartile deviation for the following set of data (3 marks)
   16, 42, 41, 6, 20, 28, 19, 23, 15
                             
   
8. The radius and height of a cylindrical tank rounded to 1cm are 105cm and 300cm respectively. Calculate the percentage error in its volume. (to 4 s.f) (3 marks)
           Actual volume = ²²/₇ x 105² x 200
                                   = 10395000                                                             M1
           Max volume = ²²/₇ x 105.5² x 300.5
                               = 10, 511, 762.11                                                         M1
            Min volume = 22/7 x 104.52 x 299.5
                               =  10279075.32                                                            A1
           Error = 10511726.11 − 10279075.37
                                             2
           % error = 116325.3943 x 100%
                            10395000                 =  1.119%
9. Give that 25x² − 20x + k is aperfect square. Find the value of K.   (2 marks)
                                          
                                              25K= 100
                                                  K = 4
10. Solve for x in the equation;   (3 marks)
    2Sin²x − 1 = Cos²x + Sin x, for 0° x ≤ 360°                    a = ⁻²/₃ and a = 1                               M1
                     Cos² = 1 − Sin²x                                            Sin x = ⁻²/₃                                                      M1
                      2 Sin²x − 11 = 1 − Sin²x + Sinx              ⇒   x = 41.81° 
                      3 Sin2x − Sinx − 2 = 0                                  x = 221.81°, 318.19°                            A1
                       3a² − a − 2 = 0                                             Sin x = 1
                      (3a +2)(a − 1) = 0                                                x  = 90°
11. P and Q are two points on the earth’s surface. Their positions are P (60°S, 30°E) and Q (60°S, 90° W).Find the distance between P and Q along the parallel of latitude in km (Take radius of earth = 6370 km and π = ²²/₇) [to 1 decimal place.) (3 marks)
                D = 120° x 2 x 22 x 6370 Cos 60°                                            B1 - for 120°
                       360            7                                                                      M1
                D = 6673.333km                                                                       A1
                    = 6673.3km
12.  
    1. The sum of the fifth and sixth term of an AP is 30. If the third is 5, find the first term. (2 marks)
            a + 4d + a + 5d = 30
               2a + 9d = 30                            d = 4                                        M1
                 a + 2d = 5                ⇒          a + (2 x 4) = 5                  
            2a + 9d = 30                              a + 8 = 5                                   A1
          −2a + 4d = 10                                    a = − 3
                     5d = 20
    2. The sum of the first 10 terms of the AP (2 marks)
                                           
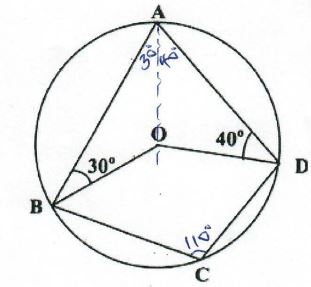
13. In the figure below, ABCD is a cyclic quadrilateral. Point O is the centre of the circle. Angle ABO = 30° and angle ADO=40°
                                                                        
    Calculate the size of angle BCD. (2 marks)
            ∠BAO= 30° & ∠ DAO = 40°                                        B1 - for 30° $ 40° or 70°
              180° − 70° = 110°                                                      B1 - for 110° can be shown on the diagram
14. Obtain the Centre and radius of the circle represented by the equation.   (3 marks)
    x² + y² − 10y + 16 = 0
                 x² + 0x + y² − 10y = − 16                                       M1
                 (x − 0)² + (y − 5)² = −16 + 25                                 M1
                    x² + (y − 5)² = 9
                Cenre = (0, 5)                                                          A1
                radius = 3
15. John bought 3 brands of tea A, B and C.  The cost price of the three brands was sh.25, sh.30 and sh.45 per kilogram respectively.  He mixed the three brands in the ratio 5:2:1 respectively.  After selling the mixture he made a profit of 20%.  How much profit did he make per kilogram of the mixture?                         (4mks)
    

    brands	A	B	C	blend
    Cost per kg	25	30	45	x
    Ratio	5	2	1	8
    Total cost	125	60	45	8x

    
     ²³⁰/₈ = ^8x/₈                             =  34.50                                             M1
    x = 28.75                                = 34.50 − 28.75                                 M1
    B.p = 28.75                    ⇒      = 5.75                                               M1
    28.75 = 100%                                                                                   A1
        ?        120%
16. Draw a line DF= 4. 6cm.Construct the locus of point K above DF such that angle DKF = 70°. (3 marks)
                                                             
    - constant angle has obtaining centre                                                                              B1
    - major arc                                                                                                                        B1
    - showing  ∠ DKF                                                                                                             B1

SECTION II (50 MARKS)

(Answer ONLY FIVE questions in the spaces provided)

17. In the figure below, E is the midpoint of BC. AD : DC = 3:2 and F is the meeting point of BD and AE.
                                      
    1. Express the following vectors in terms of b and c
       
       1.     (2 marks)
                                                     
          
          
       2.       (2 marks)
          
    2. If BF = tBD and AF = nAE, find the value of t and n (5 marks)
       
    3. State the ratio in which F divides BD and AE (1 mark)
       bf = ⁵/₈ BD   5:3 and 3:1  respectively
18. The probability that a boy goes to school by bus is ¹/₃ and by matatu is ¹/₂ . If he uses a bus the probability that he is late to school is ¹/₅ and if he uses a matatu the probability of being late is ³/_10. If he uses other means of transport, the probability of being late is ¹/₂₀.
    1. Represent this information on a tree diagram. (2 marks)
                                                                                B1 - first branch and B1 - 2nd branch
       
       
    2. What is the probability that;
       1. He will be late to school (2 marks)
          (¹/₃ x ¹/₅) + (¹/₂ x ³/₁₀) + (¹/₆ x ¹/₂₀)
          ¹/₁₅ + ³/₂₀ + ¹/₂₀
          ⁹/₄₀
       2. He will not be late to school (2 marks)
          = 1 − ⁹/₄₀
          = ³¹/₄₀
       3. He will be late to school if he does not use a matatu. (2 marks)
            ( ¹/₃ x ¹/₅) + (¹/₆ x ¹/₂₀)
                = ¹/₁₅ + ¹/₁₂₀
                = ³/₄₀
       4. He neither uses a bus nor matatu but arrives to school early. (2 marks)
             ¹/₆ x ¹⁹/₂₀ = ¹⁹/₁₂₀
19. The diagram below represents a cuboid ABCDEFGH in which FG= 4.5 cm, GH = 8cm and HC = 6 cm
                                                              
    Calculate:
    1. The length of FC (2 mks)
                        
    2.  
       1. the size of the angle between the line FC and the plane FGHE (2 mks)
                Tan θ = ⁶/_9.18
                   θ = 33.17°
       2. The size of the angle between the lines AB and FH (2 mks)
                Tan θ = ⁸/_4.5 = 60.64°
       3. The size of the angle between the lines AC and GE (2mks)
                Sin ½ θ = ^2.25/_4.6
                      ½ θ = 29.3°       
                          θ = 58.6°
    3. The size of the angle between the planes ABHE and the plane FGHE (2 mks)
                     Tan θ = 6/8 
                            θ = 36.9°
20. The table below shows the income tax rates
    

    Income per  annum in K£	Rate in Sh per K£
    1-1980	2
    1981-3960	3
    3961-5940	5
    5941-7920	7
    7921-9920	9
    Over 9920	10

    Juma is a salaried employee with a basic salary of Ksh. 15,710 per month and house allowance of sh1,350 monthly. He is also entitled to a monthly tax relief of Ksh1320.
    Calculate:
    1. Juma’s annual salary in K£. (2 marks)
       ( 15, 710 + 1350) = 17, 060
        = 17, 060 x 12
                    20
       = K£ 10, 236
    2. The monthly tax paid by Juma in Ksh. (6 marks)
       1980 x 2 = sh. 3960
       1980 x 3 = sh. 5940
       1980 x 5 = sh. 9900
       1980 x 7 = sh. 13860
       1980 x 9 = sh. 18000
         316 x 10 = sh. 3160
       Gross tax = sh. 54, 820
       54820 
           12    
       sh. 4568.33
          −1320.00
            3248.33
    3. Find his net pay per month in Ksh. (2 marks)
       = 17, 060 − 3248.33
       = 13, 811.67
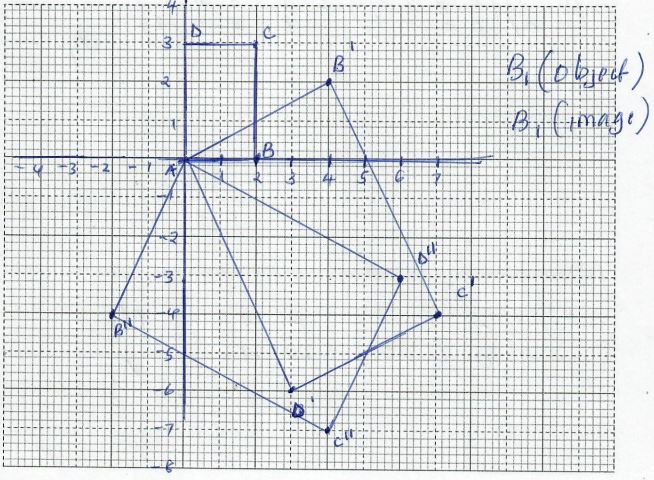
21. A transformation represented by the matrix  to map onto A 0,0) B(2, 0) C(2, 3) and D(0, 3) onto A¹B¹C¹D¹ respectively
    1. Find the co-ordinates of A1B1C1D1
                      
    2. Draw the quadilateral ABCD and its image A¹B¹C¹D¹ and A2B2C2D2 (2 marks)
                                                    

    3. Hence or otherwise, determine the area of A¹B¹C¹D¹. (2mks)
       A.S.F = 5
       Object area = 2 x 3 = 6
       Image area = 6 x 5 = 30 sq. units

    4. Another transformation represented by the matrix  maps A¹B¹C¹D¹ onto A¹¹B¹¹C¹¹D¹¹.Draw the image A¹¹B¹¹C¹¹D¹¹. (2mks)
                                                     

    5. Determine the single matrix, which maps A¹¹B¹¹C¹¹D¹¹ back to ABCD.
                                                   

22. A particle starts from rest at a point A and moves along a straight line coming to rest at another point B. During the motion, its velocity v(m/s) after time t (sec) is given by v = 9t² − 2t³. Calculate:
    1. The time taken for the particle to reach B. (2 marks)
       v = 9t² − 2t³ = 0
             t²(9 − 2t) = 0
                  t = 0
                    or
                 t = 4.5
    2. The distance traveled during the first two seconds. (3 marks)
                     
    3. The time taken for the particle to attain its maximum velocity. (3 marks)
                       a = dv =0 
                             dt
                       18t − 6t² = 0
                          6t (3 − t) = 0
                           t = 0 or t = 3
                           time is 3 seconds
    4. The maximum velocity attained (2 marks)
       t = 3
       Max velocity = 9 x 9 − 2 x 27
                            = 81 − 54 
                            = 27m/s
23.  
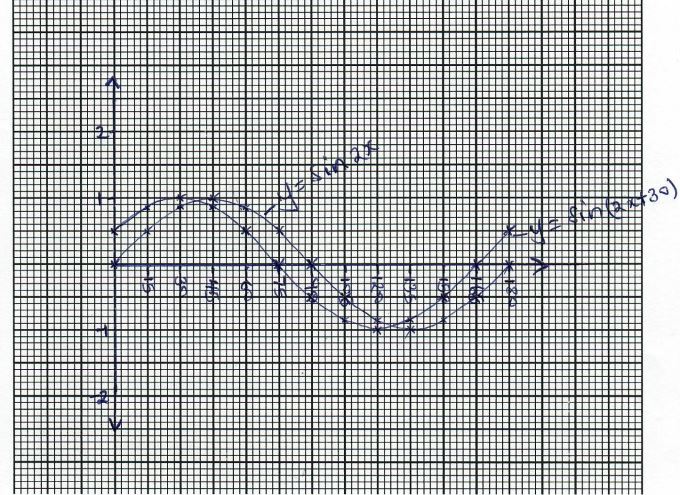
    1. Complete the table below for y = sin 2x and y = sin ( 2x + 30) giving values to 2d.p
       

       X°	0	15	30	45	60	75	90	105	120	135	150	165	180
       Sin 2x	0	0.5	0.87	1.00	0.87	0.5	0.00	− 0.5	− 0.87	−1.00	− 0.87	− 0.50	0
       Sin (2x +30)	0.5	0.87	1	0.87	0.5	0	−0.50	− 0.87	− 1	− 0.87	− 0.50	0	0.5

                                                                                                                                                                                                   (2 marks)
    2. Draw the graphs of y=sin 2x and y = sin (2x + 30) on the axis. (5 marks)
                                                     
    3. Use the graph to solve Sin ( 2x + 30) − Sin 2x = 0 (1 mark)
       x = 37.5° ± 1.5°
                 or
       127.5 ± 1.5°
    4. State the period and amplitude of y = Sin( 2x + 30) y = Sin (2x + 30) (2marks)
         A = 1
         P  = 360°
                   2       = 180°
24. A trader makes chairs and tables. The cost of each chair is shs.300 while each table costs shs.700. He is prepared to spend not more than shs. 21,000. It is not viable for him to make less than 20 items. chairs must be less than twice the tables but more than 15. By taking the number of chairs as x and tables as y:
    1. Write down all the inequalities in x and y. (4marks)
       300x + 700y ≤ 21,000
       x + y ≥ 20
       x ≤ 2y
       x ≥ 15
    2. Draw the inequalities on the grid provided. (4marks)                                           
    3. He sells tables at a profit of shs.140 while chairs at a profit of shs.120; Determine the maximum possible profit he makes. (2 marks)
       To determine the maximum profit, you'll need to find the corner point within the shaded region that maximizes the profit. This corner point is the solution to the system of inequalities. Calculate the profit at each corner point (intersection of the lines), and the maximum profit will be the highest profit among these points.
       Profit from selling chairs = 120x
       Profit from selling tables = 140y