MATHEMATICS
PAPER 1
INSTRUCTION TO CANDIDATES:
- This paper consists of two Sections; Section I and Section II.
- Answer ALLthe questions in Section I and any five questions from Section II.
- Show all the steps in your calculation, giving your answer at each stage in the spaces provided below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.
- andidates should check the question paper to ascertain that all the pages are printed as indicated
and that no questions are missing. - Candidates should answer the questions in English.

Questions
SECTION I:(50 MARKS)
Answer all the questions in this section.
- Evaluate without using mathematical tables. (3mks)
1.9 x 0.032
20 x 0.0038 - Use tables of reciprocals only to find the value of (3mks)
5 - 14
0.0829 0.581 - You are given that cos θ= 8/10 . Without using mathematical tables express in fraction form the value of
- Sin θ (2mks)
- tan (90 - θ) (1mks)
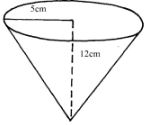
- An open right circular cone has radius of 5cm and a perpendicular height of 12cm .
Calculate the surface area of the cone correct to 1 decimal place.(Take π to be 3.142) (3mks) - Nyongesa spends a total of sh.970 on buying three text books and five pens. If he had bought two text books and five pens he would have saved sh.90. Find the cost of one text book. (3mks)
- A Kenyan tourist left Germany for Kenya through Switzerland. While in Switzerland he bought a watch worth 52 Deutche marts. 1 swiss Franc = 1.28 DM and 1 Swiss Franc = 45.21 Kenya shillings.
Find the value of the watch in;- Swiss Franc (2mks)
- Kenya shillings using the exchange rates above. (2mks)
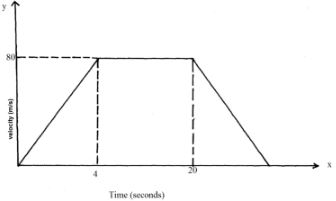
- The figure below is a velocity –time graph for a car that was in motion for 24 seconds.
- Find the total distance traveled by the car? (2mks)
- Calculate the deceleration of the car. (2mks)
- Form the quadratic equation whose roots are x= - 5/3 and x=1 in the form ax2 +bx+c=0. (2mks)
- Three towns are situated in such a way that town B is 40km due south of town A and town C is 30 km due East of town B.
- Draw a sketch diagram showing the position of town A.B and C. (1mk)
- From your sketch, calculate:
- Distance AC (1mk)
- To the nearest degree the bearing of town A from town C. (2mks)
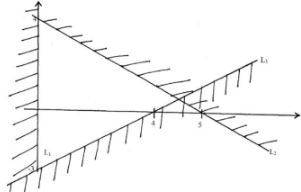
- Find the inequalities that defines the region R shown in the figure below (3mks)
- The interior angle of a regular polygon is 20º more than three times the exterior angle. Determine the number of sides of the polygon. (3 marks)
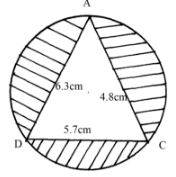
- The circle below whose area is 18.05cm2 circumscribes a triangle ABC where AB=6.3cm, BC =5.7cm and AC =4.8cm. Find the area of the shaded part. (3mks)
- Solve for x in the equation. (3mks)
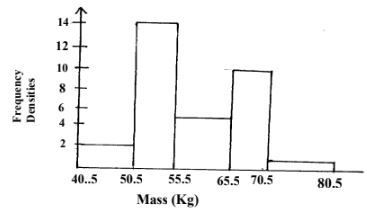
9(x-1) x 3(2x+1) = 243 - The graph below shows frequency densities for the masses of some 200 students selected from a class. Use it to answer the questions that follow:
- Complete the frequency distribution table below (2mks)
Mass in (Kg) Frequency - State the modal frequency (1mk)
- Complete the frequency distribution table below (2mks)
- The volumes of two similar solid cylinders are 4752 cm3 and 1408 cm3 .If the area of the curved surface of the smaller cylinder is 352 cm2 , find the area of the curved surface of the larger cylinder (3mks)
- The line which joins the point A (3, K) and B (-2, 5) is parallel to the line whose equation is 5y+2x- 7=0. Find the value of K. (3mks)
SECTION II (50 MARKS)
Answer only five questions in this section in the spaces provided.
- John bought 3 brands of tea, A B and C. The cost price of the three brands were sh 25, sh 30, sh 45 per kg respectively. He mixed the three brands in the ratio 5:2:1 respectively: After selling the mixture he made a profit of 20%.
- How much profit did he make per kilogram of the mixture? (4 mks)
- After one year the cost price of each brand was increased by 10%
- For how much did he sell one kilogram of the mixture to make a profit of 15%? (Give your answer to the nearest 5 cents) (3 mks)
- What would have been his percentage profit if he sold one kilogram of the mixture at sh. 45. (3 mks)
- The equation of a curve is given as y=2x3 - 9/2x2 -15x+3
- Find:
- the value of y when x=2 (2 marks)
- the equation of the tangent to the curve at x=2 (4 marks
- determine the turning points of the curve (4 marks)
- Find:
-
- Using the trapezium rule with 7 ordinates, estimate the area of the region bounded by the curve y=- x2 +6x+1, the lines x=0, y=0 and x=6. (5mks)
- Calculate :
- The area of the region in (a) above by the integration; (3mks)
- The percentage error of the estimated area to the actual area of the region, correct to 2 decimal places. (2mks)
- A country bus left town A at 11.45 am and traveled towards town B at an average speed of 60km/h.Amatatu left town B at 1.15 pm on the same day and traveled towards town A along the same road at an average speed of 90km/h. the distance between the two towns is 540km. Determine
- The time of day when the two vehicles met (4mks)
- How far from town A did they meet ? (2mks)
- How far outside town B the bus was when the matatu reached town A (4mks)
- A straight line passing through the points (8,-2) and (4,-4) has its equation in the form ax + by + c = 0, where a, b and c are integers.
- Determine the numerical values of a, b and c. (3mks)
- If the line in (a) above cuts the x-axis at point P, determine the coordinates of P. (2mks)
- Another line, which is perpendicular to the line in (a) above passes through point P and cuts the y axis at Q. determine the coordinates of point Q. (3mks)
- Find the length of QP (2mks)
-
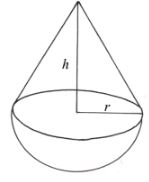
- The figure below shows a metal solid consisting of a right cone mounted onto a hemisphere. The height h of the cone is twice the radius r. if the volume of the solid is 36cm3 , find the radius of the hemisphere. (4mks)
- The solid is totally immersed in water contained in a cylindrical tin of radius 9cm. Through what height does the water level in the tin rise? (2mks)
- The solid is melted and recast into a right pyramid of vertical height 4.2cm. Find the base area of the pyramid. (2mks)
- If the solid is of mass 14.4g. Find its density in kg/m3. (2mks)
- The figure below shows a metal solid consisting of a right cone mounted onto a hemisphere. The height h of the cone is twice the radius r. if the volume of the solid is 36cm3 , find the radius of the hemisphere. (4mks)
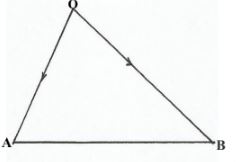
- In the diagram below, AOB is a triangle such that OA = a, OB = b and <AOB is obtuse.
If P is a point on AB such that AP = 3PB and Q is the mid-point of OA- Express in terms of a and b
- AB (1mk)
- BQ (2mks)
- If X is a point on BQ such that BX =hBQ, express OX in terms of a b and h, where h is a scalar. (3mks)
- Given further that OX = kOP where k is another scalar, obtain the values of h and k. (4mks)
- Express in terms of a and b
- The table below shows the length of 40 seedlings.
DetermineLength in (mm) Frequency 118-126 3 127 – 135 4 136 – 144 10 145 – 153 12 154 – 162 5 163 – 171 4 172-180 2 -
- The modal class (1 Mark)
- The median class (2 mks)
-
- The mean of the seedlings (4 mks)
- The median of the seedlings (3 mks)
-

Marking Scheme
- 1.9 x 0.032 x 10000
20 x 0.0038 x 10000
19 x 32
20 x 38
16/20
8/10
- 5 x 1 - 14 x 1
8.29 x 10-2 5.81 x 10-1
5 x 0.1206 x 102 -14 x 0.1721 x 10
=60.3-24.094
=36.206 - Cos = Ads = 8
hps 10
QR=8 and PQ=10
PR2 =PQ2 -QR2 =102 -82
PR=√36 = 6- sin θ = 6/10 or 3/5
- tan (90-θ) =QR/PR = 8/6 or 4/3
-
SA= πrl
1= √52 +122
= √169
=13cm
=3.142x13x5
=188.5 - Let cost of text bk be t and pen p.
3t +5p = 970.......(i)
2t + 8p = 880.......(ii)
Multiply e.g(i) by 8 and (ii0 by 5
24t + 40p = 7760
10t+40p=4400
14t=240
Cost of 1 text bk=sh.240 -
- 1.28 Deutche marks=1 Swiss franc
52 Deutche marks =?
52 x swiss franc
1.28 Deutche marks
=40.635
≈40.63 Swiss francs - I swiss franc =42.21Ksh.
40.63 Swiss franc=?
42 .21 x 40.63
1
=1,714.99 Kenya shillings
- 1.28 Deutche marks=1 Swiss franc
-
- Dist= 1⁄2 x 4 x 80 + 80 x 16 + 1⁄2 x 4 x 80
=160+1280+160
=1600m - Deceleration= 0-80/4 = 20m/s2
- Dist= 1⁄2 x 4 x 80 + 80 x 16 + 1⁄2 x 4 x 80
- Soln:x= -5/3 and x=1
= -5 and x=1
∴ (3x+5)(x-1)=0
3x(x -1)+5(x-1)=0
3x2 -3x+5x -5=0
3x2 +2x -5=0 -
- Diag,
Bearing of A from C
=270+ θ -
- AC2 =AB2 +BC2 =402+302
=√ 2500
=50km - sin θ = 40/50 = 0.8
θ =53.13
≈ 53º
- AC2 =AB2 +BC2 =402+302
- Diag,
- L1 = x>0
L2 = x/5 + y/4 =1
4x + 5y = 20
4x + 5y < 20
L3: x/4 + y/-3 = 1
3x - 4y=12
∴3x -4y <12
- Let ext. < xº
Interior < = 3x + 20º
4x = 160º
4x = 160º
x = 40
360/40= 9 sides -
s = √s(s-a)(s-b)(s-c)
s = 1/2(4.8 + 6.8 + 5.7)= 8.4
Area = √8.4(2.7)(3.6)(2.1)
18.05 - 13.0943
= √171.4608
= 13.0943
=4.9557
≈4.96 - Change to base 3
32(x-1) x 3(2x+1) =35
2(x-1)+2x+1=5
2x-2=2x+1=5
4x-1=5
4x=6
x=1.5 -
Mean in kg 41-50 51-55 56-65 66-70 71-80 Frequency 20 70 50 50 10 - Modal frequency is 70.
- L.S.F=V.S.F
lsf= √4752/1408
=1.5
l.s.f2 =A.S.F
1.52 = Area of larger cylinder
352
Area of larger cylinder 792cm2 - Reduce 5y+2x=7 in the form y=mx+c
∴ y= -2/5x + 7/5
But gradient =
k-5 = k-5
3-2 5
k-5 = 2
5 3
k=3 -
- 5 x 25 + 2 x 30 + 45 x 1 = 28.75
8
Profit 28.75 x 20/100 = sh5.75 -
- New price = 28.75/100 x 110 x 115/100 = 36.40
- 28.75 x 110/100 = 31.60
New profit 45 - 31.60 x 100
31.60
= 13.4 x 100
31.60
=42.41%
- 5 x 25 + 2 x 30 + 45 x 1 = 28.75
-
X -3 -2 -1 0 1 2 3 4 X2 9 4 1 0 1 4 9 16 2X2 18 8 2 0 2 8 18 32 -3X 9 6 3 0 -3 -6 -9 -12 -5 -5 -5 -5 -5 -5 -5 -5 -5 Y 22 9 0 -5 -6 -3 4 15
minimum at point(1,6)
y= 2 x 2 - 5x -5
0= 2 x 2 - 3x - 5
Y=0
X=-1 or x=2.5
y= 2x2 - 3x -5
0= 2 x 2 -5x -3
Y= 2x -2
X= 0.5 or x=3 -
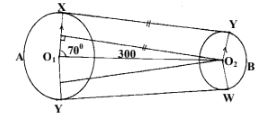
- XV=MO2 = 300sin 70 = 281.9cm
- YBW = 140/360 x 2πr
MO1 = 300 Cos 70 = 102.6cm
Radius of small circle = 180 - 102.6 = 77.4cm
VBW = 140/360 x 2 x 3.142 x 77.4 = 189.1cm - XAY = 220/360 x 2π x 180
= 220/360 x 2 x 3.142 x 180 = 691.2cm - Length of conveyor belt
= 281.9 x 2 + 189.1 + 691.2
=1444.1cm2
- XV=MO2 = 300sin 70 = 281.9cm
-
- 11.45 = 11/2h
Distance moved by bus = 1.5 x 609 = 90km
Distance between 2 vehicles
540 - 90=450
R. speed = 60 + 90 = 150km/h
T.taken to meet = 450 ÷ 150 = 3h
= 1.15 + 3 = 4:15pm - Total time moved by bus when they meet
16:15 - 11:45 = 41/2
Distance from A = 4.5 x 60 = 270km - Time taken by matatu to travel from B to A = 540 ÷ 90 =6
∴ Time matatu reaches A
13:15 + 6 = 19:15hrs
∴Time travelled= 19:15-11:45 = 71/2 hrs
distance = A= 7.5 x 60
Hence:
540 - 450 = 90km
- 11.45 = 11/2h
-
- y + 2 = -4 + 2 = 1
x-8 4-8 2
2y + 4 = x -8
⇒ x - 2y - 12 = 0
∴ u =1, b= -2 and c= -12 - y = x/2 -6 , when y=0
x/2 - 6= 0 ⇒ x=12
∴ coordinates of pane (12,0) - y = -2
x -12
⇒ y = 24 - 2x
but when x = 0, y=24 - ∴ coordinates of q are(0,24)
QP = √(12-0)2 + (0-24)2
=√144 + 576 = 26.83 units
- y + 2 = -4 + 2 = 1
-
- Volume of solid =volume of cone + vol of hemisphere
=1/3πr2h + 1/2x4/3πr3 = 36
= 1/3πr2 + 2/3πr3=36
=4/3πr3= 36
r3 = 36 x 3
4 x 3.142
r3 = 8.593
r= 2.048cm - Let the level rise be x
πr2x = 36
x = 36
3.142 x 81
36 = 0.14cm
254.502 - Volume = 1/2 Ah
= 1/3 x A x 4.2 = 36
A = 36 x 3
4.2
= 25.71cm2 - Density = mass/ volume
= 14.4/36 x 1000kg/m3
= 400kg/m3
- Volume of solid =volume of cone + vol of hemisphere
-
-
- AB = b - a
BQ = BO = OQ = 1/2 a - b - BX = h(1/2 a - b)
OX = b + h (1/2 a - b)
1/2ha + (1-h)b
- AB = b - a
- OX = ROP
but OP = 1/4a + 3/4b= 1/4(a +3b)
OX = R/4 (a + 3b)
OX = OX2
1/2ha + (1-h)b = 1/4Ra = 3/4kb
1/2h = 1/4⇒(-4-3h= -4)
4h-2k=0
4h-3k=-4
-5k=-4
k=4/5
h=2/5
-
-
Length
(cm)Mid pt
(x)F xf CF 118-135 122 3 366 3 127-135 131 4 524 7 136-144 140 10 1400 17 145-153 149 12 1788 29 154-162 158 5 790 34 163-171 167 4 668 38 172-180 176 2 352 40 40 5888 -
- Modal class ⇒145-153
- Median class 145 -153
-
- Mean of feeding
X= Σxf/Σf
= 5888/40
= 147.2 - Median = L( (ⁿ ⁺ ¹)/₂ - c/f) i
= 144.5 + ((⁴¹/₂ - 17)/12)9
=144.5 + 20.5 - 17 x 9
12
144.5 + 2.625
=147.125
- Mean of feeding
-
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - Royal Exam Series Post Mock Trial Exams 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students