Mathematics Paper 2 Questions and Answers - Royal Exam Series Post Mock Trial Exams 2022

MATHEMATICS
PAPER 2

INSTRUCTIONS:

• Write your name, class and Adm. Number in the space provided above.
• Sign and write the date of examination in the spaces provided above.
• This paper consist of two sections 1 and II.
• Answer all the questions in section 1 and only five questions from section II
• All answers and working must be written on the question paper in the spaces provided below each question.
• Show all the steps in your calculation, giving your answers at each stage in the space provided.
• Marks may be given for correct working even if the answer is wrong.
• Non programmable silent electronic calculator and KNEC Mathematical table may be used, except where stated otherwise.
• Candidates should check the question paper to ascertain that all the pages are printed as indicated and that no questions are missing.

Questions

SECTION I:(50 MARKS)

1. Evaluate without using Mathematical tables or a calculator. (3mks)
   2log5 - ½log6 + 2log 40
2. Under transformation  , The triangle FGH 21cm2 is transformed to F1G Calculate the area of F1G1H1 (3 mks)
3. Make d the subject of the formula. (3mks)
   a² = √ ^1+d²/_b² - ^b/₃
4. Simplify ³/_√7-2 + ¹/_√7  leaving your answer in the form a + b√c, where a, b and c are rational numbers. (3mks)
5. Calculate the percentage error in the volume of a cone whose radius is 9.0cm and slant length 15.0cm. (3mks)
6. A quantity A is partly constant and partly varies inversely as a quantity B. Given that A = -10 when B= 2.5 and A = 10 when B = 1.25, find the value of A when B = 1.5.(4mks)
7. Find the centre and radius of the circle whose equation is 2x²+ 2y²– 8x + 12y – 2 = 0 (3mks)
8. 14 people can build 10 huts in 30 days. Find the number of people working at the same rate that will build 18 similar huts in 27 days. (2mks)
9. The coordinates of two airports M and N are (60ºN, 35ºW) and (60ºN, 15ºE) respectively.
   Calculate;
   1. The longitude difference. (1mk)
   2. the shortest time an aeroplane whose speed is 250 knots will take to fly from M to N along a circle of latitude (2mks)
10.             
    1. Expand (x - 0.2)⁵ in ascending powers of x. (2mks)
    2. Use your expansion up to the fourth term to evaluate 9.8⁵.(2mks)
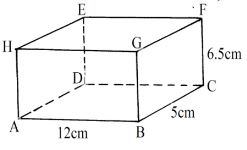
11. The figure below is a cuboid ABCDEFGH. AB = 12cm, BC = 5cm and CF = 6.5cm.
    
    
    1. State the projection of AF on the plane ABCD. (1mk)
    2. Calculate the angle between AF and the plane ABCD correct to 2 decimal places. (3mks)
12. Solve for x in the equation
    2Sin² x - 1 = Cos² x + Sinx for 0 < x <360 (3mks)
13. The mid-point of AB is (1,-1.5, 2) and the position vector of a point A is - i + j .Find the magnitude of AB where O is the origin. (3mks)
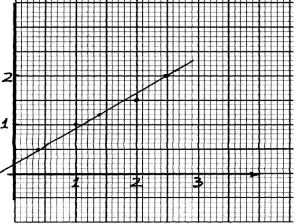
14. Draw a line of best fit for the graph of y against x using the values in the table below.
    Hence determine the equation connecting y and x.
    

    x	0.4	1.0	1.4	2.0	2.5
    y	0.5	1.0	1.2	1.5	2.0

15. A coffee dealer mixes two brands of coffee, x and y to obtain 40kg of the mixture worth Ksh. 2,600. If brand x is valued at Ksh. 70 per kg and brand y is valued at Ksh. 55 per kg. Calculate the ratio in its simplest form in which brands x and y are mixed. (4mks)
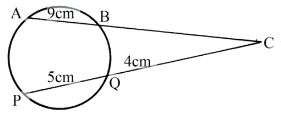
16. The figure below shows a circle centre O. AB and PQ are chords intersecting externally at a point C. AB = 9cm, PQ= 5cm and QC = 4cm. Find the length of BC. (3mks)
    

SECTION II : (50 MARKS)
Answer only five questions in this section

17.        
    1. Salome invested Ksh. 250,000 for 2 1⁄2 years in an account which paid 16% compound interest p.a. The interest is compounded quarterly. At the end of 2 1⁄2 years she withdrew all the amount and spent it to the nearest thousands to buy four similar motor cycles. She earned an average of Ksh. 10,000 from each motorcycle per month.
       Calculate:
       1. the amount she withdrew at the end of 2 1⁄2 years. (2mks)
       2. the cost of each motorcycle. (2mks)
       3. the total earnings from the motorcycles for 3 years. (2mks)
    2. She decided to sell the motorcycles after depreciating at an average rate of 20% p.a for the 3 years.
       Find:-
       1. the new value of each motorcycle after depreciation. (2mks)
       2. the profit earned from her initial investment to the nearest shilling.(2mks)
18. The table below shows the distribution of ages in years of 50 adults who attended a clinic:-
    

    Age	21-30	31-40	41-50	51-60	61-70	71-80
    Frequency	15	11	17	4	2	1

    
    
    1. State the median class (1mk)
    2. Using a working mean of 45.5, calculate:-
       1. the mean age (3mks)
       2. the standard deviation (3mks)
       3. Calculate the 6th decile. (3mks)
          
          
19. An arithmetic progression (AP) has the first term a and the common difference d.
    1. Write down the third, ninth and twenty fifth terms of the AP in terms of a and d. (1mk)
    2. The AP above is increasing and the third, ninth and twenty fifth terms for the first three consecutive terms of a Geometric Progression (G.P) The sum of the seventh and twice the sixth terms of the AP is 78. Calculate:-
       1. the first term and common difference of the AP. (5mks)
       2. the sum of the first nine terms of the AP. (2mks)
       3. The difference between the fourth and the seventh terms of an increasing AP. (2mks)
          
          
20. The probability that three candidates;Anthony,Beatrice and Caleb will pass an examination are ³/₄, ²/₃ and ⁴/₅ respectively. Find the probability that:-
    1. all the three candidates will pass (2mks)
    2. all the three candidates will not pass. (2mks)
       1. only one of them will pass (3mks)
       2. at most two of them will pass. (3mks)
21. Complete the table below for the function y = 3cos x and y = sin2x. (2 mks)
    

    xº

    -180º

    -150º

    -120º

    -90º

    -60º

    -30º

    0º

    30º

    60º

    90º

    120º

    150º

    180º

    2xº

    -360

    -300

    -180º

    180

    240

    3cosx

    Sin2xº

    0.0

    0.9

    -0.9

    
    
    1. On the same axes, draw the graph of y = 3cosx and y = sin2xº for -180º ≤ x ≤ 180º (5 mks)
    2. Use the graph in (b) above to find
       1. The values of x such that 3cosx –sin2x = 0. (2 mks)
       2. The period of y = sin2x (1 mk)
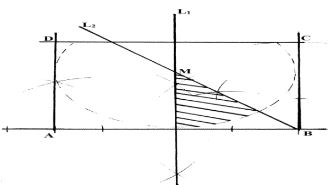
22. Use a ruler and a pair of compasses only all constructions in this question.
    1. Construct the rectangle ABCD such that AB = 7.2cm and BC = 5.6cm. (3mks)
    2. Constructs on the same diagram the locus L1 of points equidistant from A and B to meet with another locus L2 of points equidistant from AB and BC at M.
       Measure the acute angle formed at M by L1 and L2. (3mks)
    3. Construct on the same diagram the locus of point K inside the rectangle such that K is less than 3.5cm from point M. Given that point K is nearer to B than A and also nearer to BA than BC, shade the possible region where K lies.
       Hence calculate the area of this region. Correct to one decimal place.(4mks)
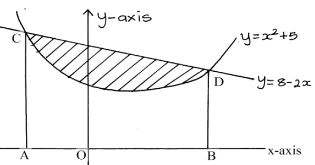
23. The diagram below, not drawn to scale shows part of the curve y = x² + 5 and the line y = 8 - 2x. The line intersects the curve at points C and D. Lines AC and BD are parallel to the y-axis.
    
    
    1. Determine the coordinates of C and D. (4mks)
    2. Use integration to calculate the area bounded by the curve ,the lines AC ,BD and the x-axis between the points C and D. (3mks)
    3. Calculate the area enclosed by the lines CD, CA, BD and the x-axis. (3mks)
    4. Hence determine the area of the shaded region. (1mk)
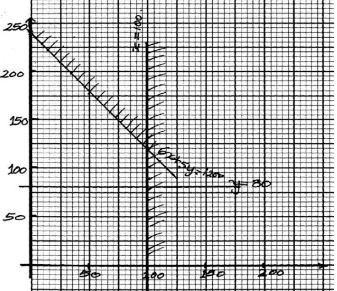
24. A tailoring business makes two types of garments A and B. Garment A requires 3 metres of material while garment B requires 2 1⁄2 metres of material. The business uses not more than 600 metres of material daily in making both garments. It must make not more than 100 garments of type A and not less than 80 Garments of type B each day.
    1. Write down three inequalities from this information other than x > 0 and y > 0 , where x is the number of garments of type A and y the number of garments of type B. (3mks)
    2. Graph these inequalities. (3mks)
    3. If the business makes a profit of sh 80 on garment A and a profit of sh. 60 on garment B, how many garments of each type must it make in order to maximize the profit ,hence determine the maximum profit? (4mks)

Marking Scheme

1. = log 5² - log16^1/2 + log 40 ²
   = log 25 - log 4 + log1600
   = log (^{25 x 1600}/₄)
   = log 10,000
   =4
   
   
2. 2 x - (x - 3) = 0
   2x - x + 3=0
   x=-3
   
   
3. a⁴ =   1+d² +   b  
             b²          3
   a⁴ - ^b/₃ =  1+ d²
                     b²
   b² ( a⁴ - ^b/₃) = 1+d²
   b²(a⁴ - ^b/₃) -1=d²
   d=√b²(a⁴ - ^b/₃) -1
   
   
4.  = 3√7 + √7 - 2
       √7 (√7 -2)
   = 4√7 -2
      7-2√7
   =   4√7 - 2  x  7 +2√7 
       7 - 2√7      7+2√7
   = 4√7 +(7+2√7) - 2(7+2√7)
                  21
   28√7 + 56 - 14 -4√7
             21
   42 + 24√7
        21
   2 + ⁸/₇√7
   
   
5. Height = √152 - 92 = 12.0cm
   v= 1/3 x π x 9.0 x 9.0 x 12.0
   %error = (^0.05/_9.0 + ^0.05/_9.0 + ^0.05/_12.0) x 100
   =1.528%
6.  
   A = k + m/B
   -10 = k + m/2.5
   -25 + 2.5k + m
   10=k + m/1.25
   12.5 = 1.25k + m
   -25 = 2.5k + m
   12.5 = 1.25k + m
   -37.5 = 1.25k
   k= -30
   12.5 = 1.25(-30) + m
   m=50
   A= -30 + 50/B
   =-30 + 50/1.5
   3 1/3
   
   
7. Area = h(y₁ + y₂ ........)
   =0.4(6.2 + 4.3 + 2.6)
   =5.24
              
8. = 14 x ¹⁸/₁₀ x ³⁰/₂₇
   =28
   
   
9.          
   1. 35 + 15 = 50º
   2. Time = 60 x 50 x cos60
                        250
      =6hrs
10.          
    1.  = x⁵ + 5x⁴(-0.2) + 10x³(-0.2)2 + 10x²(-0.2)2 + 5x(-0.2)4
       = x⁵ - x⁴ + 0.4x³ - 0.08x² + 0.008x - 0.00032
       
       
    2. = 10⁵ - 10⁴ + 0.4(10)³ - 0.08(10)²
       = 90392
11.                   
    1. AC
    2. AC = √12² + 5² = 13cm
       tan θ = 6.5/13
       θ = 26.57º
       
       
12.  sin x cos x + sin x
       cos x          cos x
    = sin x + tan x
    
    
13. A(-1,1,0)   B(x,y,z)
    ⇒ -1 + x = 1, 1 + y = -1.5, 0 + z = 2
           2                2                  2
    x=3, y=-4, z=4
    B(3, -4, 4)
    /OB/ = √3² + (-4)² + 4²
    =√41
    = 6.403
    
    
14.     
    
    y= 0.7x + 0.2
    
    
15. 2600/40 = 65
    
    2:3
    
    
16. x(x+9)=36
    x² + 9x - 36 = 0
    (x+12)(x-3)=0
    x=-12, x=3
    BC=3cm
    
    
17.         
    1.     
       1. 250,000(1 + 4/100)10
          =sh370061.0712
          
          
       2. 370,000/4
          = sh92,500
          
          
       3. 10,000 x 4 x 36
          = sh 1 440 000
    2.                    
       1. 92500(1 - 20/100)3
          = 47360
          
          
       2. Profit = (61 + 1 440 000 + 189 440) - 250 000
          = 1 379 501
18.    
          

    Class	x	tx -45.5	f	ft	ft2	cf
    21-30 31-40 41-50 51-60 61-70 71-80	25.5 35.5 45.5 55.5 65.5 75.5	-20 -10 0 10 20 30	15 11 17 4 2 1	-300 -110 0 40 40 30	6000 1100 0 400 800 900	15 26 43 47 49 50
    			50	-300	9200

        
    1.   31-40   
    2.           
       1. Mean = -300/50 + 45.5
          = 39.5yrs
       2. s.d = √⁹²⁰⁰/₅₀ - (-³⁰⁰/₅₀)²
          = 12.17
    3. 6th = 40.5 + ( 30 -26) 10
                                 17
       = 42.85
19.                    
    1. a + 2d , a + 8d , a + 24d
    2.         
       1. a + 8d   a + 24d
                     =                                  I
          a + 2d    a + 8d
          a + 6d + 2(a + 5d)= 78          II
          
          16d = 10a                   I
          3a + 16d =78             II
          
          3a + 10a = 78
          13a=78
          a=6
          16d = 10 x 6
          d = 3.75
          
          
       2. S_q = 9/2 ( 2 x 6 + (9-1)3.75) 
          =189
          
          
       3. ⇒[ 6 + 6(3.75)] - [6+3(3.75)]
20.  P(A) = 3/4   P(A')= 1/4
    P(B) = 2/3    P(B') = 1/3
    P(C) = 4/5   P(C') = 1/5
    
    
    1. P(ABC) = 3/4 x 2/3 x 4/5
       = 2/5
       
       
    2. P(A'B'C') = 1/4 X 1/3 X 1/5 
       = 1/60
       
       
    3. ⇒P(A'B'C' or A'BC'  A'B'C)
       =(3/4 x 1/3 x 1/5) + ( 1/4 x 2/3 x 1/5) + ( 1/4 x 2/3 x 4/5)
       =9/60
       
       
    4. ⇒P(ABC' or AB'C or A'BC)
       =( 3/4 x 2/3 x 1/5) + (3/4 x 1/3 x 1/5) + (1/4 x 2/3 x 4/5)
       = 26/60
       
       
    5. ⇒ 1 - P(ABC)
       = 1 - 2/5
       = 3/5
21.                
    1. 
       

       x
       x+1			0		2			5
       3-x				3			0
       y			0			3

    2.     
       
    3.            
       1. (3-x)(x+1)=0
          -x² + 2x + 3 =0   x=3, -1
          
          
       2. -x² + 2x + 3 = y
          -x² + x + 6 = 0
          x-3=y    x=-2, 3
22.              
    
    ⁴⁴/₃₆₀ x ²²/₇ x 3.5 x 3.5
    = 4.7cm²
    
    
23.             
    1. x2 + 5 = 8 - 2x
       x2 + 2x - 3 = 0
       (x+3)(x-1)=0
       x=-3 or 1
       when x=-3, y=14
       When x =1 , y=6
       coordinates
       C(-3,14) and D(1,6)
       
       
    2.  _-3∫¹( x² + 5)dx
       =[ ^x³/₃ + 5x + c]³₁
       =(¹/₃ + 5) - ( ^-3³/₃ +5(-3))
       =32 ¹/₃ square units
       
       
    3. Area under line y=8-2x
       =(8x - ^2x²/₂) ¹_-3
       = (8(1)-12) - (8(-3)-(-3)2)
       =40
    4. Shaded area = 40 -32¹/₂
       = 7 ²/₃
24.  3x 2.5y < 600
    x < 100
    y > 80
    
    Solution (100, 120)
    100type A and 120 type B garments
    Profit=80 x 100 + 60 x 120
    =sh. 15, 200