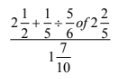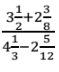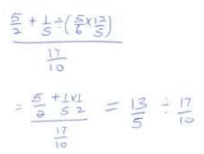Mathematics Questions And Answers - Form 1 Term 2 Opener 2021

INSTRUCTIONS TO CANDIDATES

This paper consists of two Sections; Section I and Section II.
Answer ALL the questions in Section I and only five questions from Section II.
All answers and working must be written on the question paper in the spaces provided below each question.
Show all the steps in your calculation, giving your answer at each stage in the spaces provided below each question.
Marks may be given for correct working even if the answer is wrong.
KNEC Mathematical tables may be used, except where stated otherwise.
Candidates should answer the questions in English.

SECTION I

Without using a calculator evaluate leaving the answer as a fraction in its simplest form (3 marks)
A farmer distributed his bags of cabbages as follows:
A certain hospital received a quarter of the total number of bags. A nearby school received half of the remainder. A green grocer received a third of what the school received. What remained was six more than what the green grocer received. How many bags of cabbages did the farmer have? (3mks)
Simplify the expression
5a – 4b – 2 [a –(2b + c)] (2 marks)
Evaluate: −12÷(−3)×4−(−20) (3 marks)
−6×6÷3+(−6)
All prime numbers less than ten are arranged in descending order to form a number. (a)
1. Write down the number formed (1 mark)
2. State the total value of the second digit in the number formed in (a) above (2 mks)
A fruit vendor bought 1948 oranges on a Thursday and sold 750 of them on the same day. On Friday, he sold 240 more oranges than on Thursday. On Saturday he bought 560 more oranges. Later that day, he sold all the oranges he had at a price of Ksh 8 each.
Calculate the amount of money the vendor obtained from the sales of Saturday. (4 marks)
A rectangle of side 48cm by 60cm is divided into squares of side X cm. Find the greatest value of X and find the area of the square. (3mks)
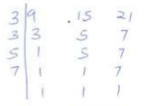
Three bells rang at intervals of 9minutes, 15 minutes and 21minutes. The bells will ring together at 11.00p.m.Find the time the bells had last rang together (3 marks)
Three businessmen Makokha, Njau and Odhiambo contributed a total amount of sh 120,000 to start a business. The ratio of the contributions of Makokha and Njau was 2:3 and that of Njau to Odhiambo was 2:5. How much did Odhiambo contribute? ( 4 marks)
Two pairs of trousers and three shirts cost a total of 390. Five such pairs of trousers and two shirts cost a total of sh.810. Find the price of a pair of trousers and a shirt. (3marks)
Solve the equation ¹/_4x = ⁵/_6x − 7 (3 marks)
Without using mathematical tables evaluate (3 marks)
0.18 ×4
√(3.24 ×4)
A number n is such that when it is divided by 27, 30,or 45, the remainder is always 3. Find the smallest value of n. (3mks)
1. The prime numbers between 30 and 40 are written in ascending order to form a number. Write down the number. (1mk)
2. A second number is formed by writing all square numbers between 40 and 70 in the ascending order. Find the difference between this number and the one formed in (a) above giving your answer to the nearest tens. (2mks)
A watch which looses a half a minute every hour was set read the correct time at 0445hr on Monday. Determine in twelve hour system the time the watch will show on Friday at 1845hr the same week. 3mks
Arrange the following fractions in ascending order. ²/₃ , ⁷/₁₂ , ⁵/₈, (3mks)

SECTION II
Answer only FIVE questions from this section

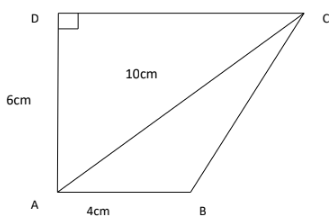
In the figure below AB=4cm, AD=6cm and AC=10cm find:
1. the area of triangle ABC. (3mks)
2. the length of the perpendicular from B to AC. (4mks)
3. the length of DC if the area of triangle ADC is equal to 24cm²(3mks)
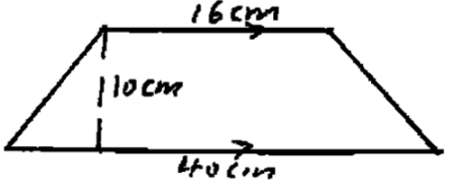
1. Find the area of the following figure. (2mks)
2. A piece of wire is in the shape of an arc of a circle, radius 10.5cm. The angle at the centre is 150°
  1. Calculate the length of the wire. (2mks)
  2. If the wire is bent to form a complete circle, find its radius. (3mks)
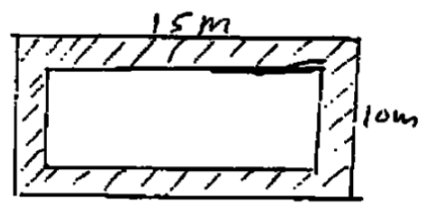
3. A flower garden measuring 10m by 15m is surrounded by a path 2m wide, as shown by the figure below. Find the area of the path. (3mks)
Two business partners Nzau and Masese contributed sh.112,000 and sh 128,000 respectively, to start a business. They agree to share their profits as follows;
30% to be shared equally
30% to be shared in the ratio of their contributions
40% to be retained for the running of the business.
If their total profit for the year 1989 was sh.86400 calculate
1. 1. The amount shared equally. (2marks)
  2. simplified ratio of contribution (2mks)
  3. The amount retained for running the business (2marks)
2. The amount received by each partner. (4 mks)
1. Three litres of water (density 1g/cm³) is added to 12 litres of alcohol (density 0.8g/cm³)
  Calculate:
  1. The mass of water in grammes(g) (2mks)
  2. The mass of alcohol in g. (1mks)
  3. The density of the mixture in g/cm³(2mks)
2. Q right angled triangular prism has length 3m, breadth 2m and height 2.5m. If the mass of the prism is 3.4kg, Calculate.
  1. Area of the cross-section in m² (2 mks)
  2. Volume of the prism in m³(1mk)
  3. The density of the prism in kg/m³(2mks)
1. Express the following decimal as a fraction in its simplest form
  0.185 (2mks)
2. Evaluate the following (3mks)
3. Carol borrowed sh. 150000. She paid back sh.25000 in the first month, sh. 15000 in the second month and sh. 34000 in the third month. She paid the rest in equal amounts for two months. How much did she for each of the last two months?Calculate:
  1. The amount she paid back in the first 3 months. (2mks)
  2. How much did she pay for each of the last two months. (3mks)
Use mathematical tables to evaluate the following
1. 8.457²(2mks)
2. 567.4² (2mks)
3. √456.7 (3mks)
4. √0.7893 (3mks)

MARKING SCHEME

= ¹³/₅ × ¹⁰/₁₇
⁼1⁹/₁₇
let the number of bags be x
Hospital = ¼x
School = ½ × ¾x =³/₈x
Green grocer = ¹/₃ × ³/₈x = ¹/₈x
Total distributed = ¼x + ³/₈x + ¹/₈x = ¾x
¼x − ¹/₈x = 6
¹/₈x = 6
∴ x = 48bags
5a – 4b – 2 [a –(2b + c)]
=5a – 4b – 2a – 4b + 2c
=3a+2c
4 × 4 + 20
−6 × 2 −6
=16+20
−12−6
= 36
−18
=−2
1. 7532
2. Total value = 5 × 100
  = 500
remainder on Thursday = 1948 − 750 = 1198
Remainder on Friday = 1198 − (750+240) =208
No. of oranges sold on Saturday = 208 + 560 = 768
Amount of money on Saturday sales = 768 × 8 = sh.6144
GCD = 2² × 3 = 12
Area = 12 × 12 =144
LCM = 3 × 3 × 5 ×7 = 315min = 5hrs 15min
They last rang at = 11.00p.m − 5h 15min
= 5.45 p.m
Makhoha : Njau : Odhiambo
2 : 3
2 : 5
M:N:O = 4:6:15
Odhiambo contributed = ¹⁵/₂₅ × 120,000
= Sh. 72,000
2t + 3s =390
5t + 2s = 810
4t + 6s =780
15t + 6s = 2430
11t =1650
t = 1650 = sh.150
11
2 × 150 + 3s = 390
3s =90
s =30
∴ 1pair of trousers costs Sh. 150 and 1 shirt Sh. 30
¹/_4x = ⁵/_6x − 7
12x × ¹/_4x = ⁵/_6x × 12x − 7 ×12x
3 = 10 − 84x
84x = 7
x =⁷/₈₄ = ¹/₁₂
0.18 ×4
√(3.24 × 4)
√(3.24 × 4) = 2√3.24
= 2√(³²⁴/₁₀₀)
= 2 × ¹⁸/₁₀ = 2 × 1.8
0.18 ×4 = 0.18 × 4 ×10
√(3.24 × 4) 2 × 1.8 × 10
= 1.8 × 2
18
= 0.182 =0.2
LCM = 2 × 3³ × 5 = 270
n = 270 + 3
1. 3137
2. The no is 4964
3. Difference = 4964 − 3137
  = 1827
No. of hrs = 4 × 24 + (1845 − 0445)
= 96 + 14 =110hrs
Time lost = 110 × 0.5 = 55min
Time = 1845 − 55 = 1750hrs
= 5.50p.m
²/₃ = ¹⁶/₂₄
⁷/₁₂ = ¹⁴/₂₄
⁵/₈ = ¹⁵/₂₄
In ascending order ⁷/₁₂ ,⁵/₈ , ²/₃
1. Area = ½ × 4 × 6
  =12cm²
2. ½ × 10 × h =12
  5h =12
  h = ¹²/₅
  =2.4cm
  ∴ length of perpendicular = 2.4cm
3. ½ × 6 × DC = 24
  3DC = 24
  DC = ²⁴/₃
  = 8cm
1. Area = ½(40 + 16)×10
  =½ × 56 × 10
  = 280cm²
2. 1. L= ¹⁵⁰/₃₆₀ × ²²/₇ × 2 × 10.5
    = 22.5cm
  2. 2πr = 27.5
    2 × ²²/₇ × r = 27.5
    r = 27.5 × 7
    44
    = 4.375
3. Internal dimesions are 11 × 6
  Area of path = (15×10) − (11×6)
  = 150 − 66
  = 84m²
1. 1. Amount = ³⁰/₁₀₀ × 86400
    =Sh. 25,920
  2. Nzau: Masese = 112000:128000
    = 7:8
  3. Amount retained = ⁴⁰/₁₀₀ × 86400
    = Sh. 34560
2. Nzau received = ⁷/₁₅× 25920 + ½ × 25920
  = 12096 + 12960
  = Sh. 25056
  Mases received = ⁸/₁₅ × 25920 + 12960
  = 13824 + 12960
  = Sh. 26784
1. 1. Mass of water = 3000 × 1
    = 3000g
  2. Mass of alcohol = 12000 × 0.8 = 9600g
  3. Density of mixture = 3000+ 9600
    15000
    = 12600
    15000
    = 0.84g/cm³
2. 1. Area of x-section = ½ × 2 × 2.5
    = 2.5m²
  2. vol. of prism = 2.5 × 3 = 7.5m³
  3. density = 3.4
    7.5
    = 0.4533 kg/m³
1. 0.185 = ¹⁸⁵/₁₀₀₀
  = ³⁷/₂₀₀
2. 3½ + 2³/₈ = ⁷/₂ + ¹⁹/₈
  = 28 + 19
  8
  = ⁴⁷/₈
  4¹/₃ − 2⁵/₁₂ = ¹³/₃ − ²⁹/₁₂
  = 52 − 39
  12
  = ²³/₁₂
  ⁴⁷/₈÷ ²³/₁₂ = ⁴⁷/₈× ¹²/₂₃
  = ¹⁴¹/₄₆
  ⁼3³/₄₆
3. 1. Amount paid in 3 months = 25000 + 15000 + 34000
    = Sh.74000
  2. Amount remaining = 150000 − 74000
    = Sh. 76000
    Amount paid last 2 months = 76000
    2
    =Sh. 38000
1. 8.457² = 71.40
  + 12
  71.52
2. 567.4² = (5.647 × 10²)²
  = 5.674² × 10⁴
  = 32.19 × 10⁴
  =321900 or 3.219×10⁵
3. √(456.7) = √(4.567 × 100)
  = 1.37 × 10
  = 13.70
4. √0.7893 = √(^78.93/₁₀₀)
  = 8.843
  10
  = 0.8843