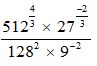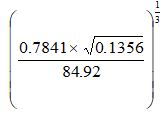Mathematics Questions and Answers - Form 2 Term 1 Opener Exams 2021

1. Given a:b = 2:3 and b:c = 4:8 find a:b:c. (2 marks)
2. Using mathematical tables to find;          (2 marks)
   0.0912³                                                  
3. Solve for x in the equation.          ( 3 marks )
   27^x x 3^(2x-2) = 9 ^{(x +2)} 
4. Simplify:                (4 marks)
   
5. Use logarithms to 4 decimal places to evaluate: (4 marks)
   
6. Use squares, square roots and reciprocals tables only to evaluate;         (4 marks)
        3        +     4     
   √(42.15)      (3.152)² 
7. Find the equation of a line through point (5, −1) and perpendicular to line 4x + 2y – 3 = 0. (4 marks)
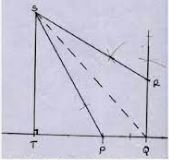
8. Four towns P, Q, R, and S are such that the town Q is 120 Km due to East of town P. Town R is 160km due north of town Q, town S is on a bearing of 330° from Q and on a bearing of 300° from R.
   1. Show the relative position of towns P, Q, R, and S.      (5mks)
      Take the scale of 1cm to rep. 50km.
   2. Use the drawing to determine
      1. The distance SP in Km (2mks)
      2. The bearing of S from P (1mk)

Marking Scheme

1. Given a:b = 2:3 and b:c = 4:8 find a:b:c. (2 marks)
   a:b:c
   (2:3)4
       (4:8)3     m1
   8:12:24
   =2:3:6   A1
2. Using mathematical tables to find;    (2 marks)
   0.0912³ 
   (9.123 x 10⁻²)³
   758.6 x 10⁻⁶
   7.586 x 10⁻⁴
3. Solve for x in the equation.          ( 3 marks )
   27^x x 3^(2x-2) = 9 ^{(x +2)} 
   3^3x x 3 ^{(2x – 2)} = 3 ^{2(x + 2 )}     M1 expressing in index form
   3x + 2x – 2 = 2x + 4             M1 relating index
   3x = 6
   x = 2                      A1 C.A.O
4. Simplify: (4 marks)
   
     M1
     M1
    =¼ × ⁹/₁ = 2¼
5. Use logarithms to 4 decimal places to evaluate: (4 marks)
   
   
    =0.5310
6. Use squares, square roots and reciprocals tables only to evaluate;     (4 marks)
          3       +     4     
   √(42.15)      (3.152)²
   √(42.15)=6.4923
   3.152² = 9.9351
       3      +      4    
   6.4923      9.9351 
   3 x 0.1540 + 4 x 0.1007
   0.462 + 0.4028
   = 0.8648
7. Find the equation of a line through point (5, -1) and perpendicular to line 4x + 2y – 3 = 0. (4 marks)
   4x + 2y = 3
   2y = −4x + 3
   y = −2x + ³/₂
   Gradient (m₁) = −2
   m₁ x m₂ = −1
   −2 x x = −1
           x= −1 = ½
                −2
   (x, y) (5, −1)
   y−−1=½
    x−5
   y + 1 = ½ (x – 5)
   y = ½x−⁵/₂−¹/₁
   y = ½x−3½
8. Four towns P, Q, R, and S are such that the town Q is 120 Km due to East of town P. Town R is 160km due north of town Q, town S is on a bearing of 330° from Q and on a bearing of 300°from R.
   1. Show the relative position of towns P, Q, R, and S.
      Take the scale of 1cm to rep. 50km. (5mks)
      
   2. Use the drawing to determine
      1. The distance SP in Km (2mks)
         4.9 x 50 = 245 Km         M1A1
      2. The bearing of S from P (1mk)
         356°     B1