Mathematics Paper 1 Questions and Answers - Form 4 Opener Term 1 Exams 2022

Share via Whatsapp

Next Topic »
Mathematics Paper 2 Questions and Answers - Form 4 Opener Term 1 Exams 2022

Download PDF for future reference Get on Whatsapp for 50/-

MATHEMATICS
PAPER 1

Instructions to candidates

This paper contains TWO sections: section I and section II
Answer ALL the questions in Section I and only five questions from section II.
Show all the steps in your calculations, giving your answers at each stage in the spaces provided below each question.
Marks may be given for correct working even if the answer is wrong.
Non-programmable silent electronic calculators and KNEC mathematical tables may be used except where stated otherwise.

Questions

SECTION I (50Marks) Answer ALL questions in this section

Evaluate without using tables or a calculator the value of 1.33×0.510.19×0.0017 (3marks)
When a certain number is divided by 48, 72 or 100 the remainder is 3 in each case. Find the number. (3mks)
Find all the integral values of x which satisfy the inequalities (3mks)
20-x>5+2x≥x+5
A Kenyan bank buys and sells foreign currency as shown below.
Buying Selling
Kenya shillings Kenya shillings
1 Euro 84.15 84.26
1 US Dollar 80.12 80.43
A tourist travelling from Britain arrives in Kenya with 5000 Euros. He converts all the Euros to Kenya Shillings at the bank. While in Kenya he spends a total of KSh. 289,850 and then converts the remaining Kenya shillings to US dollars at the bank. Calculate (to nearest dollar) the amount he receives? (3mks)
Complete the figure below so as to make the net of a cuboid. Hence determine the surface area of the cuboid. (4 Marks)
Find the value of x given that is a singular matrix (3 marks)
The figure below shows a solid wedge PQRSTU. Complete the solid showing all the hidden edges with dotted lines. (3marks)
During an annual general meeting at Patel Mixed Day, goats and chicken were slaughtered. The number of heads for both chicken and goats were 45. The total number of legs were 100. Determine the exact number of goats and chicken slaughtered. (3marks)
In a mixed school there are 900 students, out of these 600 are girls.
1. Find the ratio of boys to girls. (2marks)
2. What is the percentage of boys in this school? (1mark)
Find the value of t in the equation (3marks)
t-1 - 4+t =0
3 4
Using tables, find the reciprocal of 0.432 and hence evaluate (3marks)
√0.1225
0.432
Find the equation of the line perpendicular to 3x – 7y – 20 = 0, and passes through the point (5, 2). (3 Marks)
The angle of elevation of the top of a building from a point P is 45°. From another point T, 15 meters nearer the foot of the building, the angle of elevation of the top of the building is 52°. Calculate the height of the building. (3marks)
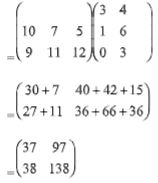
Given A = (10 7 5 9 11 12) and B=( 3 4 1 6 0 3 ), find AB (4mks)
The travel timetable below shows the departure and arrival time for a bus plying between two towns M and R, 300 kilometres apart.
TOWN ARRIVAL DEPARTURE
M 0830h
N 1000h 1020h
P 1310h 1340h
Q 1510h 1520h
R 1600h
Calculate the average speed for the whole journey. (3mks)
Evaluate the value of x in 81^x+1+3^4x=243 (3marks)

SECTION II (50 Marks) Answer only FIVE questions from this section.

A group of choir members decided to raise 3600/= to buy a guitar. Each member was to contribute equal amount. In the preparation process five members transferred to another church which meant the remaining contributors had to pay more to achieve the target.
1. Show that the increase in the contribution per member was:
  Sh. 18,000
  n(n-5)
  if n is the initial number of members. (4 mks)
2. If the increase in the contribution per member was sh. 24, what was the original contribution before the other members left? ( 4 mks)
3. Calculate the percentage increase in the contribution after the others left. (2 mks )
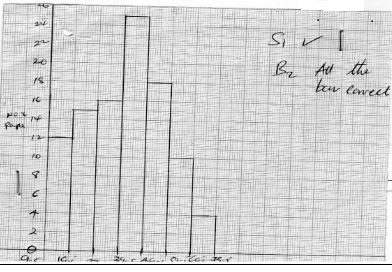
The table below shows the age groups and number of people who are HIV/ AIDS positive in a certain Sub-county in Kenya.

Age group 10-19 20-29 30-39 40-49 50-59 60-69 70-79

No. of people 12 15 16 25 18 10 4
1. State the modal age group. (1mark)
2. Calculate the mean age of the people who are HIV/AIDS Positive. (3marks)
3. Calculate the median of the age group. (3marks)
Using a pair of compass and ruler only construct.
1. Triangle PQR in which PQ =5cm, QPR = 300 and PQR=105°. (3marks)
2. A circle that passes through the vertices of the triangle PQR. Measure its radius. (3marks)
3. The height of triangles PQR with PQ as the base. Measure the height. (2marks)
4. Determine the area of the circle that has outsides the triangle correct to 2 decimal places (2marks)
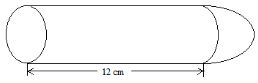
The diagram below shows a solid made of a hemisphere and a cylinder. The radius of both the cylinder and the hemisphere is 3cm. The length of the cylinder is 12cm.
1. 1. Calculate the volume of the solid. (3marks)
  2. The solid fits in a box in the shape of a cuboid 15 cm by 6cmby 6cm. Calculate the volume of the box not occupied by the solid correct to four significant figures. (2marks)
2. 1. Calculate the total surface area of the solid correct to four significant figures. (3marks)
  2. The surface of the solid is to be painted. One millilitre of paint covers an area of 8cm2.The cost of paint is Ksh 900 per litre. Calculate the cost of the paint required. (2marks)
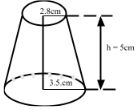
Find
1. The surface area of the frustrum (5 Marks)
2. The volume of frustrum shown. (5 Marks)
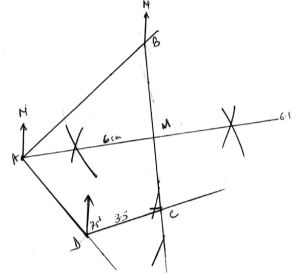
A pirate boat sails from port A on a bearing of 050° at a speed of 112km/h, for 2½ hours to port B. From port B it changes its course and travelled on a bearing of 170° at a speed of 75km/h for 2²/₃ hours toward part C. From C it travelled to port D. D is on a bearing of 130° and 160km from A.
1. Using a scale of 1cm to represent 40km, Draw a diagram showing the positions of the ports A, B, C and D. (4 marks)
2. Use your drawing to find.
  1. The distance CD (1 mark)
  2. The bearing of C from D (1 mark)
3. A marine police patrol leaves port A to intercept the pirate boat at M as it moves from B to C in the shortest time possible.
  1. How far from A will the two boats meet at M? (2 marks)
  2. If the boats meets after 2 hours, what is the speed of the marine police patrol boat? (2 marks)
Helena left town A at 8:00 am and travelled towards town B at an average speed of 64 km/h. half an hour later, Joan left town B and travelled towards A at the same speed if the two towns are 384km apart:
1. At what time of the day did they meet? (5marks)
2. How far from town B was their meeting point? (2marks)
3. How far apart were they at 10:30am (3marks)
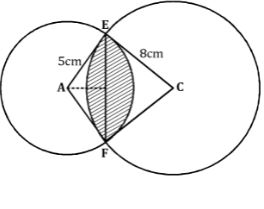
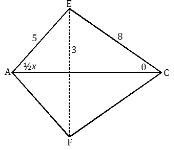
The figure below shows two intersecting circles with centres A and C, of radius 5cm and 8cm respectively. The common chord EF = 6cm

Calculate
1. Angle EAF (2 marks)
2. Angle ECF (2 marks)
3. Calculate the common area between the two intersecting circles. (6 marks)

Marking Scheme

133 X 0.51 X 1000000
0.19 X 0.0017 X 1000000
133 X 51 X 100
19 X 17
2100
2 48 72 100

2 24 36 50

2 12 18 25

2 6 9 25

3 3 9 25

3 1 3 25

5 1 1 25

5 1 1 5

1 1 1

L.C.M = 2⁴ 3² 5²
= 3600
Number =3600 + 3
= 3603
20 – x > 5+2x
15 >3x
x <5
5 + 2x ≥ x + 5
2x – x ≥ 0
3x ≥ 0
x ≥0
5> x ≥ 0
Integral values are 0, 1, 2, 3 and 4
5000 x 84.15 = 420,750
420 750
-289 850
130 900
= 1627.50
≈ 1628
Surface area =
3 x 5 x 2 = 30
2 x 5 x 2 = 20
2 x 3 x 2 = 12
= 62cm²
2x - 1 - x² = 0
x² - 2x + 1 = 0
(x - 1) (x-1) = 0
x = 1
Diagram
G+c=45
4g+2c= 100
G=45-c
4(45 – c) + 2c=100
180 – 4c +2c=100
C=40
g=5
1. boys = 900 – 600= 300
  ratio
  3000:600
  1:2
2. 300/900 x 100
  33¹/₃% M1
4(t-1) – 3(4+t)=0
4t-3t – 4 – 12=0
t- 16 = 0
t= 16
1 = 1x 1
0.432 4.32 x 10^-1
= 0.2375 x 101
= 2.315
= √0.1225 = 2.315x√0.12225
0.432
= 0.35 x 2.315
= 0.81025
7y = 3x – 20
y = x -
g =
Gradient of tar = ∆y/∆x =
= 3y – 6 = -7x + 35
3y = -7x + 41
y = x +
diagram
x = h/tan 52
x = h
tan45 -15
h = h
tan52 tan 45-15
h(1-0.7813) = 15 h =
h = 68.58m
Time taken 1600 h – 830 h = 7hrs 30 min
= 7¹/₂ hrs
Av. speed = 300/7.5
= 40km/h
3^4(x+1) +3^4x = 246
3^4x+4 +3^4x = 246
3^4x(3⁴+1)=246
3^4x=246
81
3^4x=3¹
4x= 1
X=¹/₄
1. Original contribution = ³⁶⁰⁰/_n
  New contribution = ³⁶⁰⁰/_n-5
  Increase = ³⁶⁰⁰/_n-5 = ³⁶⁰⁰/_n
  3600n + 3600n + 18000
  n(n-5)
2. 18000 = 24
  n(n-5)
  18000 = 24n² -120n
  n² – 5n – 750 = 0
  n² – 30n + 25n – 750 = 0
  n (n – 30) + (25 (n – 30 ) = 0
  (n – 30) (n + 25) = 0
  n - 30 = 0
  n + 25 = 0
  but n cannot be –ve n = 30
3. 3600/n= 120 original
  3600/25= 144 new
  increase = ²⁴/₁₀₀ x 100% = 20 % (10 mks)
1. 40 -49
2. x f fx cf
  
  14.5
  24.5
  34.5
  44.5
  54.5
  64.5
  74.5 12
  15
  16
  25
  18
  10
  4 174
  3675
  552
  1112.5
  981
  645
  298 12
  27
  43
  68
  86
  96
  100
  
  Σf=100 Σfx= 4130
  
  x= Σfx/Σf = 4130/100 = 41.30
3. Median = 39.5 + ( ¹⁰⁰/₂ - 43) x 10
  25
  39.5 + 2.8
1. 1. Radius = 3.5 ± 0.1
  2. height construction
    height = 3.4±0.1
2. area of circle outside triangle
  = ²²/₇ x 3.5 – ½ x 3.4 x 5
  = 29.98
1. 1. v=3.142 x 3² x 12+12+²/₃ x 3.142 x 3³
    =339. 336 + 56.556
    = 395.892
    = 395.9
  2. v= 15 x 6 x6 – 395.892
    = 144.108
    =144.1
2. 1. S.A = 3.142 x 3² +2 x3.142 x 3 x 12 + 2 x 3.14 2 x 3²
    = 28 .278 +226.224+56.556
    311.058
    = 311.1
  2. Cost = 311.058 x 900
    8x1000
    = ksh. 34.99
    = 35.0
1. Linear scale factor (L.S.F)
  ^2.8/_3.5 = ⁴/₅
  Area scale factor (A.S.F) ( )2 =
  Volume scale factor (V.S.F)
  (⁴/₅)³ = ⁶⁴/₁₂₅
  From similar triangles
  ^h/_h+5 = ⁴/₅
  5h = 5h + 20
  h = 20cm
  Length of larger cone
  L² = 25² + 3.5² = 625 + 12.25
  =637.25
  L = √637.25
  ∴ l = 25.24
  Curved surface area larger cone
  πrL=²²/₇ x 3.5 x 25.24
  = 277.64cm²Curved S.A of the small cone
  ¹⁶/₂₅ x 277.64 = 99.9cm2
  Total surface area of frustrum
  {22/7 x 2.8 x 2.8} + {22/7 x 3.5 x 3.5} + 99.95 cm²24.64 + 38.5 + 99.95
  = 163.09cm²
2. Volume of small cone
  1/3r2h = 1/3 x 22/7 x 2.8 x 2.8 x 20 = 164.3cm³
  Using volume scale factor (V.S.F)
  Volume of larger cone
  = ¹²⁵/₆₄ x 164.3cm³
  ∴Volume of frustrum|
  ⁶¹/₆₄= x 164.3
  = 156.6cm³
1. Dist. AB = 112 × 5/2 = 280km
  BC = 75 × 8/3 = 200km
  AB = 7cm, BC=5cm, AD=4cm
2. 1. CD = 3.5 × 40 = 140KM
  2. Bearing of C from D is 075°
3. 1. AM = 6 × 40 = 240km
  2. Speed = 240/2
    = 120km/h
1. 64 x 0.5 = 32 km
  384 -32 = 352 km
  Time = Distance
  Relative speed
  = 352
  64 x 2
  = 2.75 hrs
  = 2 hrs 45 min
  meeting time = 8.30 + 2.45
  = 1075
  = 1115 h or 11:15am
2. D = S x T
  = 64 x 2.75
  = 176km
3. At 10:30; time difference = 10.30 – 8.30 = 2 hrs
  64 x 2 x 64 x 2 = 352
  x = 352 – 256 = 96 km apart
Sin 1/2x = 3/5
1/2x = Sin-1 3/5 = 36.87
<EAT = 73.74°
Sin ½θ = 3/8
½θ = Sin-1m(3/8)
<= 22.02
<ECF = 44.05 °

73.74 x 22 x 5² - ¹/₂ x 5 x 5Sin 73.7
360 7
=160.09 - 12
4.09cm

44.05 x 22 x 8² - ¹/₂ x 64Sin44.05
360 7
24.61 - 22.25
2.36
Total area= 4.09 + 2.36
= 6.45cm