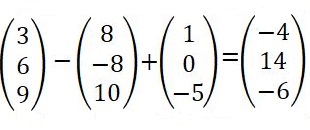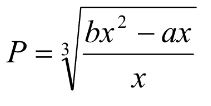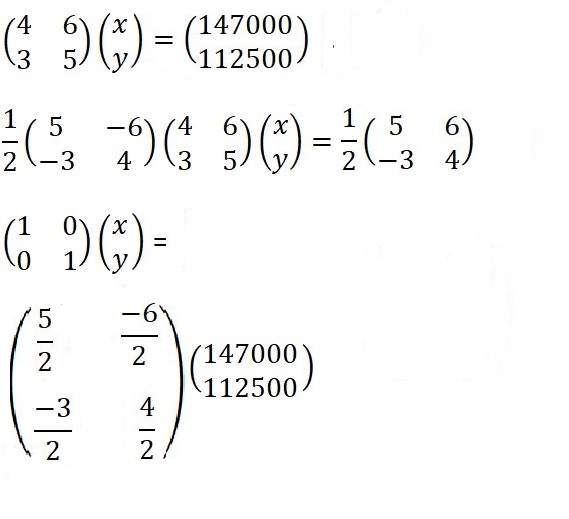Open menu

Mathematics Paper 2 Questions and Answers - Form 4 Opener Term 1 Exams 2022

Share via Whatsapp

« Previous Topic
Mathematics Paper 1 Questions and Answers - Form 4 Opener Term 1 Exams 2022

Next Topic »
English Paper 1 Questions and Answers - Form 4 Opener Term 1 Exams 2022

Download PDF for future reference Get on Whatsapp for 50/-

MATHEMATICS
PAPER 2


Instructions to candidates

  • This paper consists of TWO sections. Section A and Section B.
  • Answer ALL the questions in section A and only FIVE questions from Section B.
  • Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
  • Marks may be given for correct working even if the answer is wrong.
  • Non-programmable silent calculators and KNEC mathematical tables may be used except where stated otherwise.

Questions

  1. Make x the subject of the formula. (3mks)
    MathF4OpT1P2q1
  2. Simplify the following by rationalizing the denominator. (3mks)
        8    
    4-2√3
  3. A quantity P is partly constant and partly varies inversely as square of t. p =6 when t=6 and p=18 when t=3. Find t when p=11. (3mks)
  4. Solve for x in the equation; (3mks)
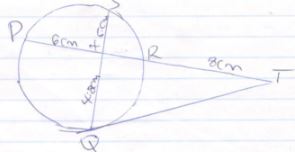
    Log8(x+6) – log8(x-3) = 2/3
  5. In the figure below QT is a tangent to a circle at Q. PXRT and QXS are straight lines. PX =6cm, RT=8cm, Qx=4.8cm and Xs= 5cm.
    MathF4OpT1P2q2
    Find the length of;
    1. XR (2mks)
    2. QT (2mks)
  6. Solve for x and y in the simultaneous equation below. (3mks)
    xy + 6= 0
    x - 2y= 7
  7. Solve for x. (3mks)
    2x2+x-36= 0
  8. Expand (1+2x)7 up to the term in x3, hence use the expansion to estimate the value of (1.02)7 correct to four decimal places. (3mks)
  9. Find the value of y for which MathF4OpT1P2q9 is a singular matrix. (3mks)
  10.              
    1. Find the inverse of the matrix MathF4OpT1P2q10 . (1mk)
    2. Hence solve the simultaneous equation using the matrix method. (3mks)
      4x+3y =6
      3x+5y =5
  11. An item that costs sh. 24, 000 cash can be bought on hire purchase. A customer pays sh.6, 000 as deposit and then makes 6 monthly installments of sh.3, 500 each. Calculate the monthly rate of compound interest, giving your answer to 1 d.p. (3mks)
  12. Barasa shared sh.360, 000 among his children Simiyu, Wasike and Nekesa I the ratio 1:3:5 respectively. How much did each receive? (3mks)
  13. In the arithmetic series 1+4+7+10+…find the sum of the first 100 terms. (3mks)
  14. If  MathF4OpT1P2q14a ,MathF4OpT1P2q14b and MathF4OpT1P2q14c . find 3a-2b+c. (3mks)
  15. Make x the subject (3mks)
    MathF4OpT1P2q15
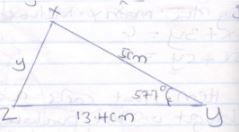
  16. The figure below shows a triangle xyz in which x=13.4cm, z=5cm and ˂xyz= 57.70. Find length y. (3mks)
    MathF4OpT1P2q16

SECTION B: ANSWER 5 QUESTIONS ONLY IN THIS SECTION.

  1.            
    1. Complete the table below for the function y=2x2+3x-5
      x -4 -3 -2 -1 0 1 2
      2x2          0    
      3x -12 18          
      -5 -5     -3     6
      y              
    2. On the grid provided draw the graph of y=2x2+3x-5 for -4≤x≤2. (4mks)
    3. Use your graph to state the roots of
      1. 2x2+3x-5=0 (1mk)
      2. 2x2+6x-2=0 (3mks)
  2. A trader bought 8 cows and 12 goats for a total of ksh.294, 000. If he had bought 1 more cow and 3 more goats he would have spend ksh.337, 500.
    1. Form two equations to represent the above information. (2mks)
    2. Use matrix method to determine the cost of a cow and that of a goat. (3mks)
    3. The trader sold the animals he had bought making a profit of 40% per cow and 45% per goat.
      1. Calculate the total amount of money he received. (3mks)
      2. Determine his profit in Kenyan shillings. (2mks)
  3. The bearing of towns P and Q on a horizontal ground from a tower are 050 and 142 respectively. The angle of elevation of the top of the lower from town P is 34 . Given that P is 200m from the top of the tower and Q is 120m from the base of the tower
    Determine
    1. The height of the tower (3mks)
    2. The angle of elevation of the top of the lower from Q (3mks)
    3. The distance between the two towns P and Q (4mks)
  4. A group of young men decided to raise ksh.480, 000 to start a business. Before actual payment was made four members pulled out and each of the remaining had to pay an additional ksh.20,000 write an expression in terms of p for;
    1.          
      1. Original contribution of each member. (1mk)
      2. Contribution after withdrawal of four members. (1mk)
    2. Form an equation in p and hence determine the number of initial members. (5mks)
    3. Three men Kamau, James and Hassan shared shs.480, 000 such that Kamau: James is 3:2 and James:Hassan is 4:2. Find how much each got. (3mks)
  5. The relationship between two variables S and T is given by the equation S=KTn where K and n are constant
    1. Write down the linear equation relating to S and T (1mk)
    2. Complete the table above for the linear equation relating to S and T(to one decimal place) (2mks)
    3. Draw a suitable straight line graph to represent the data (3mks)
    4. Use your graph to determine the value of K and n (2mks)
    5. Find the value of S when T =3.5 (2mks)
  6.           
    1. The current price of a vehicle is shs 500,000. If the vehicle depreciates at a rate of 15% p.a . Find the number of years it will take for its value to fall to shs 180,000. (4mks)
    2. The cash price of a cooker is shs 9,000. A customer bought the cooker by paying 15 monthly installments of shs 950 each. Calculate:
      1. the carrying charge (3mks)
      2. the rate of interest (3mks)
  7. The table below shows the income tax rates in a certain year.
    Mrs Musau earned a basic salary of ksh 18,600 per month and allowances amounting to ksh.7, 800 per month. She claimed a personal relief of ksh 1,080 per month. Calculate;
    1. Total taxable income in k£ p.a. (2mks)
    2.                
      1. The tax payable in ksh per month without relief. (4mks)
      2. The tax payable in ksh per month after relief. (2mks)
    3. Mrs Musau’s net monthly income. (2mks)
  8. The probability that boys goes to school by bus is 1/3 and by matatu is 1/2. If he uses a bus the probability that he is late to school is 1/5 and if he uses a matatu the probability of being late is 3/10. If he uses other means of transport, the probability of being late is 1/20. What is the probability that
    1. He will be late to school
    2. He will not be late to school
    3. He will be late to school if he does not use a matatu
    4. He neither uses a bus nor matatu but arrives to school early.

Marking Scheme

  1. Make x the subject of the formula. (3mks)
    MathF4OpT1P2q1
    • P2=  x + 2w 
             4x +3R
      P2(4x+3R) = x + 2w
      P24x + P23R = x + 2w
      4P2x-x = 2w - P23R
      x(4P² - 1) = 2w - 3P²R
        4P² - 1         4P² - 1
      x = 2w - 3P²R
              4P²-1

  2. Simplify the following by rationalizing the denominator. (3mks)
        8    
    4-2√3
    •     8      (4 + 2√3)
      4-2√3 (4 + 2√3)  
      8 x 2(2 + √3 )
          16 - 12
      16(2 + √3)
             4
      8(2 + √3)
      16 + 8√3

  3. A quantity P is partly constant and partly varies inversely as square of t. p =6 when t=6 and p=18 when t=3. Find t when p=11. (3mks)
    • p= a + b/t2
      6 = a + b/36
      216 = 36a+b
      216=36a+b
      18=a+b/a
      162= 9a+b
        36 a+b=216
      -4a + b = 162
            27a = 54
      a=2
      9a + b = 162
      18 + b = 162
      b= 162 -18
      b=144
      P= 2 + 144/t2
      11= 2 + 144/t2
      9= 144/t2
      9t² = 144
      9         9
      t=√144/9
      t= 12/3 
      = ±4

  4. Solve for x in the equation; (3mks)
    Log8(x+6) – log8(x-3) = 2/3
    • Log8(x+6) – log8(x-3) = Log88²/₃
      Log8(x+6/x-3) = Log8 4
       x + 6 = 4
         x-3
      x+6 = 4x-12
      18 = 3x
        3     3
      6=x

  5. In the figure below QT is a tangent to a circle at Q. PXRT and QXS are straight lines. PX =6cm, RT=8cm, Qx=4.8cm and Xs= 5cm.
    MathF4OpT1P2q2
    Find the length of;
    1. XR (2mks)
      • 6x = 4.8 x 5
        x= 4.8 x 5
               6
        x=4cm

    2. QT (2mks)
      • QT2 = PT.RT
        QT2= 18.8
        QT2=144
        QT=±12
        +12

  6. Solve for x and y in the simultaneous equation below. (3mks)
    xy + 6= 0
    x - 2y= 7
    • x= 7 + 2y
      y(7 + 2y) + 6 =0
      7y + 2y2 + 6 =0
      2y2 + 7y + 6 =0
      s=2
      p=12
      F=423
      2y2 + 4y + 3y + 6=0
      2y(y+2) +3(y+2) =0
      (2y+3)(y+2)=0
      2y=-3  y=-2
      y= -3/2
      x= 7+2y
      x=7+2(-2)
      x=3
      x=7+2(-3/2)
      x=7+-3
      x=4

  7. Solve for x. (3mks)
    2x2+x-36= 0
    • 2x2+x-36=0
      s=1
      p= -72
      F=9.8
      2x2 + 9x - 8x - 36 = 0
      x(2x+9)-4(2x+9)=0
      (x-4)(2x+9)=0
      x-4 
      2x =-9
      x=-4.5

  8. Expand (1+2x)7 up to the term in x3, hence use the expansion to estimate the value of (1.02)7 correct to four decimal places. (3mks)
    • (1+2x)2
      1  7  21  35  35 
       12  16 15  14  13 
       (2x)°  (2x)  (2x)2 (2x)3   
      1 + 72x + 21.4x2 + 35.8x3
      1 + 14x + 84x2 + 280x3
      1 + 14x + 84x2 + 280x3 + ...
      (1.02)2 →(1 + 0.02)7
      (1 + 2x)7
      2x=0.02
        2    2
      x=0.01
      1 + 14(0.01) + 84(0.01)2 + 280(0.01)3
      1+ 0.14 + 0.0084 + 0.00028
      1.14868

  9. Find the value of y for which MathF4OpT1P2q9 is a singular matrix. (3mks)
    • 18-4y=0
      18=4y
        4   4
      45 =y
  10.              
    1. Find the inverse of the matrix MathF4OpT1P2q10 . (1mk)
      • 20 - 9 = 11
        MathF4OpT1P2qa10a


    2. Hence solve the simultaneous equation using the matrix method. (3mks)
      4x+3y =6
      3x+5y =5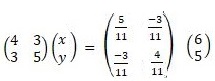
      MathF4OpT1P2qa10b
      x- 30/11 - 15/11 → 15/11
      y= -18/11 x 20/11 → 2/11

  11. An item that costs sh. 24, 000 cash can be bought on hire purchase. A customer pays sh.6, 000 as deposit and then makes 6 monthly installments of sh.3, 500 each. Calculate the monthly rate of compound interest, giving your answer to 1 d.p. (3mks)
    • A = P(1 + r/100)n
      27000 = 24000 (1 + r/100)6
      (1 + r/100)6 = 27000/24000
      n= 6 months
      √(1 + 1/100)6 = 6√1.125
      ≈ 1.02 to 2d.p
      r/100 = 1.02 -1
      r/100 = 0.02
      r= 2%

  12. Barasa shared sh.360, 000 among his children Simiyu, Wasike and Nekesa I the ratio 1:3:5 respectively. How much did each receive? (3mks)
    • 1/9 x 360000 = 40000
      3/9 x 360000 = 120000
      5/9 x 360000= 200000


  13. In the arithmetic series 1+4+7+10+…find the sum of the first 100 terms. (3mks)
    • sn = n/2(2a + (n-1)d)
      s100 = 100/2 ( 2 + 99x3)
      = 14,950

  14. If  MathF4OpT1P2q14a ,MathF4OpT1P2q14b and MathF4OpT1P2q14c . find 3a-2b+c. (3mks)
    •   
      MathF4OpT1P2qa14
  15. Make x the subject (3mks)
    MathF4OpT1P2q15a
    •  P3 = bx² - ax
                    x
       P3 = x(bx - a)
                    x
      P3 = bx - a
      P3 + a = bx 
      P³ + a = x 
           b

  16. The figure below shows a triangle xyz in which x=13.4cm, z=5cm and ˂xyz= 57.70. Find length y. (3mks)
    MathF4OpT1P2q16
    y2 = x2 + 22 - 2 x 2 Cos 57.7°
    y2 = 1342 + 52 - 2 x 134.5 Cos 57.7°
    y2 = 179.56 + 25 - 134Cos 57.7°
    y2= 204.56 - 134 x 0.5344
    y2 = 204.56 - 71.6096
    y2 = √132.9504
    y= ±11.53

SECTION B: ANSWER 5 QUESTIONS ONLY IN THIS SECTION.

  1.            
    1. Complete the table below for the function y=2x2+3x-5
      x -4 -3 -2 -1 0 1 2
      2x2  32  18  8  2  0  2  8
      3x -12 -9  -6  -3  0  3  6
      -5 -5  -5  -5 -5  -5  -5 -5
      y 15   4  -3  -6  -5  0  9
      x=1 or x=2.5

    2. On the grid provided draw the graph of y=2x2+3x-5 for -4≤x≤2. (4mks)
    3. Use your graph to state the roots of
      1. 2x2+3x-5=0 (1mk)
      2. 2x2+6x-2=0 (3mks)
        • y=0  x=1 or x=-2.5
          2x2 + 6x -2 = y
          2x2 + 3x -5=0
          3x + 3=y
          x 0 1 -1
          y 3 6  0

          x=-2 or 1.9
  2. A trader bought 8 cows and 12 goats for a total of ksh.294, 000. If he had bought 1 more cow and 3 more goats he would have spend ksh.337, 500.
    1. Form two equations to represent the above information. (2mks)
      • 8x + 12y = 294000
        9x + 15y= 337500

        4x + 6y = 147000
        3x + 5y = 112500
    2. Use matrix method to determine the cost of a cow and that of a goat. (3mks)
      •       
        MathF4OpT1P2qa20
        367500+ - 337500
        x= 30000
        -220500 + 225000
        y= 4500

    3. The trader sold the animals he had bought making a profit of 40% per cow and 45% per goat.
      1. Calculate the total amount of money he received. (3mks)
        • 40/100 x 30000
          Profit 12000
          45/100 x 4500
          = 2025
          42000 x 8 + 12 x 6525
          336000 + 78300
          = 414300

      2. Determine his profit in Kenyan shillings. (2mks)
        • 414300 - 294000 =120300

  3. The bearing of towns P and Q on a horizontal ground from a tower are 050 and 142 respectively. The angle of elevation of the top of the lower from town P is 34 . Given that P is 200m from the top of the tower and Q is 120m from the base of the tower
    Determine
    1. The height of the tower (3mks)
    2. The angle of elevation of the top of the lower from Q (3mks)
    3. The distance between the two towns P and Q (4mks)
  4. A group of young men decided to raise ksh.480, 000 to start a business. Before actual payment was made four members pulled out and each of the remaining had to pay an additional ksh.20,000 write an expression in terms of p for;
    1.           
      1. Original contribution of each member. (1mk)
        • 480000
             p

      2. Contribution after withdrawal of four members. (1mk)
        • 480000 + 20000
             p -4

    2. Form an equation in p and hence determine the number of initial members. (5mks)
      • 480000 - 480000 = 20000  
             p            p-4
        480000(p-4) - 480000p = 20000(p)(p-4)
        480,000p - 1920000 - 480000p = 20000p2 - 80000p
        -1920000 = 20000p2 - 80000p
        10,000(-192) = 10,000(2p2 - 8p)
        -192 = 2p2 - 8p
        -96 = p2 - 4p
        p2 - 4p + 96 = 0
        4± √(42 - 4x1x - 96)
               2
         4 ±  20
            2
        xd = 24/2 =12

    3. Three men Kamau, James and Hassan shared shs.480, 000 such that Kamau: James is 3:2 and James:Hassan is 4:2. Find how much each got. (3mks)
      • K:J:H
        3:2
           4:2
        6:4:2
        6/12 x 480,000 = 240,000
        4/12 x 480,000 = 160,000
        2/12 x 480,000 = 80,000

  5. The relationship between two variables S and T is given by the equation S=KTn where K and n are constant
    1. Write down the linear equation relating to S and T (1mk)
    2. Complete the table above for the linear equation relating to S and T(to one decimal place) (2mks)
    3. Draw a suitable straight line graph to represent the data (3mks)
    4. Use your graph to determine the value of K and n (2mks)
    5. Find the value of S when T =3.5 (2mks)
  6.           
    1. The current price of a vehicle is shs 500,000. If the vehicle depreciates at a rate of 15% p.a . Find the number of years it will take for its value to fall to shs 180,000. (4mks)
    2. The cash price of a cooker is shs 9,000. A customer bought the cooker by paying 15 monthly installments of shs 950 each. Calculate:
      1. the carrying charge (3mks)
      2. the rate of interest (3mks)
  7. The table below shows the income tax rates in a certain year.
    Mrs Musau earned a basic salary of ksh 18,600 per month and allowances amounting to ksh.7, 800 per month. She claimed a personal relief of ksh 1,080 per month. Calculate;
    1. Total taxable income in k£ p.a. (2mks)
      • 18,600
        +7,800
        26 400
        26400 x 12 = 316800
                 20             20
        £15,840
    2.                
      1. The tax payable in ksh per month without relief. (4mks)
        • 3900 x 2 = 7,800
        • 3900 x 3 = 11,700
        • 3900 x 4 = 15,600
        • 3900 x 5 = 19,500
        • 240 x 7 = 1680
        • 56,280 = 4,690
             12

      2. The tax payable in ksh per month after relief. (2mks)
        • 4690
          1080
          3610

    3. Mrs Musau’s net monthly income. (2mks)
      • 26400
          3610
        22790

  8. The probability that boys goes to school by bus is 1/3 and by matatu is 1/2. If he uses a bus the probability that he is late to school is 1/5 and if he uses a matatu the probability of being late is 3/10. If he uses other means of transport, the probability of being late is 1/20. What is the probability that
    1. He will be late to school
      •    
        MathF4OpT1P2qa24
      • (1/3 x 1/5)+(1/2 x 3/10)+(1/6 x 1/20)
        1/15 + 3/20 + 1/120 
        = 8 +18 + 1
            120
        27/120 = 9/40

    2. He will not be late to school
      • (1/3 x 4/5)+(1/2 x 7/10)+(1/6 x 19/20)=
        4/15 + 7/20 + 19/120 
        = 32 + 42 + 19
             120
        =93/120

    3. He will be late to school if he does not use a matatu
      • (1/3 x 1/5)+(1/6 x 1/20)
        1/15 + 1/120
        8 + 1
        120
        =9/120

    4. He neither uses a bus nor matatu but arrives to school early.
      • 1/6 x 19/20 = 19/20
Join our whatsapp group for latest updates

Download Mathematics Paper 2 Questions and Answers - Form 4 Opener Term 1 Exams 2022.


Tap Here to Download for 50/-


Why download?

  • ✔ To read offline at any time.
  • ✔ To Print at your convenience
  • ✔ Share Easily with Friends / Students

Read 1530 times Last modified on Friday, 11 March 2022 08:26

« Previous Topic
Mathematics Paper 1 Questions and Answers - Form 4 Opener Term 1 Exams 2022

Next Topic »
English Paper 1 Questions and Answers - Form 4 Opener Term 1 Exams 2022

Print PDF for future reference
Published in Form 4 Term 1 Opener Exams 2022 Questions and Answers

Related items

back to top
Get on WhatsApp Download as PDF
.
Subscribe now

access all the content at an affordable rate
or
Buy any individual paper or notes as a pdf via MPESA
and get it sent to you via WhatsApp

 

What does our community say about us?

Join our community on:

  • easyelimu app
  • Telegram
  • facebook page
  • twitter page
  • Pinterest