Physics Paper 1 Questions and Answers - Form 4 Term 2 Opener Exams 2022

Share via Whatsapp

« Previous Topic
Chemistry Paper 3 Questions and Answers - Form 4 Term 2 Opener Exams 2022

Next Topic »
Physics Paper 2 Questions and Answers - Form 4 Term 2 Opener Exams 2022

Download PDF for future reference Get on Whatsapp for 50/-

QUESTIONS

SECTION A: 25 MARKS

The figure below shows part of a vernier callipers when the jaws are closed without an object in between the jaws.
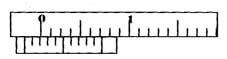
1. State the zero error of the vernier callipers. (1mk)
2. A student used the same vernier calipers to measure the diameter of a test tube of actual diameter 2.15cm. What was the reading shown by the vernier callipers? (2mks)
Xcm³ of substance A of density 800kgm^-3 is mixed with 100cm³ of water of density 1000kgm^-3. The density of the mixture is 960kgm^-3. Determine the value of x. (3mks)
Chalk is denser than air. Explain why chalk dust floats in air. (1 mark)
A bullet of mass 10g travelling at a speed of 400ms^-1 hits a tree trunk, it penetrates the tree trunk and stops inside the trunk after 4 cm.
1. Calculate the average resistance force offered by the trunk to the bullet. (3mks)
2. State the energy changes that takes place. (1mk)
State one way of making surface tension of water stronger. (1mk)
State the law of conservation of energy. (1 mark)
An airtight flask containing a gas is connected to a mercury manometer. The levels of mercury in the two limbs of the manometer are as shown in the diagram below.

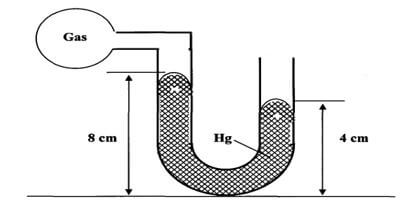
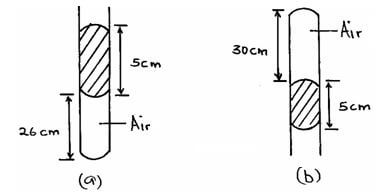
Calculate the pressure of the gas (Density of mercury = 1.36 x 10⁴ kg/m³ and atmospheric pressure = 1.0 x10⁵ N/m²) (3mks)
A column of air 26cm long is trapped by mercury thread 5.0cm long as shown in the figure (a) below. When the tube is inverted as in figure (b) the air column becomes 30cm long. What is the value of atmospheric pressure? (3 marks)
1. State two conditions necessary for a body to be in equilibrium . (2mks)
2. The figure below shows a uniform rod AE which is 40cm long. It has a mass of 2kg and pivoted at D. If 2N is acting at point E, and 30N force is passed through a frictionless pulley
  
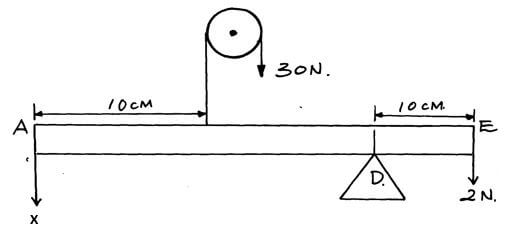
  Find the force X acting at end A (3mks
State the reason why a trailer carrying heavy loads has many wheels. (1 mark)
SECTION B
1. State the Archimedes Principle. (1 mark)
2. The figure below shows rectangular block of height 4cm floating vertically in a beaker containing two immiscible liquid A and B. The densities of the liquid are 8000 kg/m³ and 12,000kg/m³ respectively.
  
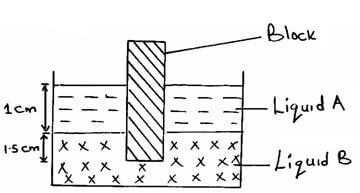
  The cross sectional area is 2cm².Determine.
  1. the weight of the liquid A displaced by the black. (2 marks)
  2. the weight of the liquid B displaced by the block. (2 marks)
  3. the mass of the block. (1 mark)
  4. the density of the block. 2 marks)
1. 1. What is meant by perfectly inelastic collision. (1 mark)
  2. A minibus of mass 1600kg travelling at a constant velocity of 20mls collides with a stationary car of mass 800kg. The impact takes 2 seconds before the two moves together and come to rest after 15 seconds. Determine.
    1. The common velocity. 3marks
    2. The distance moved after the impact. (2 marks)
  3. The impulse force. (3 marks)
1. Sketch a block and tackle pulley system with three movable pulleys in the lower block and two fixed pulleys in the upper block. (2mks)
  Find:
2. 1. Velocity ratio (V.R.) (1mk)
3. A man uses the inclined plane to lift a 50kg load through a vertical line height of 4.0m. The inclined plane makes an angle of 30 with the horizontal. If the efficiency of the inclined plane is 80%, determine.
  1. The effort needed to move the load up the inclined plane at a constant velocity. (3 marks)
  2. The work done against friction in raising the load through the height of 4.0m. (Take g = 10N/kg). (3 marks)
4. The graph below shows the variation of force with distance for a body being towed
  
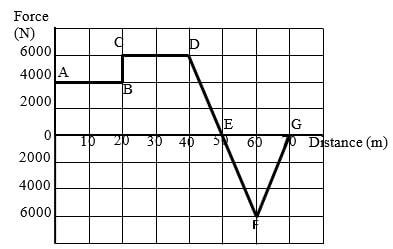
  Calculate the total work done on the body. (3 Marks)
1. The moon goes round the earth at constant speed. Explain why it is true to say that the moon is accelerating. (1 mark)
2. A string of negligible mass has a bucket tied at the end. The string is 60cm long and the buckets has a mass of 45g. The bucket is swung horizontally making 6 revolutions per second. Calculate:
  1. The angular velocity. (1 mark)
  2. The centripetal acceleration. (2 marks)
  3. The tension on the string. (2 marks)
  4. The linear velocity. (1 mark)
3. Figure 6 shows a body of mass;m=200g attached to the centre of a rotating table with a string . The radius of the string was varied and different values of angular velocity recorded. The mass of the body remained constant throughout the experiment.
  
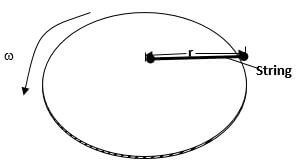
  The results obtained for angular velocity and radius were used to plot the following graph;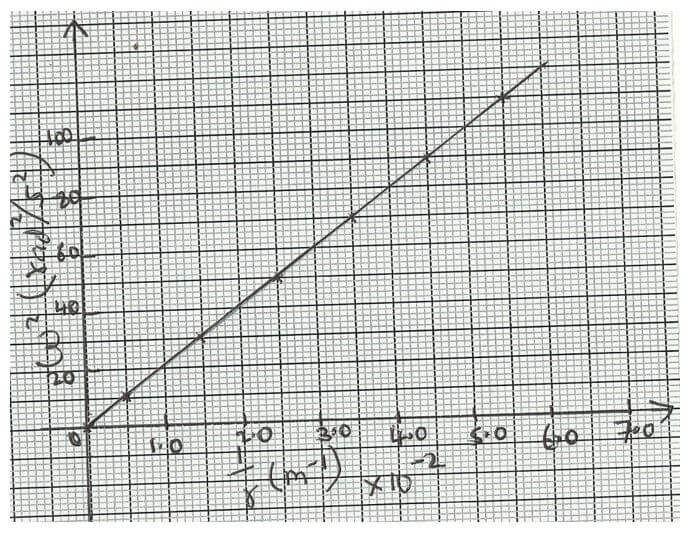
  
  From the above graph;
  1. Calculate the value of the slope. (2mks)
  2. If ω² and 1/r are related by the equation; ω²=p/r×1/m , find the value of P. (2mks)
  3. State the significance of P. (1mk)
1. Define the term specific heat capacity. (1 mark)
2. A block of metal of mass 150g at 100ºC is dropped into a lagged calorimeter of heat capacity 40Jk^-1 containing 100g of water at 25ºC. The temperature of the resulting mixture is 34ºC. (Specific heat capacity of water = 4200Jkgˉ¹).
  Determine;
  1. Heat gained by calorimeter. (2 marks)
  2. Heat gained by water. (2 marks)
  3. Heat lost by the metal block. (1 mark)
  4. Specific heat capacity of the metal block. (3 marks)
3. 200 g of ice at 0°C is added to 400g water in a well lagged calorimeter of mass 40g.The initial temperature of the water was 40°C. If the final temperature of the mixture is X°C,
  (Specific latent of fusion of ice L = 3.36 x 10⁵ Jkg^-1, specific heat capacity of water, c = 4200Jkg-1K^-1, specific heat capacity of copper = 400 Jkg^-1K^-1.)
  1. Derive an expression for the amount of heat gained by ice to melt it and raise its temperature to X°C (2mks)
  2. Determine the value of X. (3mks)

MARKING SCHEME

1. Negative error = 0.06 (-0.06cm)a
2. Reading = 2.15 + 0.06 = 2.21 cm
Total mass = m1 + m²
M1 = 0.8x x m2= 1 x 100
= 0.8xg = 100g
Total = (0.8x + 100)g
Total volume = (x + 100) cm³
Density of mixture = 0.8x + 100 = 0.96
x + 100
x = 4 = 25 cm³
0.16
Due to constant bombardment of chalk and air particles.
1. Work done = F x d = Initial K.E.
  ½ x 10 x (400)² = F x 4
  1000 100
  F = 20000 N
2. K.E. changes to heat and sound.
- Lower the temperature
- Remove impurities
- Energy can neither be created nor destroyed but can be
- Converted/transformed from one form to another.
Gas Pressure = Atmospheric Pressure – Pressure due to Hg Volume
Pg = 1.0x10⁵ – 0.4 x 13600x10
= 94560N/m²
P1V1 = P2V2
26 x (a + 5) = 30(a – 5)
26a + 130 = 30a – 150
4a = 280
a = 70cmHg
1. Sum of clockwise moments must be equal to sum of anticlockwise moments about the same point
  Sum of upward forces must be equal to sum of downward forces
2. sum of clockwise moents = sum of anticlockwise moents
  x(0.3) + 2.0 x 0.1 = (30 x 0.2) + 2 x 0.1
  0.3x = 6.2 – 2.0
  x = 14N
To increase surface area of contact thus reducing pressure exerted on the road
1. Archimedes Principle states that when a body is partially or completely immersed in a fluid it experiences an upthrust which is equal to weight of the fluid displaced.
2. Volume of solid in liquid A = 1cm x 2cm² = 2cm³
  = 2 x 10-6m³
  Mass = volume x density
  = 2 x 10^-6 x 8000
  = 2 x 10^-3 x 8
  = 16 x 10^-3kg
  = 1.6 x 10^-2kg
  W = Mg = 1.6 x 10^-1 = 0.16N
  Volume of the block in liquid B = 1.5cm x 2cm² = 3.0cm³
  = 3 x 10^-6m³
  M = p x V
  = 12000 x 3 x 10^-6
  = 12 x 3 x 10^-3
  = 36 x 10^-3
  = 0.036kg
  W = Mg = 0.036 x 10 = 0.36N
3. Mass of the block =
  Upthrust = 0.36 + 0.16
  = 0.52N = Weight of the block
  W = Mg
  0.52 = M x 10
  M = 0.052kg = 52g
4. Density of the block = mass = 52
  volume 2 x 4
  = 52 = 6.5 g/cm³
  8
1. collision where only linear Momentum is conserved and bodies moves together after collision (coelesce).
2. 1. Momentum before collision = Momentum after collision
    (1600 x 20) + (800 x 0) = (1600 + 800)V
    v = 32000 = 13.33 m/s
    2400
  2. V = U + at
    => 13.33 + 15a => pa = -0.89m/s²
    V² = U² + 2as => s = V² - U² = 0 -(13.33)²
    2a -2 (0.89)
    = 99.83m
  3. Impulse tone = ΔP = 1600(20 - 13.33) for minibus
    T 2
    = 5336N
    Or
    Or 800(13.33 - 0) for a car
    2
    = 5336N
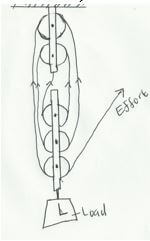
2. V.R =Number of the ropes supporting the load = 6
3. V.R = 1/Sin 20 1/_¹/2 = 2
  M.A = E x V.R
  = 80/100 x 2 = 1.6
  E = L/M.A = 50 x 10 = 312.5N
  1.6
  Work done against friction = Work input – Work output
  Mgh
  Work output = 50 x 10 x 4
  = 2000J
  Work input = Effort x distance moved by effort
  = 312.5 x 4/ sin 30
  = 2500J
  Work done against friction = 2500 – 2000
  = 500J
4. Work = total area under the graph
  = (4000 x 20) + 6000 x 20) + (½ x 6000 x 10) + (½ x 600 x 20)
  = 80000 + 120000 + 30000 + 60000
  = 290,000J
1. The direction is continuously changing.This implies change in velocity hence acceleration.
2. 1. ω=2πf=2×3.142×6=37.704rad/s
  2. a=v²/r=rω²=37.704×37.704×0.6=852.955m/s²
  3. T=Fc=mrω²=0.045×0.6×37.704×37.704=38.38N
  4. V=rω=0.6×37.704=22.62m/s
3. 1. (50-0) =20.0N/Kg
    (2.5-0)
  2. p/m=slope
    p=m×slope=20×0.2=4.0N
  3. It represents centripetal force
1. Specific heat capacity is the quantity of heat required to raise the temp. of a unit mass of a substance by one Kelvin.
2. 1. Heat gained by calorimeter = M_CC_CΔθ
    = Heat capacity x Δθ
    = 40 x (34 – 25)
    = 40 x 9 = 360J
    Heat gained by water = MW x CW x Δθ
    = 0.10 x 4200 x 9
    = 3780J
  2. Heat lost by metal block = 3780 + 360 = 4140J
  3. Heat lost by metal block = Heat gained by calorimeter + water
    Mb x Cb x Δθ = 4140
    0.15 x Cb x (100 – 34) = 4140
    (66 x 0.15)Cb = 4140
    Cb = 4140 = 418.18Jkg^-1k^-1
    66 x 0.15
3. 1. Q= ML + McΔθ
    = 200 x 3.36 x 105 + 200 x 4200 x (x - 0)
    1000 1000
    = 6.72 x 10⁴ + 420X
    67200+420x
  2. Heat lost = heat gained
    67200 + 420x = 67840 – 1696x
    (420 + 1696)x = 67840 – 67200
    2116x = 640
    x = 0.293ºC