- ANSWER ALL THE QUESTIONS IN THE SPACES PROVIDED
- Use logarithms to evaluate : ( 4mks)
34.33
√(5.25 × 0.042) - A sales man gets a commission of 2.5 % on sales upto sh. 100000. He gets an additional commission of 1.6 % on sales above this. Calculate the commission he gets on sales worth sh. 3200000 ( 3mks)
- Make P the subject of the formula ( 3mks)
w = PQ
√(P2 − Q) - Solve the equation 6X2 − 13x + 6 = 0 . Using the completing the square method. (2mks)
- Brian and Bonface working together can do a piece of work in 6 days. Bonface working alone would take 10 days to complete the work. They start working together but after 4 days Bonface leaves and the remaining work is done by Brian. Find how long Brian takes to complete the remaining work. ( 3mks
- Two variables M and N are such that M varies partly as N and Partly as the square root of N. given that N = 16 when M = 500 and N = 25 when M = 800. Find the equation connecting M and N ( 3mks)
- Given log3 = 0.4771 and log 5 = 0.6990, find without using tables or a calculator: log 0.045. (3mks)
- A certain sum of money put to compound interest amounts to sh.5600 at the end of the first year. The interest added at the end of the second year is sh. 672 calculate the rate p.a and the sum invested. (3mks)
- Using compass and ruler only construct a triangle Arc such that AB= 6cm ,BC = 5cm and angle ABC = 67.5ᵒ measure the length of AC ( 4mks)
- Find the constant term in the expansion ( 3mks)
(3x − 1/2x)8 - A tuktuktaxi travelling at 20m/s accelerates uniformly and in 4 seconds, its velocity is 30m/s. it maintains this velocity for another 5 seconds before decelerating uniformly to rest after 3 seconds. calculate the total distance travelled by the tuktuk during the journey. (3mks)
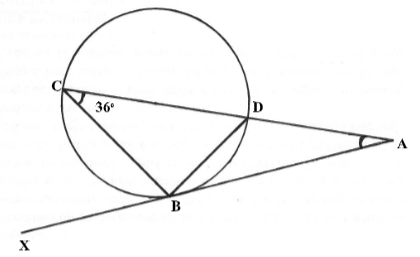
- In the figure below, AB X is a tangent . Angle CAB = 17ᵒ and angle ACB = 36ᵒ calculate the size of angle BDC (3mks)
- Find dy/dx given that y ═ x2 + 4x + 4 ( 3mks)
x + 2 - The perimeter of a triangular field is 120m. two of the sides measures 21m and 40m. calculate the size of the largest angle of the field. (3mks)
- Solve for x: 22x + 3 − 9 (2x) + 1 = 0 ( 3mks)
- Peters joined a firm with a commencing salary of 20,000 per month with an annual increment of 10%. How much did he receive per month during the seventh year. (3mks)
Section B(answer all questions in this section)
- Kamau, Njoroge and Kariuki are practicing archery. The probability for Kamau hitting the target is 2/5 , that of Njoroge hitting the target is ¼ and that of Kariuki hitting the target is 3/7.
Find the probability that in one attempt;- Only one hits the target (2mks)
- All three hit the target (2mks)
- None of them hits the target (2mks)
- Two hit the target (2mks)
- At least one hits the target (2mks)
- Two points P and Q are found on the earth’s surface the position of P is ( 52°S,66°W) and Q ( 52°S,114°E). Taking earth’s radius as 6370km,
- find the difference in longitude between the two points P and Q (1mk)
- calculate the shortestdistance between points P and Q along
- the parallel oflatitutde in km (3mk)
- along the great circle in Km ( 3mks)
- A plane travelling at 800km/hr leaves point P At 10.00am and sais through south pole to point q. Find the local time the plane arrives at point Q to the nearest minute. (3mks)
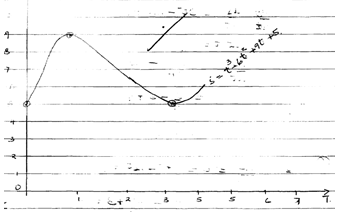
- The distance S meters from a fixed point O, covered by a particle after t seconds B given by the equation S = t3 – 6t2 + 9t + 5
- Calculate the gradient of the curve at t = 0.5 seconds (3mks)
- Determine the values of S at the turning points of the curve ( 3mks)
- Sketch the curve in the space provided. (4mks )
-
- Use trapezium rule with 8 strips to find the area bounded by the curve y = x ² + 2 and the x – axis, x = −2 and x = 2 (5mks)
- Calculate the actual area in (a) above Hence find the percentage error in the area. (5mks)
- A triangle has vertices at A(1,2), B(−2,4) and C(3,5)
- Plot the triangle on the grid provided (1mk)
- Triangle ABC is mapped onto triangle A¹B¹C¹ by a transformation given by M =
State the co-ordinates of triangle A¹B¹C¹ on the same grid plot triangle A¹B¹C¹ (3mks) - Triangle A¹¹B¹¹C¹¹ is the image of triangle A¹B¹C¹ under a reflection on the line y = 0. Plot the triangle A¹¹B¹¹C¹¹ and state its co-ordinates (2mks)
- Triangle A¹¹B¹¹C¹¹ is further rotated through −90° about (0,0) to obtain triangle A¹¹¹B¹¹¹C¹¹¹. Plot the triangle A¹¹¹B¹¹¹C¹¹¹ state its coordinates.(2mks)

MARKING SCHEME
| 1. |  = 73.11
|
M1 M1 M1 A1 |
All logs Addition & sub Division by 2 C.A.O |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. | 2.5 /100 x 100000 = 2,500/=
1.6/100 x 220,000= 3,520/=
Total Comm. = 2,500 + 3520
= 6,020/=
|
M1 M1 A1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3. | W2 = p2 Q2
P2 – Q
W2 = p2 − P2 – Q = W2 Q p2 (W2 − Q) = W2Q
(W2 − Q) W2 – Q
P = ± |
M1 M1 A1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 4. |
P(7 OR >) 21/36 = 7/12 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| 5. | in 1 day ,B+B does 1/6 of the work
in 4 days, they do 1/6 x 4 = 2/3 of the work.
In one day, BOnface does 1/10 of the work
In one day brian does ( 1/6 – 1/10) = 1/15 of the work.
If 1/15 afterwork’s done by brian in 1 day
Then 1/3 will be done in ½ x 1 ÷ 1/15
= 5 days to complete
|
M1 M1 A1 |
Work done by both in 4 days | |||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6. | M = KN + h √N
25k + 5h = 500
16k + 4h = 800
100k+ 20h = 2000
80k + 20h = 4000
20k = - 2000
k = −100
sh = 500 + 2500
sh = 3000
h = 600
∴ M = 600 − 100N
|
B1 M1 A1 B1 |
For two equs
Attempt to solve equations
Boths values for variables correct
Equation connecting m and N
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| 7. | 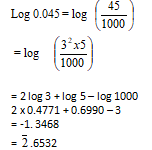 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8. | A = PC ( 1 = r /100)
6272 = 5600 ( 1 = r /100)1
1.12 = 1 = r /100
r /100 = 0.12
r = 12%
P ( 1 = 12 /100)1 = 5600
P = 5600
1.12
P= 5000
|
M1 A1 M1 A1 |
Correct subst. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 9. | 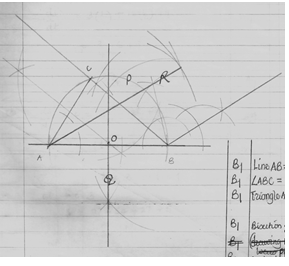 |
4 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 10. | 1 8 28 56 70
(3x)8 (3x)7 (3x)6 (3x)5 (3x)4
1 ( -1/x)1 ( -1/2x)2 ( -1/2x)3 ( -1/2x)4
constan = 70 x 81x4 x 1/16x4
= 354.375 or 2835
8
|
M1 M1 A1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11. |  Distance = area under the curve
= ( ½ x 2 ( 20+30) + 5 x 30 = ½ x 3 x 30) mm
= 100 + 150 + 45
= 295m
|
B1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12. | ∠ ABD = 360° ( angle formed by a tangent in the opp. Segment).
∠ BDA = 127 ( angle in a Δ)
∴∠ BDC = 180 – 127 = 53°
Or ∠ BDC = 17 + 36 ( exterior angel = opp.inter)
|
B1 M1 A1 |
Getting ∠ ABD | |||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | x(x+2) + 2(x+2)
x + 2
= x + 2
dy = 1
dx |
M1 A1 B1 |
Factorization attempt | |||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | 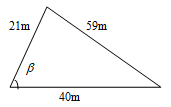 592 = 212 + 402 – 2 x 2 1 x 40 cos β
Cos β = 592 – 212 – 402
–2 x 21 x
= 1440 –1680 = –0.8571 42857
β = 148.9972809°
= 149°
|
M1 M1 A1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15. | 22x+ 3 – 9 (2x) + 1 = 0
Let 2x be y
8y2 – 9y + 1 = 0
Y = 9 ± √81 − 4 × 8
16
= 9 ± 7 = 1 or 1/8
16
2x = 2o = x = 0
Or 2x = 2 -3 = x = −3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16. | 20,000+ 22000+ 24,200 +………..
a = 20,000
r = 22000 = 24200 = 1.1
2000 22000
7th term = 20,000 (1.1)6
= 35,431.20
|
B1 M1 A1 |
For a or r Correct subst. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 17. |
|
10 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 18. |
|
10 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21. | 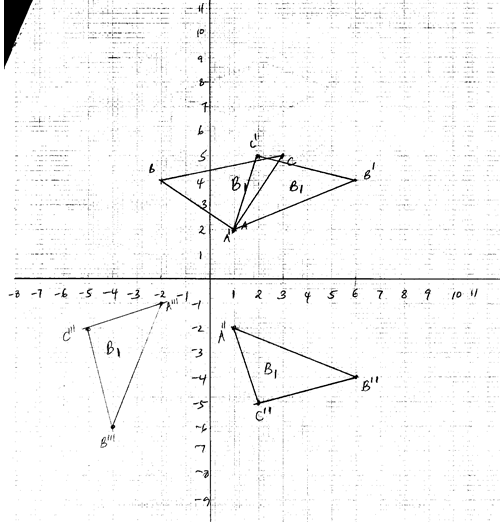 |
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Questions and Answers - Form 4 Mid Term 1 Exams 2023.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students