- Two new dry cells
- An ammeter 0 – 1A
- A voltmeter 0 – 5V
- A resistance wire labelled XY on mm scale
- Jockey or crocodile clip
- Cell holder
- Switch
- Six connecting wires at least three with crocodile clips at one end
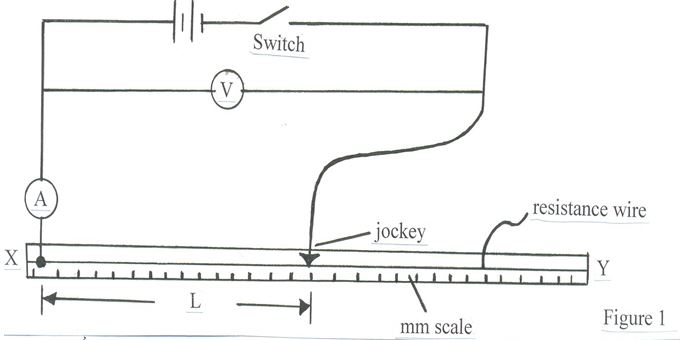
- Set up the circuit as shown in figure 1
- Close the switch and place the jockey in contact with the resistance wire such that the length L, of the wire XY = 0.20m. Measure and record the current, I, through the wire XY and the p.d, V, across it and enter the results in table 1
- Repeat procedure (b) above for the other values of L given. Read and record the corresponding values of I and V.
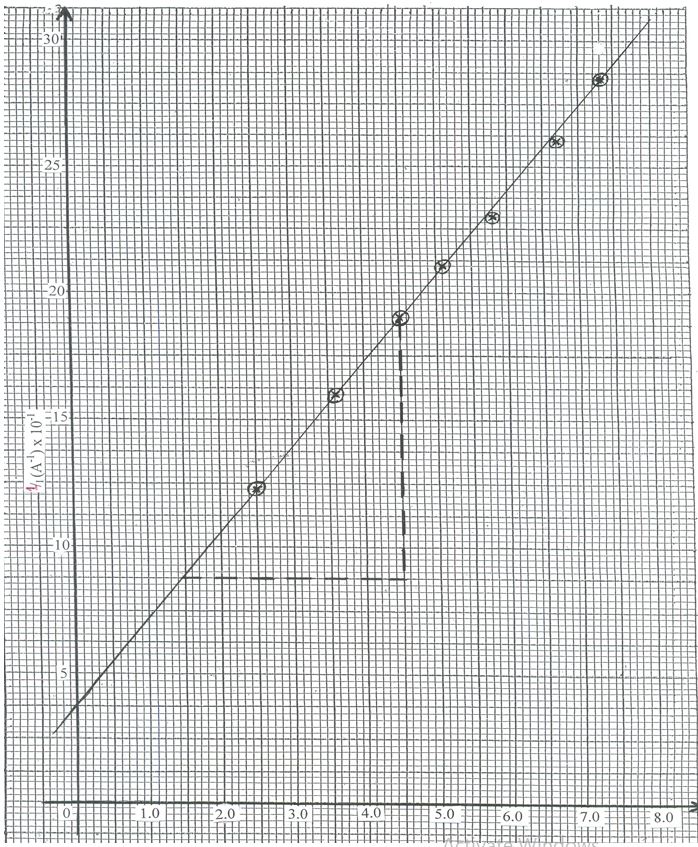
L(cm) 0.2 0.4 0.5 0.6 0.7 0.8 1.0 p.d i (A) R (Ω) I/I(A-1) - Plot a graph of 1/I (y axis) against R (5mks)
- Determine the slope, S, of your graph (3mks)
- Given that I and R of the graph are related by the equation 1/I = R/E + r/E, use your graph to Determine the values of :
E = (3mks)
r = (2mks)
Question two
This question has three parts A, B and C. Answer all the parts
PART A
You are provided with the following:
- A metre rule
- Two identical 100g masses (labeled A and B)
- About 200ml of liquid L in 250ml beaker
- Three pieces of thread, each about half meter long
- Stand with clamps
- Tissue paper.
Proceed as follows:
- Using a stand and one piece of thread, suspend the metre rule in air such that it balances horizontally. Record the position of the centre of gravity. G.
G = ___________________________________________ cm (1mk)
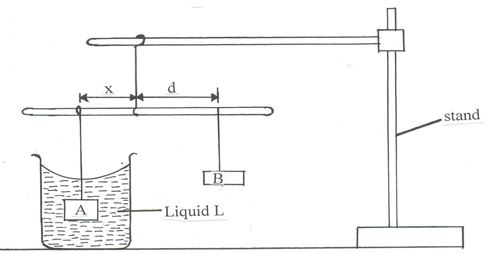
NOTE: The metre rule should remain suspended at this point throughout the experiment. - Set up the apparatus as in figure 2
x d B Liquid L stand Figure 2 A
Suspend the mass A at a distance x = 5cm. adjust the position of mass B until it balances mass A immersed in liquid L. record the distance d, of mass B from the pivot.
Repeat the same process for other values of x in table 2 and complete the table.(3mks)
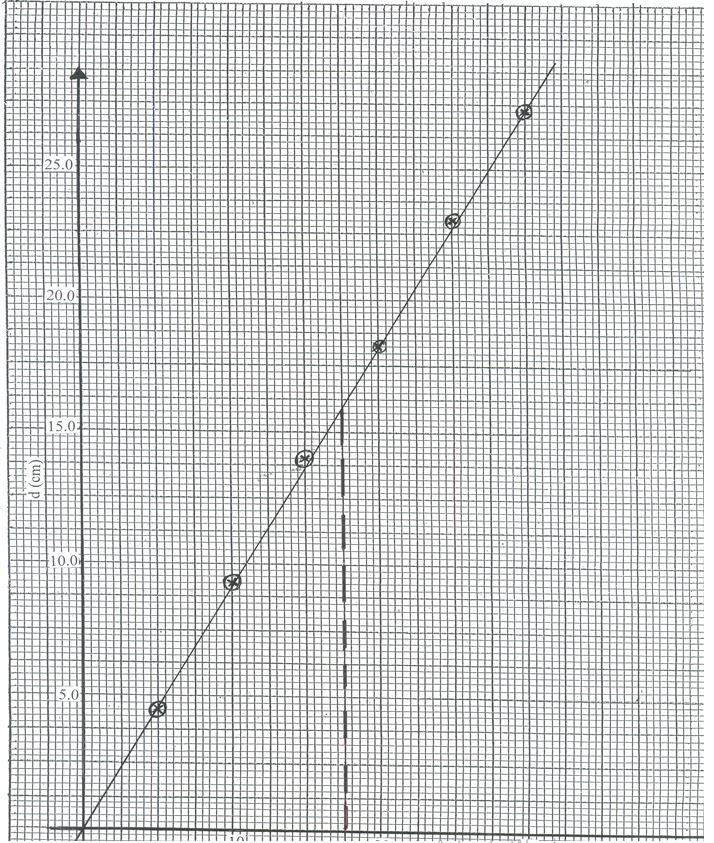
X(cm) 5 10 15 20 25 30 d(cm) - Plot a graph of d (y axis) against x (5mks)
- Determine the slope, S of the graph. (2mks)
- Given S = F,/W where F is the apparent weight of object A in the liquid L and W is the actual weight of A, find:-
- The value of F. (2mks)
- The upthrust, U (2mks)
PART B
You are provided with the following:
- A 70cm long thread
- Stop watch
- Metre rule
- Clamp, boss and retort stand
- Pendulum bob
Proceed as follows:
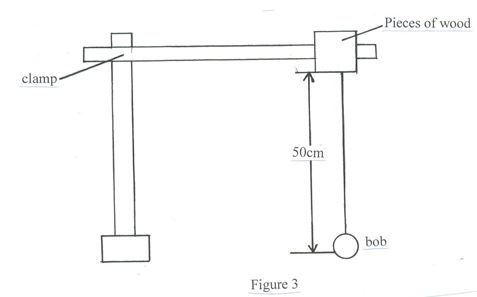
- Using the provided thread, tie the bob to be used as a pendulum. Clamp the thread so that the length of the pendulum to the centre of the bob is 50cm as in figure 3.
Displace the bob slightly so as to oscillate along the vertical plane. Time and record the time, t, for 20 oscillations.
t = ___________________________________________s (1mk)
T = t/20 = _________________________________________ s (1 mk) - If the oscillation of the bob is given by the formula T2 = 4π2L. Use the values in (a) above to determine the value of g. g (1 mk)
PART C
You are provided with the following
- A complete retort stand
- An optical pin
- A concave mirror and a holder or a lump of plasticine
- A cork
- A metre rule
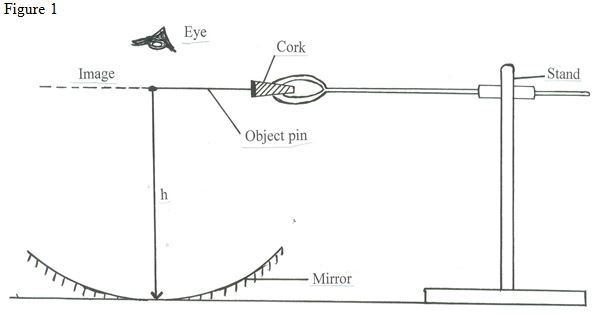
Arrange the apparatus as follows in figure 4
.
- By adjusting the clamp on the stand, move the object pin up and down until the inverted image and object pin appear to coincide (use – no -parallax method). Measure the distance
h = _______________________________________ cm (1mk) - Calculate the value f given that
f = h/2 ______________________________________ cm (1mk)

MARKING SCHEME
QUESTION 1
| L (cm) | 0.2 | 0.4 | 0.5 | 0.6 | 0.7 | 0.9 | 1.0 |
| p.d (V) | 2.05 | 2.25 | 2.35 | 2.40 | 2.45 | 2.50 | 2.55 |
| I (A) | 0.825 | 0.625 | 0.525 | 0.475 | 0.425 | 0.375 | 0.350 |
| R (Ω) | 2.485 | 3.600 | 4.476 | 5.053 | 5.765 | 6.667 | 7.286 |
| 1/1 | 1.212 | 1.600 | 1.905 | 2.105 | 2.353 | 2.667 |
|
P.d (V) – each point ½ mk max 4 points = 2mks
I (A) – each point ½ mk max 4 points = 2mks
R Ω - All points correct = 2mks
1 / I A -1 – all points correct = 1mk
- Axis – labelled with units – 1mk
Scale – uniform and simple and should accommodate all points – 1mk
Plotting – at least 6 points – 2mks
Line – straight with positive gradient passing through 4 correctly plotted points 1mk (5mks) - Slope, S Δ = 1 / I / ΔR
= (19 /4.5– 8.8/1.5) x 10-1 √(1) (intervals)
= 1.02/3.0 √(1) (evaluation)
= 0.34 A -1 Ω-1 √(1) (Accuracy)
∴ S = 0.33 + 0.01
Range (0.32 – 0.34) 3mks - 1/I = 1.R/E + r/E
Y = MX + C √
I/E = slope, S, = 0.34 √
E = I/Slope = 1/0.34 = 2.94√V 3mks
r/E= y – intercept
r = y – intercept x E√
= 3.8 x 10 -1 x 2.94
= 1.117Ω 2mks
Question 2
PART A
- G = 50.0 + 2.0 cm √
Each point ½ mk + 0.1 (3mks)X (cm) 5.0 10.0 15.0 20.0 25.0 30.0 d(cm) 4.5 9.3 14.0
18.4 23.0 27.0
Axis – label with units – 1mk
Scale - uniform and simple
Can accommodate all the points 1mk
Plotting – all points correctly plotted – 2mks
Line – straight, passing through four (4)
Correctly plotted points 1mk (5mks)- Slope S, Δd/Δx = 16/17.5 – 0/0 √= 16/17.5 = 0.9143 (2mks)
- W = 100/1000 x 10 = 1N√
F = SW = 0.9143√ ( 2mks) - U = W – F
= 1 – 0.9143 √
= 0.0857 N √ (2mks)
- W = 100/1000 x 10 = 1N√
Question 2 part A (c)
PART B
- t = 28.53 + 0.02 √1
T = t/20 = 1.4265 √½ - T2 = 4π2L/g√½
g = 4π²x 0.5
(1.4265) 2 √½
= 9.700 √½ (3mks)
NB g = 10 + 1
PART C
- h = 20.0 + 2cm√
- h/2 = 20 /2= 10cm ±1.0√(2mks)
Download Physics Paper 3 Questions and Answers with Confidential - Form 4 End Term 1 Exams 2023.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students