Rotation - Mathematics Form 2 Notes

• Introduction
• Rotational Symmetry of Plane Figures

Introduction

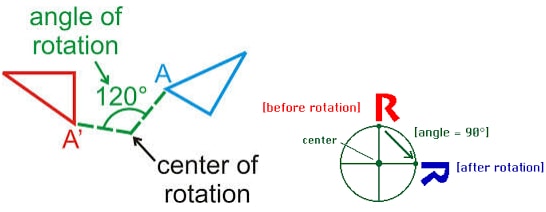
• A transformation in which a plane figure turns around a fixed center point called center of rotation.
• A rotation in the anticlockwise direction is taken to be positive whereas a rotation in the clockwise direction is taken to be negative.
• For example a rotation of 90⁰ clockwise is taken to be negative. − 90⁰ while a rotation of anticlockwise 90⁰ is taken to be +90⁰.

For a rotation to be completely defined the center and the angle of rotation must be stated.

Illustration

• To rotate triangle A through the origin, angle of rotation +¹/₄ turn.
  
  
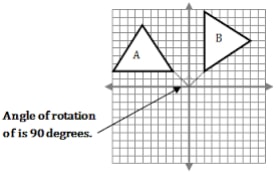
  • Draw a line from each point to the center of rotation ,in this case it’s the origin.
  • Measure 90⁰ from the object using the protacter and make sure the base line of the proctacter is on the same line as the line from the point of the object to the center.
  • The 0 mark should start from the object.
  • Mark 90⁰ and draw a straight line to the center joining the lines at the origin. The distance from the point of the object to the center should be the same distance as the line you drew.This give you the image point
  • The distance between the object point and the image point under rotation should be the same as the center of rotation in this case 90⁰

Illustration.

To find the center of rotation.

• Draw a segment connecting point’s and ′
• Using a compass, find the perpendicular bisector of this line.
• Draw a segment connecting point’s and ′.Find the perpendicular bisector of this segment.
• The point of intersection of the two perpendicular bisectors is the center of rotation. Label this point .

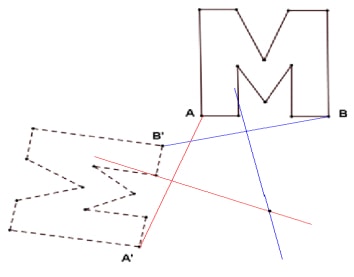
Justify your construction by measuring angles ∠ ′ and ∠ ′. Did you obtain the same measure?

The angle between is the angle of rotation. The zero mark of protector should be on the object to give you the direction of rotation.

Rotational Symmetry of Plane Figures

• The number of times the figure fits onto itself in one complete turn is called the order of rotational symmetry.
  
  Note;
• The order of rotational symmetry of a figure figure = ³⁶⁰/_{angle between two identical parts of the figure}
• Rotational symmetry is also called point symmetry. Rotation preserves length, angles and area, and the object and its image are directly congruent.