Similarity and Enlargement - Mathematics Form 2 Notes

• Introduction
  • Similar Figures
• Enlargement
  • What’s Enlargement?
  • Center of Enlargement
  • Scale Factor
• Congruence Triangles
• Traslation Vector
• Past KCSE Questions on Reflection and Congruence, Rotation, Similarity and Enlargement.

Introduction

Similar Figures

• Two or more figures are said to be similar if:
  • The ratio of the corresponding sides is constant.
  • The corresponding angle are similar

Example 1

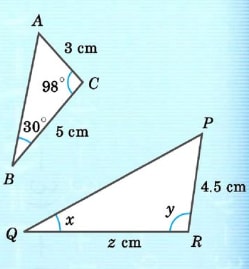
In the figures below, given that △ ABC ~ △ PQR, find the unknowns x, y and z.

Solution

BA corresponds to QP each of them has opposite angle y and 98⁰. Hence y is equal to 98⁰ BC corresponds to QR and AC corresponds to PR.
^BA/_QR=^BC/_QR=^AC/_PR
^AC/_PR=^BC/_QR
³/_4.5=⁵/_z
z= 7.5 cm

Note:

• Two figures can have the ratio of corresponding sides equal but fail to be similar if the corresponding angles are not the same.
  
• Two triangles are similar if either their all their corresponding angles are equal or the ratio of their corresponding sides is constant.

Example:

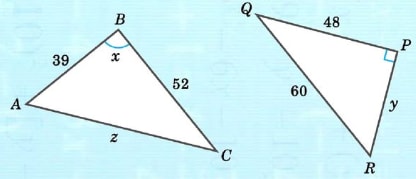
In the figure, △ ABC is similar to △ RPQ. Find the values of the unknowns.

Solution

Since △ ABC~ △ RPQ,

∠B= ∠P
∴x= 90°

Also,
^AB/_RP = ^BC/_PQ
³⁹/_y =⁵²/₄₈
(48 × 39)
     52
∴y = 36
Also,
^AC/_RQ=^BC/_PQ
^z/₆₀=⁵²/₄₈
∴z = 65

Enlargement

What’s Enlargement?

• Enlargement, sometimes called scaling, is a kind of transformation that changes the size of an object.
• The image created is similar to the object. Despite the name enlargement, it includes making objects smaller.
• For every enlargement, a scale factor must be specified. The scale factor is how many times larger than the object the image is.
  Length of side in image = length of side in object × scale factor
  
• For any enlargement, there must be a point called the center of enlargement.
  Distance from center of enlargement to point on image = Distance from Centre of enlargement to point on object X scale factor
  
• The Centre of enlargement can be anywhere, but it has to exist.
  
  
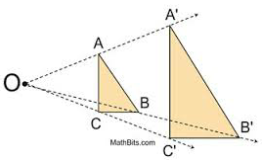
• This process of obtaining triangle A’ B ‘C’ from triangle A B C is called enlargement.
• Triangle ABC is the object and triangles A’ B ‘C ‘Its image under enlargement scale factor 2.
  Hence
  ^OA’/_OA=^OB’/_OB=^OC’/_OC= 2.
• The ratio is called scale factor of enlargement. The scale factor is called liner scale factor
• By measurement OA=1 .5 cm, OB=3 cm and OC =2.9 cm. To get A’, the image of A, we proceed as follows
  OA=1 .5 cm
  ^OA’/_OA=2 (scale factor 2)
  OA’=1.5×2
  =3 cm
  Also ^OB’/_OB=2
  = 3×2
  =6 cm

Note:

• Lines joining object points to their corresponding image points meet at the Centre of enlargement.

Center of Enlargement

• To find center of enlargement join object points to their corresponding image points and extend the lines, where they meet gives you the Centre of enlargement.
• Or Draw straight lines from each point on the image, through its corresponding point on the object, and continuing for a little further.
• The point where all the lines cross is the Centre of enlargement.

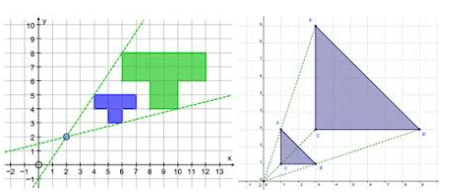
Scale Factor

• The scale factor can be whole number, negative or fraction. Whole number scale factor means that the image is on the same side as the object and it can be larger or the same size,
• Negative scale factor means that the image is on the opposite side of the object and a fraction whole number scale factor means that the image is smaller either on the same side or opposite side.
• Linear scale factor is a ratio in the form a: b or a/b .This ratio describes an enlargement or reduction in one dimension, and can be calculated using.
  
  = New length
     Original length
• Area scale factor is a ratio in the form e: f or e/f. This ratio describes how many times to enlarge. Or reduce the area of two dimensional figure. Area scale factor can be calculated using.
  
  = New Area
     Original Area
  
  Area scale factor= (linear scale factor)²
• Volume scale factor is the ratio that describes how many times to enlarge or reduce the volume of a three dimensional figure. Volume scale factor can be calculated using.
  
  New Volume
  Original Volume
  Volume scale factor = (linear scale factor)³

Congruence Triangles

• When two triangles are congruent, all their corresponding sides and corresponding angles are equal.

Traslation Vector

• Translation vector moves every point of an object by the same amount in the given vector direction.
• It can be simply be defined as the addition of a constant vector to every point.
• Translations and vectors: The translation at the left shows a vector translating the top triangle 4 units to the right and 9 units downward. The notation for such vector movement may be written as: 
  
  
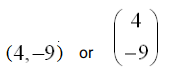
• Vectors such as those used in translations are what is known as free vectors. Any two vectors of the same length and parallel to each other are considered identical. They need not have the same initial and terminal points.

Past KCSE Questions on Reflection and Congruence, Rotation, Similarity and Enlargement.

1. A translation maps a point (1 , 2) onto) (-2, 2). What would be the coordinates of the object whose image is (-3, -3) under the same translation?
2. In the figure below triangle ABO represents a part of a school badge. The badge has as symmetry of order 4 about O. Complete the figures to show the badge.
   
   
3. A point (-5, 4) is mapped onto (-1 , -1 ) by a translation. Find the image of (-4, 5) under the same translation.
4. A triangle is formed by the coordinates A (2, 1 ) B (4, 1 ) and C (1 , 6). It is rotated clockwise through 900 about the origin. Find the coordinates of this image.
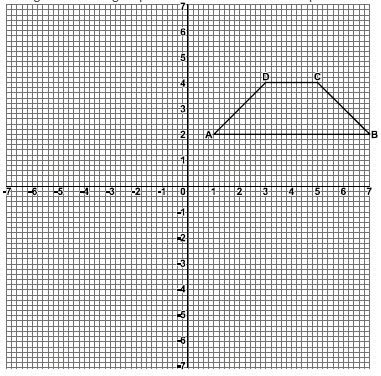
5. The diagram on the grid provided below shows a trapezium ABCD
   
   On the same grid
   1. 1. Draw the image A’B’C’D of ABCD under a rotation of 90⁰ clockwise about the origin .
      2. Draw the image of A”B”C”D” of A’B’C’D’ under a reflection in line y = x. State coordinates of A”B”C”D”
   2. A”B”C”D” is the image of A”B”C”D under the reflection in the line x=0.
      Draw the image A”B” C”D” and state its coordinates.
   3. Describe a single transformation that maps A” B”C”D onto ABCD.
6. A translation maps a point P(3,2) onto P’(5,4)
   1. Determine the translation vector
   2. A point Q’ is the image of the point Q (4, 5) under the same translation. Find the length of ‘P’ Q leaving the answer is surd form.
7. Two points P and Q have coordinates (-2, 3) and (1, 3) respectively. A translation map point P to P’ (10, 10)
   1. Find the coordinates of Q’ the image of Q under the translation
   2. The position vector of P and Q in (a) above are p and q respectively given that mp – nq = 
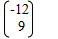
      Find the value of m and n
8. On the Cartesian plane below, triangle PQR has vertices P(2, 3), Q ( 1 ,2) and R ( 4,1 ) while triangles P” q “ R” has vertices P” (-2, 3), Q” ( -1 ,2) and R” ( -4, 1 )
   
   
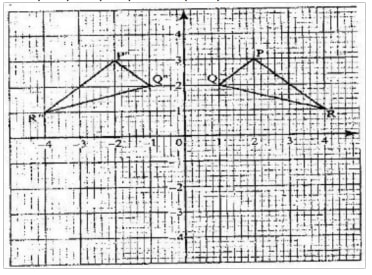
   1. Describe fully a single transformation which maps triangle PQR onto triangle P”Q”R”
      
   2. On the same plane, draw triangle P’Q’R’, the image of triangle PQR, under reflection in line y = -x
   3. Describe fully a single transformation which maps triangle P’Q’R’ onto triangle P”Q”R
      Draw triangle P”Q”R” such that it can be mapped onto triangle PQR by a positive quarter turn about (0, 0)
   4. State all pairs of triangle that are oppositely congruent