Quadratic Expressions and Equations - Mathematics Form 3 Notes

• Perfect Square
• Completing the Square
  • Solutions of Quadratic Equations by Completing the Square Methods
• The Quadratic Formula
• Formation of Quadratic Equations
• Graphs of Quadratic Functions
• Graphical Solutions of Simultaneous Equations
• Past KCSE Questions on the Topic.

---

Perfect Square

• Expressions which can be factorized into two equal factors are called perfect squares.

---

Completing the Square

• Any quadratic expression can be simplified and written in the form ax² x bx + c where a, b and c are constant and a is not equal to zero. We use the expression (^b/₂)² = C to make a perfect square
• We are first going to look for expression where coefficient of x = 1

Example

What must be added to x² + 10x to make it a perfect square?

Solution

• Let the number to be added be a constant c.
• Then x²+ 10x + c is a perfect square.
• Using (^b/₂)²
• (¹⁰/₂)²= c
• c = 25 (25 must be added)

Example

What must be added to x² + _ + 36 to make it a perfect square

Solution

• Let the term to be added be bx where b is a constant
• Then x2+ bx +36 is a perfect square.
• Using ((^b/₂)²= 36
• ^b/₂ =√36
• b/₂ = ±6 b =1 2 x or -1 2 x

We will now consider the situations where a≠ 1 and not equal to zero eg

4x² - 12x + 9 = (2x - 6)²
9x² - 6x + 1 = (3x + 1)²

In the above you will notice that (^b/₂)² = ac . We use this expression to make perfect squares where a is not one and its not zero.

  

Example

What must be added to 25x² + _ + 9 to make it a perfect square?

Solution

• Let the term to be added be bx.
• Then, 25x² + bx + 9 is a perfect square.
• Therefore (^b/₂)²= 25 x 9.
• (^b/₂)² = 225
• ^b/₂ = ±15
• so b = 30 or - 30 The term to be added is thus30 or - 30.

Example

What must be added to _ - 40x + 25 to make it a perfect square?

Solution

• Let the term to be added be ax2
• Then ax2- 40x + 25 is a perfect square.
• Using (^b/₂)²= ac
• (^-40/₂)² = 25a
• 400 = 25a
• a = 16 the term to be added is 16x²

Solutions of Quadratic Equations by Completing the Square Method

Example

Solve x² + 5x+ 1 = 0 by completing the square.

solution

x² + 5x+ 1 = 0 Write original equation.

x² + 5x = -1 Write the left side in the form x² + bx.

x²+ 1 0x + (⁵/₂)²= (⁵/₂)² - 1 Add (⁵/₂)² to both sides

x²+ 10x + ²⁵/₄ = ²¹/₄

(x + ⁵/₂) = ²¹/₄ Take square roots of each side and factorize the left side

x + ⁵/₂ =± √(²¹/4) Solve for x.

= -⁵/₂ ± ^4.583/₂ Simplify

= ^0.417/₂ or ^9.583/₂ Therefore x = - 0.2085 or 4.792

The method of completing the square enables us to solve quadratic equations which cannot be solved by factorization.

Example

Solve 2x² + 4x+ 1 = 0 by completing the square

Solution

2x² + 4x =-1 make coeffiecient of x² one by dividing both sides by 2

x² + 2x = -¹/₂

x² + 2x + 1 = -¹/₂ + 1

Adding 1 to complete the square on the LHS
( x + 1)² = 1
2
x + 1 = ±√¹/₂
x = -1 ± √0.5
= -1 ± 0.7071
x = 0.2929 or - 1.7071

---

The Quadratic Formula

X = -b± √[b²-4ac]
               2a

Example

Using quadratic formula solve 2x2 - 5x - 3 = 0

Solution

Comparing this equation to the general equation ,ax2 + bx + c = 0 we get;a =2 b =-5 c =-5

Substituting in the quadratic formulae

X = -b± √[b²-4ac]
               2a
= -5± √[25 - 4(2)(-3)]
             2(2)
= 5 ± √49
      4
= 5 ±7
     4
= ¹²/₄ or ^-2/₄
X = 3 or ^-1/₂

---

Formation of Quadratic Equations

Peter travels to his uncle’s home, 30 km away from his place. He travels for two thirds of the journey before the bicycle developed mechanical problems an he had to push it for the rest of the journey. If his cycling speed is 10 km\h faster than his walking speed and he completes the journey in 3 hours 30 minutes, determine his cycling speed .

Solution

Let Peters cycling speed be x km/h , then his walking speed is (x - 10) km/h.
Time taken in cycling = (²/₃ of 30) ÷ x
= ²⁰/_x h
Time taken in walking = (30 – 20)÷( x -1 0 )
= ¹⁰/_x-10 h
Total time = (²⁰/_x + ¹⁰/_x-10)h

Therefore (²⁰/_x + ¹⁰/_x-10)) = 3¹/₃
(²⁰/_x + ¹⁰/_x-10)) = ¹⁰/₃
60(x - 10) + 30 (x) = 10(x)(x -10)
10x² – 190x + 600 = 0
x² - 19x + 60 = 0
x =19  ±  √(361-240)
           2
x = 15 or 4
If his cycling speed is 4 km/h , then his walking speed is (4 -1 0 ) km/h, which gives – 6 km/h. Thus, 4 is not a realistic answer to this situation.therefore his cycling speed is 1 5 km/h.

Example

A posite two digit number is such that the product of the digit is 24.When the digits are reversed , the number formed is greater than than the original number by 1 8. Find the number

Solution

Let the ones digit of the number be y and the tens digit be x,
Then , xy = 24…………..1
When the number is reversed, the ones digit is x and the tens digit is y.
Therefore;
(10y + x) – (10x +y) = 1 8
9y- 9x = 1 8
y - x = 2y = x + 2……………..2
Substituting 2 in equation 1 gives;
x(x+2) = 24
x² + 2x - 24 = 0
x =-2  ± √(42-96)
             2
x = 4 or - 6
Since the required number is positive x =4 and y = 4 + 2 =6
Therefore the number is 46

---

Graphs of Quadratic Functions

A quadratic function has the form y = ax² + bx + c where a ≠ 0. The graph of a quadratic function isUshaped and is called a parabola.

For instance, the graphs of y = x² and y = -x²e shown below. The origin (0, 0) is the lowest point on the graph of y = x² and the highest point on the graph of y =-x2 .

The lowest or highest point on the graph of a quadratic function is called the vertex.

The graphs of y = x² and y =-x² are symmetric about the y-axis, called the axis of symmetry.

In general, the axis of symmetry for the graph of a quadratic function is the vertical line through the vertex.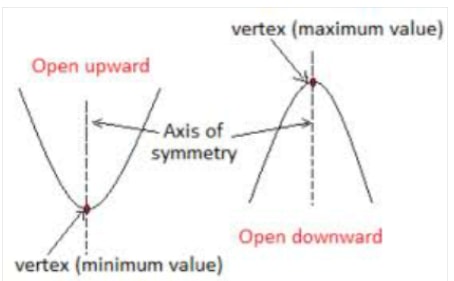


Notes;

The graph of y =x² faces downwards or open upwards and y =-x² faces upwards or open downwards.

Example

Draw the graph of y =-2x² + 5x - 1

Solution

Make a table showing corresponding value of x and y.

X	-1	0	1	2	3
Y	- 8	-1	2	1	-4

Note ; To get the values replace the value of x in the equation to get the corresponding value of x

E.g y = -2(-1)² + 5(-1) - 1 = -8

y = -2(0)² + 5(0) - 1 = -1

Example
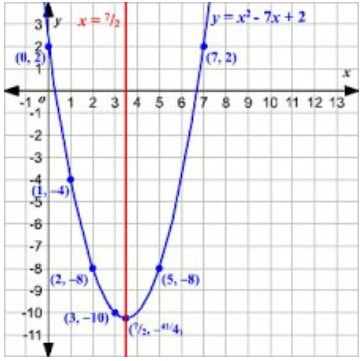
Draw the graph of y = x² - 7x + 2

x	0	1	2	3	5	7
y	2	-4	-8	-1 0	-8	2

---

Graphical Solutions of Simultaneous Equations

We should consider simultaneous equation one of which is linear and the other one is quadratic.

Example

Solve the following simultaneous equations graphically:
y = x² - 2x + 1
y = x² - 2x

Solution

Corresponding values of x and y

x	-2	-1	0	1	2	3	4
y	9	4	1	0	1	4	9

 

x	-2	-1	0	1	2	3	4
y	8	3	0	-1	0	3	8

We use the table to draw the graph as shown below, on the same axis the line y = 5-2x is drawn. Points where the line y =5 - 2x and the curve y = x² - 2x + 1 intersect give the solution. 

The points are (- 2, 9) and (2,1 ).Therefore , when x = -2, y = 9 and when x = 2, y= 1

---

Past KCSE Questions on the Topic.

1. The table shows the height metres of an object thrown vertically upwards varies with the time t seconds. 
   The relationship between s and t is represented by the equations s = at² + bt + 10 where b are constants. 
   

   t	0	1	2	3	4	5	6	7	8	9	1 0
   s		45.1

   1.  
      
      1. Using the information in the table, determine the values of a and b (2 marks)
      2. Complete the table (1 mark)
   2.  
      1. Draw a graph to represent the relationship between s and t (3 marks)
      2. Using the graph determine the velocity of the object when t = 5 seconds
2.  
   
   1. Construct a table of value for the function y = x² – x – 6 for -3≤ x ≤ 4
   2. On the graph paper draw the graph of the function
      Y=x² – x – 6 for -3 ≤ x ≤4
   3. By drawing a suitable line on the same grid estimate the roots of the equation  
      x² + 2x – 2=0
3.  
   
   1. Draw the graph of y= 6 + x - x², taking integral value of x in -4 ≤ x ≤ 5. (The grid is provided. Using the same axes draw the graph of y = 2 – 2x
   2. From your graphs, find the values of X which satisfy the simultaneous equations 
      y = 6 + x - x²
      y = 2 – 2x
   3. Write down and simplify a quadratic equation which is satisfied by the values of x where the two graphs intersect.
4.  
   1. Complete the following table for the equation y = x³ – 5x² + 2x + 9
      

      x	-2	-1.5	-1	0	1	2	3	4	5
      x3		-3.4	-1	0	1		27	64	125
      -5x2	-20	-11.3	-5	0	-5	-20	-45
      2x	-4	-3		0	2	4	6	8	10
      9	9	9	9	9	9	9	9	9	9
      y		-8.7				7		-3

   2. On the grid provided draw the graph of y = x³ – 5x² + 2x + 9 for -2 ≤ x ≤ 5
   3. Using the graph estimate the root of the equation x³ – 5x² + 2 + 9 = 0 between x = 2 and x = 3
   4. Using the same axes draw the graph of y = 4 – 4x and estimate a solution to the equation x² – 5x² + 6x + 5 =0
5.  
   1. Complete the table below, for function y = 2x² + 4x -3
      

      x	-4	-3	-2	-1	0	1	2
      2x2	32		8	2	0	2
      4x - 3			-1 1		-3		5
      y			-3			3	13

   2. On the grid provided, draw the graph of the function y=2x² + 4x -3 for -4 ≤ x ≤ 2 and use the graph to estimate the rots of the equation 2x²+4x – 3 = 0 to 1 decimal place. (2mks)
   3. In order to solve graphically the equation 2x² +x -5 =0, a straight line must be drawn to intersect the curve y = 2x² + 4x – 3. Determine the equation of this straight line, draw the straight line hence obtain the roots. 2x² + x – 5 to 1 decimal place.
6.  
   
   1.  
      
      1. Complete the table below for the function y = x³ + x² – 2x (2mks)
         

         x	-3	-2.5	-2	-1.5	-1	-0.5	0	0.5	1	2	2.5
         x3		15.63				-0.13			1
         x2			4					0.25			6.25
         -2x						1			-2
         y				1.87				0.63			16.88

         
         
      2. On the grid provided, draw the graph of y = x³ + x² – 2x for the values of x in the interval – 3 ≤ x ≤ 2.5
      3. State the range of negative values of x for which y is also negative
   2. Find the coordinates of two points on the curve other than (0, 0) at which x- coordinate and y - coordinate are equal
      
      
7. The table shows some corresponding values of x and y for the curve represented by Y = ¼x³ -2
   

   X	-3	-2	-1	0	1	2	3
   Y	-8.8	-4	-2.3	-2	-1.8	0	4.8

   On the grid provided below, draw the graph of y = ¼x² -2 for -3 ≤ x ≤3. Use the graph to estimate the value of x when y = 2
8. A retailer planned to buy some computers form a wholesaler for a total of Kshs 1 ,800,000. Before the retailer could buy the computers the price per unit was reduced by Kshs 4,000. This reduction in price enabled the retailer to buy five more computers using the same amount of money as originally planned. 
   1. Determine the number of computers the retailer bought
   2. Two of the computers purchased got damaged while in store, the rest were sold and the retailer made a 15% profit Calculate the profit made by the retailer on each computer sold
9. The figure below is a sketch of the graph of the quadratic function y = k (x+1 )(x-2)
   Find the value of k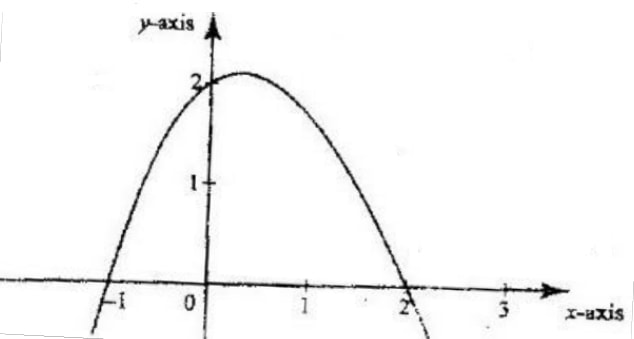
   
   
10.  
    
    1. Draw the graph of y= x² – 2x + 1 for values –2 ≤ x ≤ 4
    2. Use the graph to solve the equations x² – 4= 0 and line y = 2x +5
11.  
    
    1. Draw the graph of y = x³ + x² – 2x for -3≤ x ≤ 3 take scale of 2cm to represent 5 units as the horizontal axis
    2. Use the graph to solve x³ + x² – 6 – 4 = 0 by drawing a suitable linear graph on the same axes.
12. Solve graphically the simultaneous equations 3x–2y =5 and 5x+y=17

Join our whatsapp group for latest updates

---

Download Quadratic Expressions and Equations - Mathematics Form 3 Notes.

Tap Here to Download for 50/-

---

Get on WhatsApp for 50/-

---

Why download?

• ✔ To read offline at any time.
• ✔ To Print at your convenience
• ✔ Share Easily with Friends / Students

---