Trigonometry II - Mathematics Form 3 Notes

• The Unit Circle
• Trigonometric Ratios of Negative Angles
• Use of Calculators
• Radians
• Simple Trigonometric Graphs
  • Graphs of y=sin x
  • Graphs of y=cosx
  • Graph of Tangents
• Solution of Triangles
  • Sine Rule
  • Cosine Rule
• Past KCSE Questions on the Topic.

---

The Unit Circle

 It is circle of unit radius and centre O (0, 0).

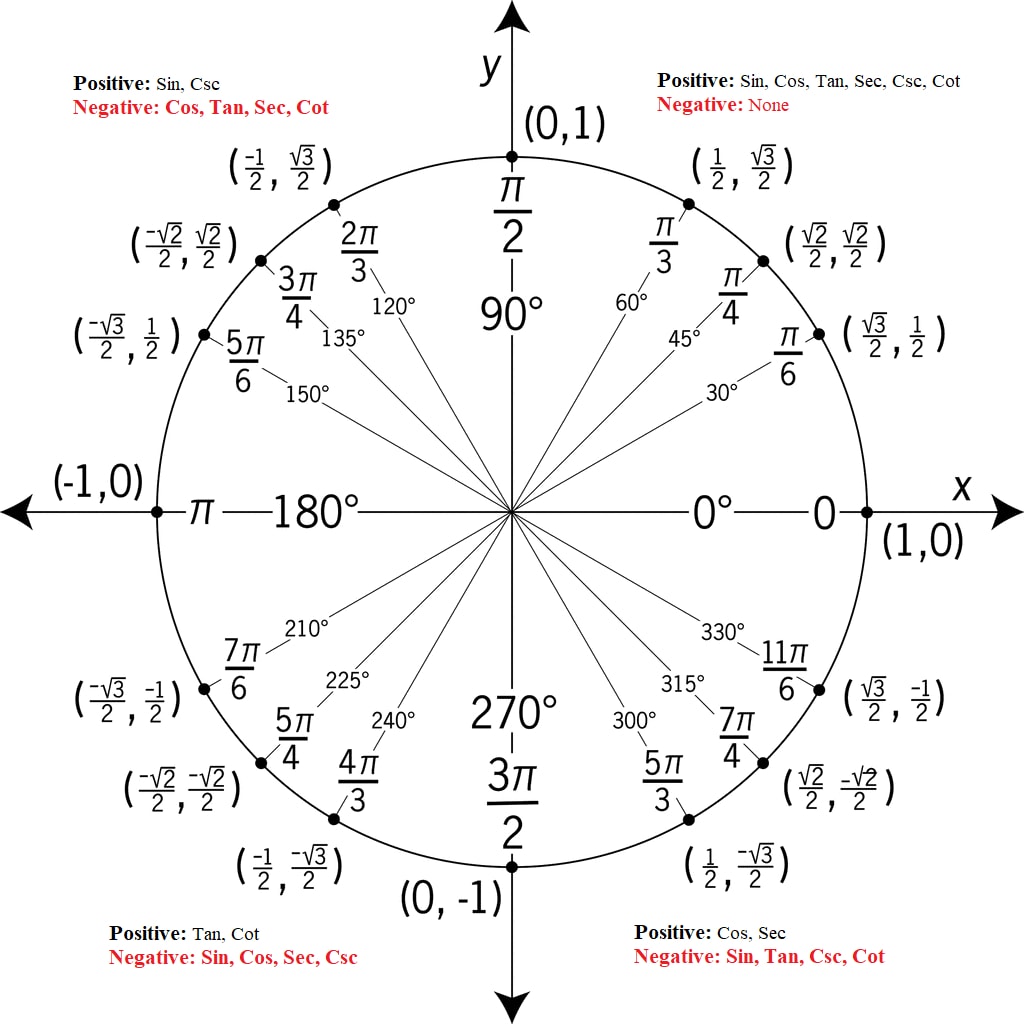
From 0⁰ - 90⁰ is the first quadrant

From 90⁰ - 180⁰ is the second quadrant

From 180⁰ - 270⁰ is the third quadrant

From 270⁰ - 360⁰ is the forth quadrant

An angle measured anticlockwise from positive direction of x – axis is positive. While an angle measured clockwise from negative direction of x – axis is negative.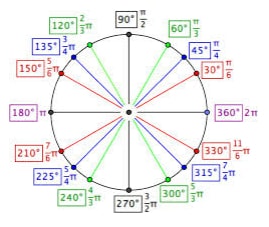

In general, on a unit circle

cos θ⁰ = x co - ordinate of p.
sin θ⁰ = y co - ordinate of p.
tan θ⁰ = y co-ordinate of p. = sinθ
             x co-ordinate of p      cosθ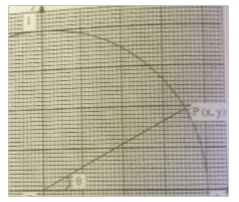

---

Trigonometric Ratios of Negative Angles

In general

1. sin⁡(-0⁰) = - sinθ
2. cos⁡(-0⁰) = cosθ
3. tan (-0⁰) = - tanθ

---

Use of Calculators

Example

Use a calculator to find Tan 30⁰

Solution

• Key in tan
• Key in 30
• Screen displays 0.5773502
• Therefore tan 300 = 0.5774

To find the inverse of sine cosine and tangent

• Key in shift
• Then either sine cosine or tangent
• Key in the number

Note;

Always consult the manual for your calculator. Because calculators work differently

---

Radians

One radian is the measure of an angle subtended at the centre by an arc equal in length to the radius of the circle.

Because the circumference of a circle is 2πr, there are 2π radians in a full circle.

Degree measure and radian measure are therefore related by the equation 360° = 2π radians, or 1 80° = π radians.

The diagram shows equivalent radian and degree measures for special angles from 0° to 360° (0 radians to 2π radians).

You may find it helpful to memorize the equivalent degree and radian measures of special angles in the first quadrant. All other special angles are just multiples of these angles.

Example

Convert 125⁰ into radians

Solution

If 1^c = 360⁰ = 57.29
           2π
Therefore 125⁰= 125 = 2.182 to 4 S.F
                        57.29

Example

Convert the 60⁰ to radians, giving your answer in terms π.

Solution

3600 = 2π^c

Therefore

60⁰ = ( 2π x 60)^c
           360

= (^π/₃)^c

Example

What is the length of the arc that that subtends an angle of 0.6 radians at the centre of a circle of radius 20 cm.

Solution

1^c is subtended by 20 cm
therefore 0.6^c is subtended by 20×0.6 cm = 12 cm

---

Simple Trigonometric Graphs

Graphs of y=sin x

The graphs can be drawn by choosing a suitable value of x and plotting the values of y against the corresponding values of x.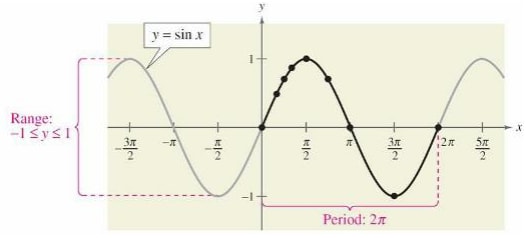

The black portion of the graph represents one period of the function and is called one cycle of the sine curve.

Example

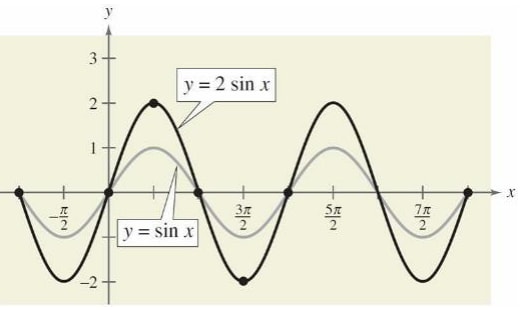
Sketch the graph of y = 2sin x on the interval [–π, 4π].

Solution:

Note that y = 2 sin x = 2

(sin x) indicates that the y-values for the key points will have twice the magnitude of those on the graph of y = sin x.

x	π/2	π	3π	2π
Y=2sin x	2	0	-2	0

To get the values of y substitute the values of x in the equation y =2sin x as follows
y=2 sin (360) because 2 π is equal to 360⁰

Note;

• You can change the radians into degrees to make work simpler.
• By connecting these key points with a smooth curve and extending the curve in both directions over the interval [–π, 4π], you obtain the graph shown in below.
  
  

Graphs of y=cos x

Example

Sketch the graph of y = cos x for 0⁰ ≤ x ≤ 360⁰ using an interval of 30⁰

Solution:

The values of x and the corresponding values of y are given in the table below

x	00	300	600	900	1200	1500	1800	2100	2400	2700	3000	3300	3600
Y=cos x	1	0.8660	0.5	0	-0.5	-0.8660	-1	-0.8660	-0.5	0	0.5	0.8660	1

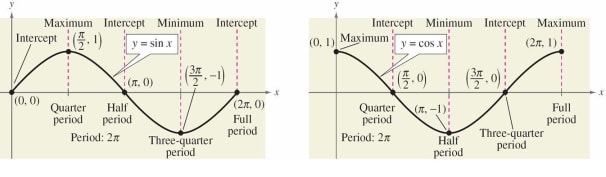
Definition of Amplitude of Sine and Cosine Curves

The amplitude of y = a sin x and y = a cos x represents half the distance between the maximum and minimum values of the function and is given by Amplitude = |a|

 

 

Graph of Tangents

Note;

• As the value of x approaches 90⁰ and 270⁰ tan x becames very large
• Hence the graph of y =tan x approaches the lines x =90⁰ and 270⁰ without touching them.
• Such lines are called asymptotes
  
  

---

Solution of Triangles

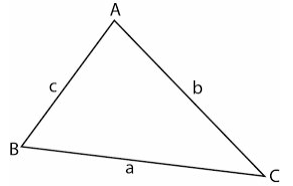
Sine Rule

If a circle of radius R is circumscribed around the triangle ABC ,then ^a/_{sin A} = ^b/_{sin B} = ^c/_{sin C} = 2R.

The sine rule applies to both acute and obtuse –angled triangle.

Example

Solve triangle ABC, given that CAB = 42.90, c= 14.6 cm and a =11 .4 cm

Solution

To solve a triangle means to find the sides and angles not given

^a/_{sin A} = ^c/_{sin C}
^11.4/_{sin 42.9} = ^14.6/_{sin C}

Sin C =14.6 sin42.9 = 0.8720
                 11.4
Therefore C =60.69⁰

Note;

The sine rule is used when we know

• Two sides and a non-included angle of a triangle
• All sides and at least one angle
• All angles and at least one side.

Cosine Rule

a² = b² + c² - 2bccos A OR b² = a² + c² - 2accos B

Example

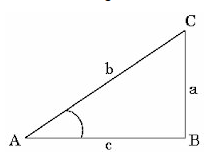
Find AC in the figure below, if AB= 4 cm , BC = 6 cm and ABC =78⁰

Solution

Using the cosine rule

b² + c² - 2 accos B

b² = a² + c² - 2 accos B

b² = 4² + 6² - 2 x 4 x 6cos 780

= 16 + 36 – 48 cos 780
= 52 – 9.979
= 42.02 cm

Note;

The cosine rule is used when we know

• Two sides and an included angle
• All three sides of a triangle

---

Past KCSE Questions on the Topic.

1. Solve the equation
   Sin ^5θ/₂ = -¹/₂ for 0⁰ ≤ θ≤ 180⁰
2. Given that sin θ = 2/3 and is an acute angle find:
   1. Tan θ giving your answer in surd form
   2. Sec²θ
3. Solve the equation 2 sin2(x-30⁰) = cos 60⁰ for – 180⁰ ≤ x ≤ 180⁰
4. Given that sin (x + 30)⁰ = cos 2x⁰ for 0⁰≤ x ≤90⁰ find the value of x. Hence find the value of cos²3x⁰.
5. Given that sin a =¹/_√5 where a is an acute angle find, without using Mathematical tables
   1. Cos a in the form of a√b, where a and b are rational numbers
   2. Tan (90⁰ – a).
6. Give that xo is an angle in the first quadrant such that 8sin²x + 2 cos x -5=0
   Find:
   1. Cos x
   2. tan x
7. Given that Cos 2x⁰ = 0.8070, find x when 0⁰ ≤ x ≤ 360⁰
8. The figure below shows a quadrilateral ABCD in which AB = 8 cm, DC = 12 cm, ∠ BAD = 45⁰, ∠ CBD = 90⁰ and ∠BCD = 30⁰.
   
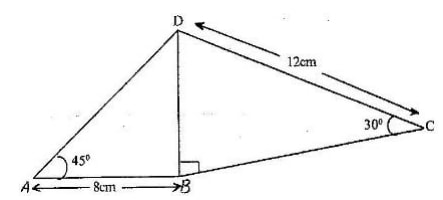
   Find:
   1. The length of BD
   2. The size of the angle ADB
9. The diagram below represents a school gate with double shutters. The shutters are such opened through an angle of 63⁰. The edges of the gate, PQ and RS are each 1.8 m
   
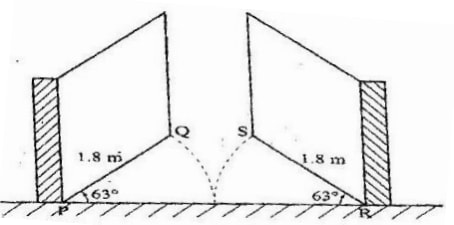
   Calculate the shortest distance QS, correct to 4 significant figures
10. The figure below represents a quadrilateral piece of land ABCD divided into three triangular plots. The lengths BE and CD are 100m and 80m respectively. Angle ABE = 30⁰ ∠ACE = 45⁰ and ∠ACD = 100⁰
    
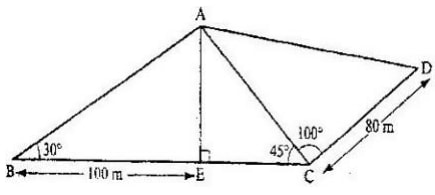
    1. Find to four significant figures:
       The length of AE
       The length of AD
       The perimeter of the piece of land
    2. The plots are to be fenced with five strands of barbed wire leaving an entrance of 2.8 m wide to each plot. The type of barbed wire to be used is sold in rolls of lengths 480m. Calculate the number of rolls of barbed wire that must be bought to complete the fencing of the plots.
11. Given that x is an acute angle and cos x = ^2√5/₅, find without using mathematical5 tables or a calculator, tan (90 – x)⁰.
12. In the figure below ∠A = 62⁰, ∠B = 41⁰, BC = 8.4 cm and CN is the bisector of ∠ACB.
    
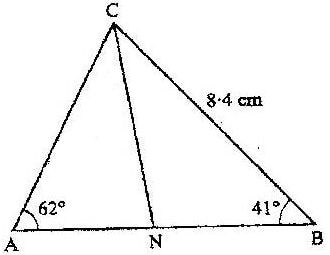
    Calculate the length of CN to 1 decimal place.
13. In the diagram below PA represents an electricity post of height 9.6 m. BB and RC represents two storey buildings of heights 15.4 m and 33.4 m respectively. The angle of depression of A from B is 5.50 While the angle of elevation of C from B is 30.5⁰ and BC = 35m.
    
    
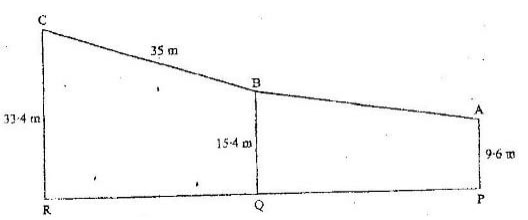
    1. Calculate, to the nearest metre, the distance AB
       
    2. By scale drawing find,
       
       1. The distance AC in metres
       2.  ∠ BCA and hence determine the angle of depression of A from C
          

 

More questions 

1. Solve the equation:
   sin ⁵/₂x = -¹/₂ for 0⁰ ≤ x ≤ 180⁰
2.  
   1. Complete the table below, leaving all your values correct to 2 d.p. for the functions y = cos x and y = 2cos (x + 30)⁰ (2 mks)
      

      X0	00	600	1200	1800	2400	3000	3600	4200	4800	5400
      cos x	1.00			-1.00		0.50
      2cos(x+30)	1.73		-1.73		0.00

   2. For the function y = 2cos(x+30)⁰
      State:
      1. The period (1 mk)
      2. Phase angle (1 mk)
   3. On the same axes draw the waves of the functions y = cos x and y = 2cos(x+30)⁰ for 0⁰ ≤ x ≤ 540⁰. Use the scale 1 cm rep 300 horizontally and 2 cm rep 1 unit vertically (4 mks)
   4. Use your graph above to solve the inequality 2cos(x+30) ≤ cos x (2 mks)
3. Find the value of x in the equation.
   Cos(3x - 180^o) = ^√3/₂ in the range O^o < x < 180^o (3 marks)
4. Given that and tan θ = 11/60 is an acute angle, find without using tables cos (90 –θ)(2mks)
5. Solve for θ if -¼ sin (2x + 30) = 0.1607, 0^o ≤θ ≤360^o (3mks)
6. Given that Cos θ = ⁵/₁₃ and that 270⁰≤θ≤ 360⁰ , work out the value of Tan θ + Sin θ without using a calculator or mathematical tables. (3 marks)
7. Solve for x in the range 0⁰≤ x≤ 180⁰ (4mks)
   -8 sin²x – 2 cos x = -5.
8. If tan x^o = ¹²/₅ and x is a reflex angle, find the value of 5sin x + cos x without using a calculator or mathematical tables
9. Find θ given that 2 cos 3θ -1 = 0 for 0^o ≤ θ≤ 360o
10. Without a mathematical table or a calculator, simplify: Cos300^ox Sin120^o  
    giving your answer in rationalized surd form.                Cos330^o – Sin 405^o
11. Express in surds form and rationalize the denominator.
                     1                   
    Sin 60^oSin 45^o - Sin 45^o
12. Simplify the following without using tables;
    Tan 45 + cos 45sin 60

Join our whatsapp group for latest updates

---

Download Trigonometry II - Mathematics Form 3 Notes.

Tap Here to Download for 50/-

---

Get on WhatsApp for 50/-

---

Why download?

• ✔ To read offline at any time.
• ✔ To Print at your convenience
• ✔ Share Easily with Friends / Students

---