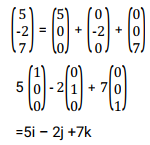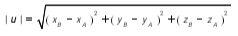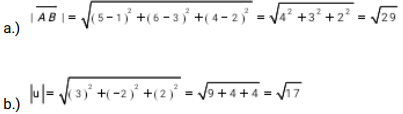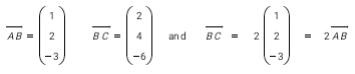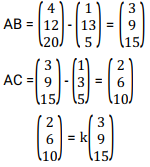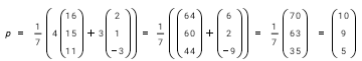- Vectors in 3 Dimensions
- Column and Position Vectors
- Magnitude of a 3 Dimensional Vector.
- Distance Formula for a 3 Dimensional Vector
- Parallel Vectors and Collinearity
- Proportional Division of a Line
- The Ratio Theorem
- Past KCSE Questions on the Topic

Vectors in 3 Dimensions
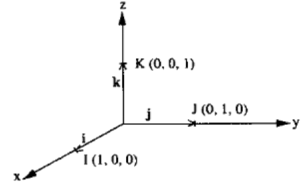
- 3 dimensional vectors can be represented on a set of 3 axes at right angles to each other (orthogonal), as shown in the diagram.
- Note that the z axis is the vertical axis.
- To get from A to B you would move:
4 units in the x-direction, (x-component)
3 units in the y-direction, (y-component)
2 units in the z-direction. (z-component)
In component form:
- In general:



Column and Position Vectors
- In three dimensions, a displacement is represented b a column vector of the form
where p,q and r are the changes in x,y,z directions respectively.
Example
The displacement from A (3, 1, 4 ) to B ( 7 ,2,6) is represented b the column vector,
The position vector of A written as OA is where O is the origin
Addition of vectors in three dimensions is done in the same way as that in two dimensions.
Example
Column Vectors in Terms of Unit Vectors
In three dimension the unit vector in the x axis direction is = ![]() ,that in the dirction of the y axis is =
,that in the dirction of the y axis is = while that in the direction of z – axis is =
Diagrammatic Representation of the Vectors.
Three unit vectors are written as;
Example
Express vector in terms of the unit vector i, j and k
Solution
Note;
- The column vector
can be expressed as ai + bj + ck

Magnitude of a 3 Dimensional Vector.
- Given the vector AB = xi + yj + 2k,then the magnitude of AB is written as |AB| = √(x2 +y2 +z2)
- This is the length of the vector.
- Use Pythagoras’ Theorem in 3 dimensions.
AB2 = AR2 + BR2
= (AP2 + PR2) + BR2
=(xB − xA)2 + (yB − yA)2 + (zB − zA)2
→
and if u = AB then the magnitude of u, |u| = length of AB

Distance Formula for a 3 Dimensionsional Vector
- Recall that since: =
, then
if then |u| = √(x2 +y2 +z2)
- Since x = xB − xA and y = yB −yA and zB − zA

Example:
- If A is (1, 3, 2) and B is (5, 6, 4)
→
Find |AB| - If
. Find |u|
Solution

Parallel Vectors and Collinearity
Parallel Vectors
- Two vectors are parallel if one is scalar multiple of the other.i.e vector a is a scalar multiple of b ,i.e. a =kb then the two vectors are parallel.
Note;
- Scalar multiplication is simply multiplication of a regular number by an entry in the vector
Multiplying by a Scalar
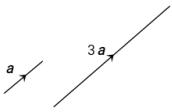
- A vector can be multiplied by a number (scalar).e.g. multiply a by 3 is written as 3a.
- Vector 3a has three times the length but is in the same direction as a .In column form, each component will be multiplied by 3.
- We can also take a common factor out of a vector in component form. If a vector is a scalar multiple of another vector, then the two vectors are parallel, and differ only in magnitude. This is a useful test to see if lines are parallel.
Example
if 
Collinear Points
Points are collinear if one straight line passes through all the points. For three points A, B, C - if the line AB is parallel to BC, since B is common to both lines, A, B and C are collinear.
Test for collinearity
Example
A is (0, 1, 2), B is (1, 3, –1 ) and C is (3, 7, –7) Show that A, B and C are collinear.
Solution
→ →
AB and BC are scalar multiples, so AB is parallel to BC. Since B is a common point, then A, B and C are collinear.
In general the test of collinearity of three points consists of two parts
- Showing that the column vectors between any two of the points are parallel
- Showing that they have a point in common.
Example
A (0,3), B (1 ,5) and C ( 4,1 1 ) are three given points. Show that they are collinear.
Solution
AB and BC are parallel if AB = kBC, where k is a scalar
Therefore AB//BC and point B (1, 5) is common. Therefore A,B,and C are collinear.
Example
Show that the points A (1, 3, 5) ,B(4, 12, 20) and C are collinear.
Solution
Consider vectors AB and AC
Hence k =2/3
AC =2/3 AB
Therefore AB//AC and the two vectors share a common point A.The three points are thus collinear.
Example
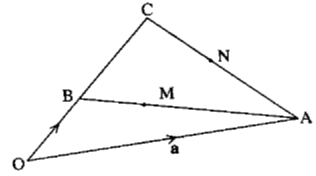
In the figure above OA = a OB = b and OC = 3OB
- Express AB and AC in terms of a and b
- Given that AM = ¾ AB and AN = ½ AC, Express OM and O in terms of a and b
- Hence ,show that OM and N are collinear
Solution
- AB = OA + OB
= − a + b
AC = − a + 3b - OM =OA + AM
= OA + ¾AB
= a +¾(− a + b)
= a − ¾a +¾b
= ¼a + ¾b
ON =OA +AN
=OA + ½AC
a + ½(− a + 3b)
a = a − ½a + 3/2b
= ½ a + 3/2b - OM = kON ¾ b + ¼a = k/2a + 3k/2b
Comparing the coefficients of a;
1/4 = k/2
k = 1/2
Thus, OM = 1/2 ON.
Thus two vectors also share a common point ,O .Hence, the points are collinear.

Proportional Division of a Line
Internal Division
- In the figure below, the line is divided into 7 equal parts
- The point R lies 4/7 of the ways along PQ if we take the direction from P to Q to be positive, we say R divides PQ internally in the ratio 4 : 3.
- If Q to P is taken as positive,then R divides QP internally in the ratio 3 : 4 .Hence, QR : RP = 3 : 4 or, 4 QR = 3RP.
External Division
- In internal division we look at the point within a given interval while in external division we look at points outside a given interval,
- In the figure below point P is produced on AB
- The line AB is divided into three equal parts with BP equal to two of these parts. If the direction from A to B is taken as positive, then the direction from P to B is negative.
- Thus AP : PB = 5 : -2.In this case we say that P divides AB externally in the ratio 5 : −2 or P divides AB in the ratio 5 : −2.
Points, Ratios and Lines
Finding the ratio in which a point divides a line.
Example:
The points A(2, –3, 4), B(8, 3, 1) and C(12, 7, –1 ) form a straight line. Find the ratio in which B divides AC.
Solution
B divides AC in ratio of 3 : 2
Points Dividing Lines in Given Ratios.
Example:
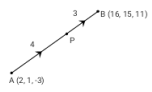
P divides AB in the ratio 4:3. If A is (2, 1, –3) and B is (16, 15, 11 ), find the co-ordinates of P.
Solution:
→ → →
AP = 4 so 3AP = 4PB
→ 3
PB
3(p – a) = 4(b – p)
3p – 3a = 4b – 4p
7p = 4b + 3a
p = 1/7(4b + 3a)
Points Dividing Lines in Given Ratios Externally.
Example:
Q divides MN externally in the ratio of 3:2. M is (–3, –2, –1 ) and N is (0, –5, 2).Find the co-ordinates of Q.
Note that QN is shown as –2 because the two line segments are MQ and QN, and QN is in the opposite direction to MQ.


The Ratio Theorem
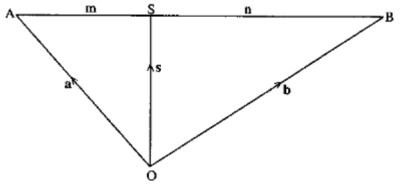
The figure below shows a point S which divides a line AB in the ratio m : n
Taking any point O as origin, we can express s in terms of a and b the positon vectors of a and b respectively.
OS = OA + AS
But AS = m AB
m+n
Therefore, OS = OA + m AB
m+n
Thus S = a + m (−a + b)
m+n
= a − m a + m b
m+n m+n
= (1 − m )a + m b
m+n m+n
= (m+n−m)a + m b
m+n m+n
= n a + m b
m+n m+n
This is called the ratio theorem. The theorem states that the position vectors s of a point which divides a line AB in the ratio m: n is given by the formula;
S = n a + m b
m+n m+n
where a and b are positon vectors of A and B respectively. Note that the sum ofco-ordinates n/m+n and m/m+m= 1
Thus ,in the above example if the ratio m : n = 5 : 3
Then m = 5 and n = 3
OR = 3 a + 3 b
5+3 5+3
Thus, r = 3/8a + 3/8b
Example
A point R divides a line QR externally in the ratio 7 : 3. If q and r are position vectors of point Q and R respectively, find the position vector of p in terms of q and r.
Solution
We take any point O as the origin and join it to the points Q, R and P as shown below
QP: PR = 7: −3
Substituting m = 7 and n = −3 in the general formulae;
OP = −3 q + 7 r
7+(−3) 7+(−3)
P = −3/4 q + 7/4r
Vectors can be used to determine the ratio in which a point divides two lines if they intersect
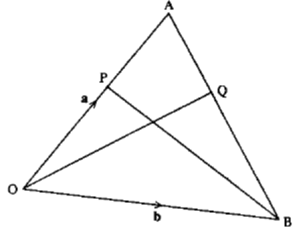
Example
In the below OA = a and OB = b. A point P divides OAin the ratio 3:1 and another point O divides AB in the ratio 2 : 5. If OQ meets BP at M
Determine:
- OM : MQ
- BM : MP
Let OM : MQ = k : (1 – k) and BM –MP = n : ( 1 – n)
Using the ratio theorem
OQ = 5/7 a + 2/7 b
OM= kOQ
= k(5/7 a+ 2/7 b)
Also by ratio theorem;
OM = nOP +( 1 – n )OB
But OP = 3/4 a
Therefore, OM = n (3/4 a) + (1−n)b
Equating the two expressions;
k(5/7 a+ 2/7 b) = n (3/4a) + ( 1−n )b
Comparing the co-efficients
5/7 k = 3/4n………..1
2/7k = 1 − n……..2
k = 21/25 and n = 10/13
The ratio BM :MP = 10/13 : 3/13
= 10: 3

Past KCSE Questions on the Topic
- The figure below is a right pyramid with a rectangular base ABCD and VO as the height. The vectors AD= a, AB = b and DV = v

- Express
- AV in terms of a and c
- BV in terms of a, b and c
- M is point on OV such that OM: MV=3:4, Express BM in terms of a, b and c. Simplify your answer as far as possible
- Express
- In triangle OAB, OA = a, OB = b and P lies on AB such that AP: BP = 3.5
- Find the terms of a and b the vectors
- AB
- AP
- BP
- OP
- Point Q is on OP such AQ = −5/8a + 9/40b
Find the ratio OQ: QP
- Find the terms of a and b the vectors
- The figure below shows triangle OAB in which M divides OA in the ratio 2: 3 and N divides OB in the ratio 4:1 AN and BM intersect at X

- Given that OA = a and OB = b, express in terms of a and b:
- AN
- BM
- If AX = sAN and BX = tBM, where s and t are constants, write two expressions for OX in terms of a, b, s and t
Find the value of s
Hence write OX in terms of a and b
- Given that OA = a and OB = b, express in terms of a and b:
- The position vectors for points P and Q are 4i + 3j and 6j + 6 k respectively. Express vector PQ in terms of unit vectors i, j and k. Hence find the length of PQ, leaving your answer in simplified surd form.
- In the figure below, vector OP = p and OR =r. Vector OS = 2r and OQ = 3/2p.

- Express in terms of p and r (i) QR and (ii) PS
- The lines QR and PS intersect at K such that QK = mQR and PK = nPS, where m and n are scalars. Find two distinct expressions for OK in terms of p,r,m and n. Hence find the values of m and n.
- State the ratio PK: KS
- Point T is the midpoint of a straight line AB. Given the position vectors of A and T are i−j + k and 2i+1½ k respectively, find the position vector of B in terms of i, j and k
- A point R divides a line PQ internally in the ration 3:4. Another point S, divides the line PR externally in the ration 5:2. Given that PQ = 8 cm, calculate the length of RS, correct to 2 decimal places.
- The points P, Q, R and S have position vectors 2p, 3p, r and 3r respectively, relative to an origin O. A point T divides PS internally in the ratio 1:6
- Find, in the simplest form, the vectors OT and QT in terms p and r
- Show that the points Q, T, and R lie on a straight line
- Determine the ratio in which T divides QR
- Two points P and Q have coordinates (-2, 3) and (1 , 3) respectively. A translation map point P to P’ (10, 10)
- Find the coordinates of Q’ the image of Q under the translation
- The position vector of P and Q in (a) above are p and q respectively given that mp – nq =
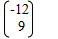
Find the value of m and n
- Given that qi + 1/3j + 2/3 k is a unit vector, find q
- In the diagram below, the coordinates of points A and B are (1, 6) and (15, 6) respectively). Point N is on OB such that 3 ON = 2 OB. Line OA is produced to L such that OL = 3 OA

- Find vector LN
- Given that a point M is on LN such that LM: MN = 3: 4, find the coordinates of M
- If line OM is produced to T such that OM: MT = 6:1
- Find the position vector of T
- Show that points L, T and B are collinear
- In the figure below, OQ = q and OR = r. Point X divides OQ in the ratio 1:2 and Y divides OR in the ratio 3:4 lines XR and YQ intersect at E.

- Express in terms of q and r
- XR
- YQ
- If XE = mXR and YE = nYQ, express OE in terms of:
- r, q and m
- r, q and n
- Using the results in (b) above, find the values of m and n.
- Express in terms of q and r
- Vector q has a magnitude of 7 and is parallel to vector p. Given that p= 3i – j + 1½ k, express vector q in terms of i, j, and k.
- In the figure below, OA = 3i + 3j ABD OB = 8i – j. C is a point on AB such that AC:CB 3:2, and D is a point such that OB//CD and 2OB = CD (T17)

Determine the vector DA in terms of I and j - In the figure below, KLMN is a trapezium in which KL is parallel to NM and KL = 3NM

Given that KN = w, NM = u and ML = v. Show that 2u = v + w - The points P, Q and R lie on a straight line. The position vectors of P and R are 2i + 3j + 13k and 5i – 3j + 4k respectively; Q divides SR internally in the ratio 2: 1 . Find the
- Position vector of Q
- Distance of Q from the origin
- Co-ordinates of points O, P, Q and R are (0, 0), (3, 4), (11 , 6) and (8, 2) respectively. A point T is such that the vector OT, QP and QR satisfy the vector equation OT = QP + ½QT. Find the coordinates of T.
- In the figure below OA = a, OB = b, AB = BC and OB: BD = 3:1

- Determine
- AB in terms of a and b
- CD, in terms of a and b
- If CD: DE = 1:k and OA: AE = 1:m determine
- DE in terms of a, b and k
- The values of k and m
- Determine
- The figure below shows a grid of equally spaced parallel lines

AB = a and BC = b- Express
- AC in terms of a and b
- AD in terms of a and b
- Using triangle BEP, express BP in terms of a and b
- PR produced meets BA produced at X and PR = 1/9b – 8/3a
By writing PX as kPR and BX as hBA and using the triangle BPX determine the ratio PR: RX
- Express
- The position vectors of points x and y are x = 2i + j – 3k and y = 3i + 2j – 2k respectively. Find XY 2. Given that X = 2i + j− 2K, y = -3i + 4j – k and z= 5i + 3j + 2k and that p= 3x – y + 2z, find the magnitude of vector p to 3 significant figures.
Download Vectors II - Mathematics Form 3 Notes.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students