- Introduction
- Forming Linear Inequalities
- Solution by Graphing
- Optimization
- Past KCSE Questions on the Topic.

Introduction
- Linear programming is the process of taking various linear inequalities relating to some situation, and finding the "best" value obtainable under those conditions.
- A typical example would be taking the limitations of materials and labor, and then determining the "best" production levels for maximal profits under those conditions.
- In "real life", linear programming is part of a very important area of mathematics called "optimization techniques".
- This field of study are used every day in the organization and allocation of resources.
- These "real life" systems can have dozens or hundreds of variables, or more. In algebra, though, you'll only work with the simple (and graph able) two-variable linear case.
- The general process for solving linear-programming exercises is to graph the inequalities (called the "constraints") to form a walled-off area on the x,y-plane (called the "feasibility region").
- Then you figure out the coordinates of the corners of this feasibility region (that is, you find the intersection points of the various pairs of lines), and test these corner points in the formula (called the "optimization equation") for which you're trying to find the highest or lowest value.
Example
Suppose a factory want to produce two types of hand calculators, type A and type B. The cost, the labor time and the profit for every calculator is summarized in the following table:
| Type | Cost | Labor Time | Profit |
| A | Sh 30 | 1 hour | Sh 10 |
| B | Sh 20 | 4 hours | Sh 8 |
Suppose the available money and labors are ksh 1 8000 and 1 600 hours. What should the production schedule be to ensure maximum profit?
Solution
Suppose x1 is the number of type A hand calculators and x2 is the number of type B hand calculators and y to be the cost. Then, we want to maximize p = 10x1 + 8x2 subject to
30x+20y ≤18000
x+4y≤1600
x≥0, y≥0
where p is the total profit.

Forming Linear Inequalities
In linear programing we are going to form inequalities representing given conditions involving real life situation.
Example
Esha is five years younger than his sister. The sum of their age is less than 36 years. If Esha’s age is x years, form all the inequalities in x for this situation.
Solution
The age of Esha’s sister is x +5 years.
Therefore, the sum of their age is;
x + (x + 5) years
Thus;
2x +5 < 36
2x < 31
X > 15.5
X > 0 ( age is always positive)

Solution by Graphing
Solutions to inequalities formed to represent given conditions can be determined by graphing the inequalities and then reading off the appropriate values ( possible values)
Example
A student wishes to purchase not less than 1 0 items comprising books and pens only. A book costs sh.20 and a pen sh.1 0.if the student has sh.220 to spend, form all possible inequalities from the given conditions and graph them clearly, indicating the possible solutions.
Solution
Let the number of books be x and the number of pens then, the inequalities are;
- x + y ≥ 10 ( the items bought to be atlest ten)
- x + y ≤ 220 (only sh.220 is available)
This simplifies to 2x + y ≤ 22 - x > and y > 0( number of items bought cannot be negative).
The graph below represents the inequalities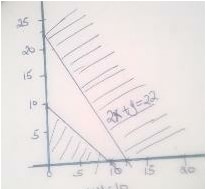
All the points in the unshaded region represent possible solutions. A point with co-ordinates ( x ,y) represents x books and y pens. For example, the point (3, 1 0 ) means 3 books and 1 0 pens could be bought by the students.

Optimization
- The determination of the minimum or the maximum value of the objective function ax + by is known as optimization.
- Objective function is an equation to be minimized or maximized
Example
A contractor intends to transport 1 000 bags of cement using a lorry and a pick up. The lorry can carry a maximum of 80 bags while a pick up can carry a maximum of 20 bags. The pick up must make more than twice the number of trips the lorry makes and the total number of trip to be less than 30.The cost per trip for the lorry is ksh 2000, per bag and ksh 900 for the pick up.Find the minimum expenditure.
Solution
If we let x and y be the number of trips made by the lorry and the pick up respectively. Then the conditions are given by the following inequalities;
- x + y < 30
- 80x + 20y ≥ 1000, which simplifies as 4x + y ≥ 50
- y > 2x
- x < 0
The total cost of transporting the cement is given by sh 2000x + 900y.This is called the objective function.
The graph below shows the inequalities.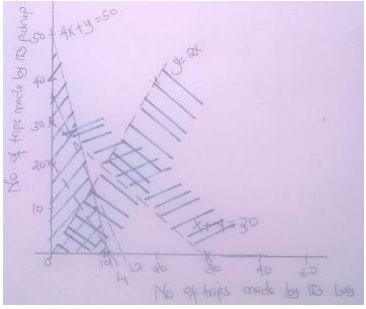
From the graph we can identify 7 possibilities
(7,22),(8,18),(8,19),(8,20),(8,21),(9,19),(9,20)
Note;
Co-ordinates stands for the number of trips. For example (7, 22) means 7 trips by the lorry and 22 trips by the pickup. Therefore the possible amount of money in shillings to be spent by the contractor can be calculated as follows.
- (2000×7) + ( 900 ×22) = 33800
- (2000×8) + ( 900 ×18) = 32200
- (2000×8) + ( 900 ×19) = 33100
- (2000×8) + ( 900 ×20) = 34000
- (2000×8) + ( 900 ×21) = 34900
- (2000×9) + ( 900 ×19) = 35100
- (2000×9) + ( 900 ×20) = 36000
We note that from the calculation that the least amount the contractor would spend is sh.32200.This is when the lorry makes 8 trips and the pick- up 1 8 trips. When possibilities are many the method of determining the solution by calculation becomestedious.
The alternative method involves drawing the graph of the function we wish to maximize or minimize, the objective function. This function is usually of the form ax +by , where a and b ar constants.
For this ,we use the graph above which is a convenient point (x , y) to give the value of x preferably close to the region of the possibilities. For example the point ( 5, 1 0) was chosen to give an initial value of thus ,2000x + 900y = 1 9000.we now draw the line 2000x + 900y=1 9000.such a line is referred to us a
search line.
Using a ruler and a set square, slide the set square keeping one edge parallel to l1 until the edge strikes the feasible point nearest 1 ( see the dotted line l2) From the graph this point is (8,1 8), which gives the minimum expenditure as we have seen earlier.The feasible point furthest from the line l1 gives the
maximum value of the objective function.
The determination of the minimum or the maximum value of the objective function ax + by is known as optimization.
Note;
The process of solving linear equations are as follows
- Forming the inequalities satisfying given conditions
- Formulating the objective function .
- Graphing the inequalities
- Optimizing the objective function
This whole process is called linear programming.
Example
A company produces gadgets which come in two colors: red and blue. The red gadgets are made of steel and sell for ksh 30 each. The blue gadgets are made of wood and sell for ksh 50 each. A unit of the red gadget requires 1 kilogram of steel, and 3 hours of labor to process. A unit of the blue gadget, on the other hand, requires 2 board meters of wood and 2 hours of labor to manufacture. There are 180 hours of labor, 120 board meters of wood, and 50 kilograms of steel available. How many units of the red and blue gadgets must the company produce (and sell) if it wants to maximize revenue?
Solution
The Graphical Approach
Step 1 . Define all decision variables.
Let: x1 = number of red gadgets to produce (and sell)
x2 = number of blue gadgets to produce (and sell)
Step 2. Define the objective function.
Maximize R = 30x1 + 50x2 (total revenue in ksh)
Step 3. Define all constraints.
- x1 ≤50 (steel supply constraint in kilograms)
- 2x2 ≤120 (wood supply constraint in board meters)
- 3x1 + 2x2 ≤1 80 (labor supply constraint in man hours)
- x1, x2≥0 (non-negativity requirement)
Step 4. Graph all constraints.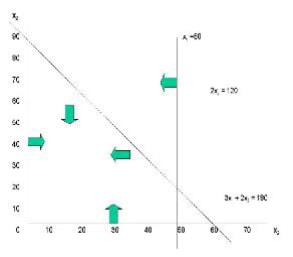
Then determine area of feasible study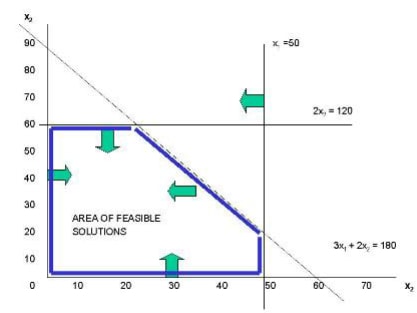
Note;
- The area under the line marked blue is the needed area or area of feasible solutions.
- We therefore shade the unwanted region out the trapezium marked blue
Optimization
List all corners (identify the corresponding coordinates), and pick the best in terms of the resulting value of the objective function.
- x1 = 0 x2 = 0 R = 30 (0) + 50 (0) = 0
- x1 = 50 x2 = 0 R = 30 (50) + 50 (0) = 1 500
- x1 = 0 x2 = 60 R = 30 (0) + 50 (60) = 3000
- x1 = 20 x2 = 60 R = 30 (20) + 50 (60) = 3600 (the optimal solution)
- x1 = 50 x2 = 1 5 R = 30 (50) + 50 (15) = 2250

Past KCSE Questions on the Topic.
- A school has to take 384 people for a tour. There are two types of buses available, type X and type Y. Type X can carry 64 passengers and type Y can carry 48 passengers. They have to use at least 7 buses.
- Form all the linear inequalities which will represent the above information.
- On the grid [provide, draw the inequalities and shade the unwanted region.
- The charges for hiring the buses are
Type X: Ksh 25,000
Type Y Ksh 20,000
Use your graph to determine the number of buses of each type that should be hired to minimize the cost.
- An institute offers two types of courses technical and business courses. The institute has a capacity of 500 students. There must be more business students than technical students but at least 200 students must take technical courses. Let x represent the number of technical students and y the number of business students.
- Write down three inequalities that describe the given conditions
- On the grid provided, draw the three inequalities
- If the institute makes a profit of Kshs 2, 500 to train one technical students and Kshs 1 ,000 to train one business student, determine
- The number of students that must be enrolled in each course to maximize the profit
- The maximum profit.
- A draper is required to supply two types of shirts A and type B. The total number of shirts must not be more than 400. He has to supply more type A than of type B however the number of types A shirts must be more than 300 and the number of type B shirts not be less than 80. Let x be the number of type A shirts and y be the number of types B shirts.
- Write down in terms of x and y all the linear inequalities representing the information above.
- On the grid provided, draw the inequalities and shade the unwanted regions
- The profits were as follows
Type A: Kshs 600 per shirt
Type B: Kshs 400 per shirt- Use the graph to determine the number of shirts of each type that should be made to maximize the profit.
- Calculate the maximum possible profit.
- A diet expert makes up a food production for sale by mixing two ingredients N and S. One kilogram of N contains 25 units of protein and 30 units of vitamins. One kilogram of S contains 50 units of protein and 45 units of vitamins. The food is sold in small bags each containing at least 175 units of protein and at least 1 80 units of vitamins. The mass of the food product in each bag must not exceed 6kg. If one bag of the mixture contains x kg of N and y kg of S
- Write down all the inequalities, in terms of x and representing the information above (2 marks)
- On the grid provided draw the inequalities by shading the unwanted regions (2 marks)
- If one kilogram of N costs Kshs 20 and one kilogram of S costs Kshs 50, use the graph to determine the lowest cost of one bag of the mixture.
- Esha flying company operates a flying service. It has two types of aeroplanes. The smaller one uses 180 litres of fuel per hour while the bigger one uses 300 litres per hour. The fuel available per week is 18,000 litres. The company is allowed 80 flying hours per week.
- Write down all the inequalities representing the above information
- On the grid provided on page 21 , draw all the inequalities in (a) above by shading the unwanted regions
- The profits on the smaller aeroplane is Kshs 4000 per hour while that on the bigger one is Kshs. 6000 per hour. Use your graph to determine the maximum profit that the company made per week.
- A company is considering installing two types of machines. A and B. The information about each type of machine is given in the table below.
The company decided to install x machines of types A and y machines of type BMachine Number of operators Floor space Daily profit A 2 5m2 Kshs 1,500 B 5 8m2 Kshs 2,500 - Write down the inequalities that express the following conditions
- he number of operators available is 40
- The floor space available is 80m2
- The company is to install not less than 3 type of A machine
- The number of type B machines must be more than one third the number of type A machines
- On the grid provided, draw the inequalities in part (a) above and shade the unwanted region.
- Draw a search line and use it to determine the number of machines of each type that should be installed to maximize the daily profit
- Write down the inequalities that express the following conditions
Download Linear Programming - Mathematics Form 4 Notes.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

