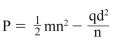Kenya Certificate Of Secondary Education(KCSE 2013) Mathematics Alt Paper 2A with Marking Scheme

SECTION I (50 marks)
Answer all the questions in this section in the spaces provided.

1. The sum of n terms of the sequence; 3, 9, 15, 21… is 7500. Determine the value of n. (3 marks)
2. A quadratic curve passes through the points (-2, 0) and (1, 0). Find the equation of the curve in the form y = ax² + bx+ c, where a, b and c are constants. (2 marks)
3. Make d the subject of the formula.
   
4. Solve the equation
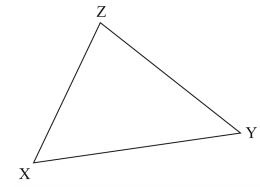
   2 log x – log (x – 2) = 2 log 3. (3 marks)
   
   1. Using a pair of compasses and a ruler only, construct an escribed circle to touch sides XZ of triangle XYZ drawn below. (3 marks)
      
   2. Measure the radius of the circle. (1 mark)
5. The equation of a circle is given by x² + 4x + y² – 4 = 0. Determine the centre and the radius of the circle. (3 marks)
   
   1. Expand (1- x)⁵ (1 mark)
   2. Use the expansion in (a) up to the term x³ to approximate the value of (0.98)⁵. (2 marks)
6. The position vectors of points F, G and H are f, g and h respectively. Point H divides FG in the ratio 4:-1, Express h in terms of f and g. (2 marks)
7. Two machines M and N produce 60% and 40% respectively of the total number of items manufactured in a factory. It is observed that 5% of the items produced by machine M are defective while 3% of the products produced by machine N are defective. If an item is selected at random from the factory, find the probability that it is defective. (3 marks)
8. Two taps A and B can fill an empty tank in 3 hours and 2 hours respectively. A drainage tap R can empty the full tank in 6 hours. Taps A and R are opened for 5 hours then closed.
   
   1. Determine the fraction of the tank that is still empty. (2 marks)
   2. Find how long it would take to fill the remaining fraction of the tank if all the three taps are opened. (2 marks)
9. Simplify the expression , leaving the answer in the form a√b+c where a, b and c are integers.(3 marks)
10. A point P moves inside a sector of a circle, centre O, and chord AB such that 2 cm < OP ≤ 3 cm and angle APB = 65⁰. Draw the locus of P. (4 marks)
11. The table below shows the taxes income for a certain year. 
    
    In that year, a monthly personal tax relief of Ksh 1 056 was allowed. Calculate the monthly income tax paid by an employee who earned a monthly salary of Ksh 32 500. (4 marks)
12. Solve the equation 6 cos²x + 7 sin x – 8 = 0 for 0⁰ ≤ x ≤ 90⁰. (4 marks)
13. The positions of two towns are (2⁰S, 30⁰E) and (2⁰S, 37. 4⁰E). Calculate, to the nearest km, the shortest distance between the two towns. (Take the radius of the earth to be 6370 km) (2 marks)
14. The vertices of a triangle T are A(1, 2), B(4, 2) and C(3, 4). The vertices of triangle T', the image of T are A'(¹/₂, 1), B'(2, 1) and C'(³/₂,2).
    Determine the transformation matrix M = (^a_c ^b_d) that maps T onto T'. (3 marks)

SECTION II (50 marks)
Answer only five questions from this section in the spaces provided.

17. The Hire Purchase(H.P.) price of a public address system was Ksh 276 000. A deposit of Ksh 60 000 was paid followed by 18 monthly instalments. The cash price of the public address system was 10% less than the H.P price.
    
    1. Calculate:
       1. The monthly instalment; (2 marks)
       2. The cash price. (2 marks)
    2. A customer decided to buy the system in cash and was allowed a 5% discount on the cash price. He took a bank loan to buy the system in cash. The bank charged compound interest on the loan at the rate of 20% p.a . The loan was repaid 2 years. Calculate the amount repaid to the bank at the end of the second year.(3 marks)
    3. Express as a percentage of the Hire Purchase price, the difference between the amount repaid to the bank and the Hire Purchase Price. (3 marks)
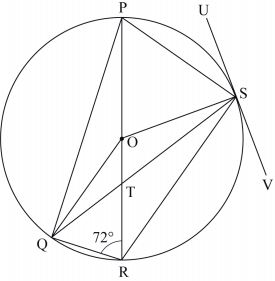
18. In the figure below, PR is the diameter of the circle centre O. Points P, Q, R and S are on the circumference of the circle. Angle PRQ = 72⁰, QS = QP and the line USV is the tangent to the circle at S. 
    
    
    Giving reasons, calculate the size of:
    1. ∠ QPR; (2 marks)
    2. ∠PQS; (2 marks)
    3. ∠ OQS; (2 marks)
    4. ∠RTS; (2 marks)
    5. ∠RSV. (2 marks)
19.  
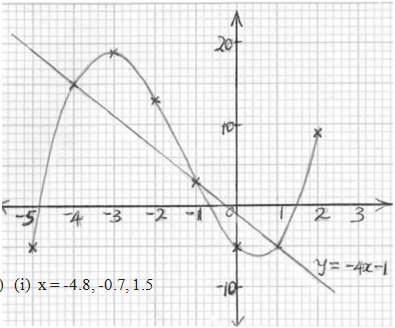
    1. Complete the table below for y = x³ + 4x² – 5x – 5. (2 marks)
       
    2. On the grid provided, draw the graph of y = x³ + 4x² – 5x – 5 for – 5 ≤ x ≤2. ( 3 marks)
    3. 1. Use the graph to solve the equation x³ + 4x² – 5x – 5 = 0. (2 marks)
       2. By drawing a suitable straight line graph, solve the equation
          x³ + 4x² – 5x - 5 = - 4x – 1. (3 marks)
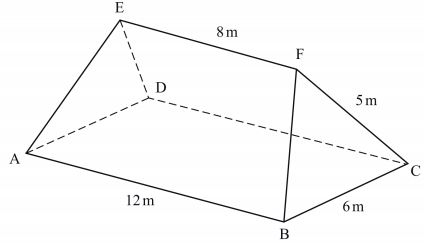
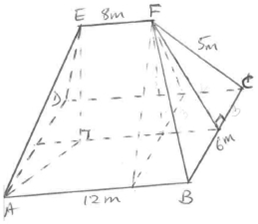
20. The figure ABCDEF below represents a roof of a house. AB = DC = 12m, BC = AD = 6m, AE = BF= CF = DE= 5m and EF = 8m.
    
    
    
    1. Calculate, correct to 2 decimal places, the perpendicular distance of EF from the plane ABCD. (3 marks)
    2. Calculate the angle between:
       1. The planes ADE and ABCD; (2 marks)
       2. The line AE and the plane ABCD, correct to one decimal place; (2 marks)
       3. The planes ABFE and DCFE, correct to 1 decimal place. (3 marks)
21.  
    1. Complete the table below, giving the values correct to one decimal place. (2 marks)
       
    2. On the grid provided, using the same scale and axes, draw the graphs of y= 2 sin (x+20)⁰ and y= √3 cos⁡ x for 0° ≤ x ≤ 240°. (5 marks)
    3. Use the graphs drawn in (b) above to determine:
       1. the values of x for which 2 sin⁡ (x+20)= √3 cos ⁡x;  (2 marks)
       2. the difference in the amplitudes of y=2 sin⁡(x+20)and y= √3 cos ⁡x. (1 mark)
22. Three quantities R, S and T are such that R varies directly as S and inversely as the square of T.
    1. Given that R = 480 when S = 150 and T = 5, write an equation connecting R, S and T. (4 marks)
    2. 1. Find the value of S when R = 360 and T = 1.5. (2 marks)
       2. Find the percentage change in R if S is increased by 5% and T decreased by 20%. (4 marks)
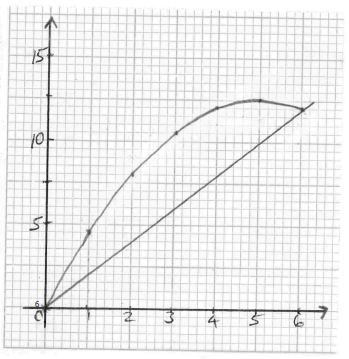
23. The equation of a curve is given by y = 5x- ¹/₂ x².
    1. On the grid provided, draw the curve of y = 5x- ¹/₂ x² for 0 ≤ x ≤ 6. (3 marks)
    2. By integration, find the area bounded by the curve, the line x=6 and the x-axis. (3 marks)
    3.  
       1. On the same grid as in (a), draw the line y = 2x. (1 mark)
       2. Determine the area bounded by the curve and the line y = 2x. (3 marks)
24. The table below shows marks scored by 42 students in a test.
    
    
    
    1. Starting with the mark of 25 and using equal class intervals of 10, make a frequency distribution table. (2 marks)
    2. On the grid provided, draw the ogive for the data. (4 marks)
    3. Using the graph in (b) above, estimate:
       1. The median mark; (2 marks)
       2. The upper quartile mark. (2 marks)

MARKING SCHEME

1	1st term, a = 3; common difference, d = 6 7500 =n/2 2# 3 + (n - 1) x 6, 3n2 = 7500 n = √2500 = 50	B1 M1 A1 3
2	y = (x + 2)(x - 1) y = x2 + x - 2	M1 A1 2
3	P = ½mn2 -qd 2 x n                    n pn =½mn3 - qd2 q          q       q pn =  mn 3 - d2  q        2q √d2 = √mn3 - qn             2q       q d = √mn3 - pn          2q      q  d = √½mn3 - pn               q	B1 M1 A1 3
4	Log c (x - 2) m = log 3 x2- 2 = 9 x2 - 9x + 18 = 0 (x - 6)(x - 3) = 0 x = 6 or x = 3	M1 M1 A1 3
5	radius = 3.1	B1 B1 B1 B1  4	extending YX and YZ bisecting +s VXZ and XZW escribed circle drawn allow ± 0.1
6	Completing square on L.H.S. x2 + 4x + 4 + y2 - 2y + 1 = 4 + 4 + 1 (x + 2)2 + ( y - 1)2 = 9 centre of circle : (-2, 1) radius of circle: 3 units 4	B1 B1 B1 3
7	(1 - x)5 = 1 + 5(-x) + 10(-x)2 + 10(-x)3 + 5(-x)4 + (-x)5 = 1 - 5x + 10x2 - 10x3 + 5x4 - x5 (0.98)5 = (1 - 0.02)5 & x = 0.02 (0.98)5 = 1 - 5(0.02)5 + 10(0.02)3 - 10(0.02)3 = 1 - 0.1 + 0.004 - 0.00008 = 0.90392	B1 M1 A1 3
8	- 1               4 n+ = 4 + (- 1) f+ + 4 + (- 1) g+     - 1 +4  =   f+    g+	M1 A1 2
9	P(defective) : M" 0.6 x 0.05 = 0.03 N " 0.4 x 0.03 = 0.012 P(defective) 0.03 + 0.02 = 0.042	M1 M1 A1 3	For 0.6 # 0.05 or 0.4 # 0.03 0.95 good M 0.6 0.05 defective 0.4 0.97 good N 0.03 defective
10	Fraction filled if A and R are open for 5h = 5     6 Fraction of tank still empty = 1 - = 5  1                                                     6  6 Fraction filled if A, B and R are open for 1h 1 + 1 = 1 - 2  3    2    6    3 Time taken to fill the tank =¼ h or 15 min	B1 B1 M1 A1 4
11	√48 =  4,35 - 3h √5 + √35 + 3h5 - 3 h = 4,35 - 3 h         5 - 3 = 2 √35 - √3 h = 2 √15 - 6	M1 M1 A1 3
12	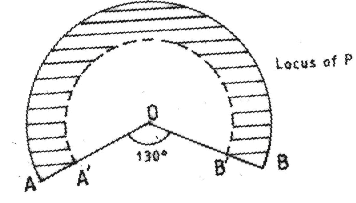+AOB = 130c arc AB - solid curve arc A´B´ - broken curve region shown	B1 B1 B1 B1 4
13	9680 x 0.1 = 968 9120 x 0.15; 9120 x 0.2; 4580 x 0.25 = 1368      = 1824             = 1145 Net tax = (968 + 1368 + 1824 +1145) - 1056 = 4249	M1 M1 M1 A1 4
14	6(1 - sin2x) + 7 sin x - 8 = 0 6 - 6 sin2x + 7 sin x - 8 = 0 6 sin2x - 7 sin x + 2 = 0 (3 sin x - 2) (2 sin x - 1) = 0 2 1 sin x = 2/3 or sin x = ½ x = 41.81° or x = 30°	M1 M1 M1 A1 4
15	Distance between towns K and S = 2π # 6370 cos 2° x 37.4 - 30                                     360 = 822.2121281 = 822 km	M1 A1 2
16		M1 M1 A1 3	:formation and solution of simultaneous equations : formation and solution of simultaneous equations
17	276000 - 60000        18 = 12 000 276000 x 0.9 = 248400 248400 x 0.95 = 235980 235980 x 1.22 = 339811.2 339811.2 - 276000 63811.2 x 100 276000 = 23.12 %	M1 A1 M1 A1 M1 M1 A1 M1 M1 A1 10
18	+QPR = 90° - 72° = 18° +PQR = 90° - angle subtended by diameter +PQS = 180° - 2(72) = 36° +PSQ = 72° - angle subtended at the circumference by chord PQ equal and base +’s of isosceles ∆QPS = 72° +OQS = 36° - 18° = 18° base angles of isosceles ∆ OPQ = 18° +RTS = 180 - (36 + 18) = 126° extension angle RTS equal to sum of opposite interior angles TSP and TPS +RSV = 90° - 36° = 54° +RSV = +RPS - angle in alternate segment.	B1 B1 B1 B1 B1 B1 B1 B1 B1 B1 or equivalent 10
19	x -5 -4 -3 -2 -1 0 1 2 y = x3 + 4x2 - 2x - 2 -5 15   13 3   -5 9            x = -4.8, -0.7, 1.5 y = -4x - 1 Solutions x = -4, -1, 1.	B2 S1 P1 C1 B2 P1 L1 B1 10	allow B1 for 4 correct Suitable scale All correctly plotted ±0.1 allow B1 for 2 values : plotting for line
20	= distance of EF from place ABCD slant height from F to BC = 52 - 32 =4 ` = distance of EF from plane ABCD 2 2 = 42 - 22 = √12 = 3.46 m       angle between planes ADE and ABCD = tan-1 12             2 = 60° angle between line AE and plane ABCD = sin-1 12             5 = 43.9° angle between planes ABFE and DCFE = 2 tan-1 3      c      √12 m = 81.8°	M1 M1 A1 M1 A1 M1 A1 M1 M1 A1 10	or equivalent or equivalent -1 3 tan or equivalent 12 doubling
21	x  0 40 80 120 160 200 240 y = 2sinx + 20   1.7   1.3   -1.3   y = √3cos x     0.3   -1.6   -0.9             2 sin (x + 20) = 3 cos x x = 30° and x = 210° amplitude difference 2 - 1.7 = 0.3	B1 B1 S1 P1 P1 C1 C1 B1 B1 B1 10	suitable scale used plotting 2 Sin (x + 20) plotting 3 cos x curve for 2 sin x + 20 curve for √3 cos x
22	R = 480 whe n S = 150 and T = 5 480 =k x 150             52  =150k     25 =480 x 25 = 80      150 R = 80S     80 x 360 R = (1.5)2 = 80 x 360        2.25 = 12800 S2 = 1.05s, T2 = 0.8T R2 = 80 x 1.05S             (0.8T) = 80 x 1.05 S         (0.8)  R2 = 131.25  = 64.0625 = 64.06 %	B1 M1 A1 B1 M1 A1 B1 M1 M1 A1 10
23	x  0 1 2 3 4 5 6 y = 5x - ½x2 0 4.5 8 10.5 12 12.5 12             Drawing line y = 2x Area of ∆ : ½ x 6 x 12 = 36 Bounded area = 54 - 36 = 18	B1 P1 C1 M1 M1 A1 L1 M1 A1 B1 10	table may be implied : plotting : curve : integral : substitution
24	Marks Frequency cf 25-34 4 4 35-44 5 9 45-54 8 17 55-64 12 29 65-74 9 38 75-84 3 41 cfs       Identification of median = 57.5 ± 0.5 Identification of upper quartile mark = 66.5 ± 0.5	B1 B1 B1 S1 P1 C1 B1 B1 B1 B1 10	: marks class column : frequency column : scale : plotting : curve